选择适当的材料(本构)模型和材料常数通常是建模中最重要也是最困难的部分 。就非线性材料而言,材料模型复杂和不容易理解,其性质更不容易得到,通过参照文献来发现材料数据可能很困难,故需要进行专门的材料测试,而很多时候试验条件的限制,无法进行完备且有效的试验。本文从简易例子入手,采用ANSYS workbench+OptiSLang进行材料的参数识别,可有效解决材料参数的确定性问题,在此基础上,可以进行其他复杂的参数识别(比如LS-DYNA中的 Mat 145,参数繁杂,不易测得),故本例仅作为一种思路。
情况1.单调递增

图1
情况2:滞回曲线

图2
此时的将加载和卸载分解,分别作为参考(reference),注意最大荷载和卸载时与横轴交点
情况3:同时有材料的两种曲线(比如混凝土受拉和受压等 )
弹簧钢因预先施加的位移而变形

图3 红线为试验值,作为参考reference,先选择一组数据作为初始参数(蓝线)进行计算

图4 变形云图
材料模型选用非线性各向同性硬化(nliso)

图5
ansys帮助文档对该模型有详细的解释

确定材料参数以最佳地适合该材料力-位移曲线的测量值
未知参数为:E,屈服强度,线性强化系数,指数强化系数,指数饱和度参数

达到min目标函数是参考曲线和计算曲线(力 - 位移)函数值之间的平方差的总和

图6 本例敏感性分析链

图7 输入参数

图8 双击parameters set进行查看

图9 位移加载

图10 fixed约束

图11 u1和u2

图12 提取支反力位置

图13 提取reference

图14 提取simulation(可调取时程文件file.rst)

图15 为了获得相同的长度和离散化,有必要从Ref中提取横坐标,并将Sim内插到该横坐标,optislang有丰富的函数形式,本例用到interpolate(simulation,disp_ref,liner,0,0)

图16 p11为目标函数

图17 各参数控制范围,同时也可设置其他辅助项控制,比如曲线的斜率不小于0

图18 开始敏感性分析
线性强化系数R0对结果影响很小,为非重要参数,这是因为线性强化系数R0为曲线的斜率(图5),在本例中趋于0(图21)
图21

图22 Direct optimization
图23 优化结果,绿线为试验参考线,红线为优化结果,从图中可以看到,模拟值与试验值有非常好的一致性,再进行后处理就可以得到最佳设计点的参数。
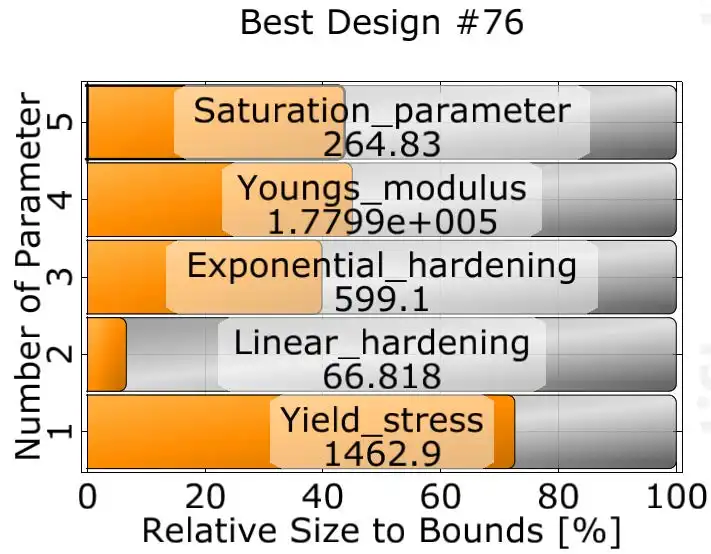
图24 参数
当然利用Mechanial APDL也可以进行此次参数识别,先编写好命令流,使用Workbench 的Mechanial APDL模块,读取命令流文件,计算分析并存储力-位移,调取,敏感性分析,优化,原理类似。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删