1.前言
本文旨在解释利用Adams/Vibration模块进行动总解耦分析的计算原理,并通过计算程序实现与Adams/Vibration的相互验证。尝试解释解耦计算过程中出现的情况,如贡献量为负值、总和大于100等现象。
已有不少参考文献对其进行解释,本文主要引用文献3中的数据及术语,最终的计算结果虽不能与此文献相对应,但是也能够与Adams/Vibration互相验证。
此文若存在不合理之处,欢迎讨论。
2.计算原理
动总的刚体模态及解耦率计算,实质是计算一个质量+多个弹簧的多自由度系统,通过列出微分方程,求解特征值(频率),特征向量(振型),并将特征向量按照自由度划分为6个方向,计算每个方向的模态能量贡献量(即解耦率)。
微分方程[2,3,4]: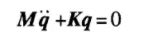
其中:
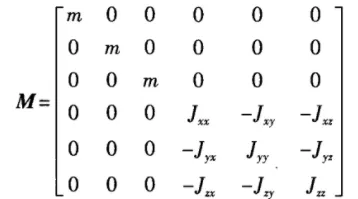
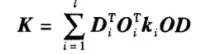 ,Di为悬置位置转换矩阵,Oi为悬置方向转换矩阵,ki为悬置三向刚度矩阵。
,Di为悬置位置转换矩阵,Oi为悬置方向转换矩阵,ki为悬置三向刚度矩阵。
由定义可知:,即矩阵的特征值,频率f=sqrt(λ)/2/pi。
至此,可求出系统的固有频率及振型。
模态贡献量,此处也是模态动能的贡献量。第n阶的最大模态动能,可表示为
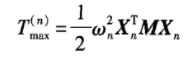 ,将其按照自由度分为6个方向,每个方向的动能为:
,将其按照自由度分为6个方向,每个方向的动能为:
3个平动方向: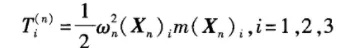
3个转动方向:

模态贡献量即各个自由度分量占最大值的比例。通过上述可得到6X6的模态能量贡献矩阵,称为基于自由度的模态能量分布矩阵,即一般Matlab的计算方法。
Adams/Vibration中,将模态能量分成9个方向,其中3个平动方向与前述一致,将前述中的三个转动方向,分为纯与Jxx、Jyy、Jzz相关的三个及纯与Jxy、Jyz、Jzx相关的三个量[1]。
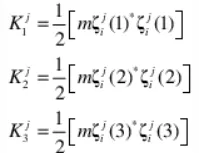
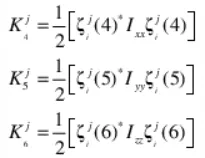
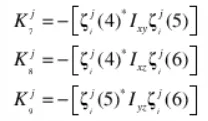
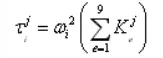
综上,两者的任意阶的模态动能总量是相同的,两者方法只是将总量分成了6份或者9份的区别,通过公示可以进行相互转换。
Adams/Vibration中由于单独考虑Jxy、Jyz、Jzx的影响,更容易出现贡献量是负值的情况,属于正常计算结果,若是考虑负值,总和为100%。
3.具体算例
输入参数:
表1 悬置软垫3向静刚度(N/mm)
| 方向 | 左前悬置 | 右前悬置 | 左后悬置 | 右后悬置 |
| u | 138.75 | 138.75 | 11.25 | 11.25 |
| v | 185 | 185 | 18 | 18 |
| w | 1110 | 1110 | 90 | 90 |
表2 总成质量与惯量
| M/kg | Jxx/Kg.m2 | Jyy/Kg.m2 | Jzz/Kg.m2 | Jxy/Kg.m2 | Jyz/Kg.m2 | Jzx/Kg.m2 |
| 238.7 | 12.46 | 22.79 | 19.63 | 0.40 | 0.50 | 1.20 |
表3 悬置软垫安装位置(mm)
| 坐标 | 左前悬置 | 右前悬置 | 左后悬置 | 右后悬置 |
| u | 102 | 54 | -644.7 | -644.7 |
| v | -204.6 | 226.5 | -124.1 | 145.9 |
| w | -132.6 | -132.6 | -192.9 | -192.9 |
计算结果:
(1)频率计算结果
表4 频率计算结果对比
| 单位-Hz | 1 | 2 | 3 | 4 | 5 | 6 |
| M文件计算结果 | 5.39 | 6.14 | 6.44 | 10.16 | 15.42 | 16.17 |
| Adams/Vibration计算结果 | 5.39 | 6.14 | 6.44 | 10.15 | 15.40 | 16.17 |
通过Matlab求解特征值并求得频率的方法,与Adams/Vibration计算结果基本一致,误差<0.2%。
(2)贡献量计算结果
表4 基于惯性参数的能量计算结果对比
| M文件计算结果 | Adams/Vibration计算结果 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| X | 95.64 | 0.08 | 0.66 | 3.60 | 0.02 | 0.00 | 95.59 | 0.08 | 0.67 | 3.63 | 0.02 | 0 |
| Y | 0.06 | 52.53 | 45.36 | 0.36 | 1.44 | 0.25 | 0.06 | 52.65 | 45.22 | 0.36 | 1.46 | 0.24 |
| Z | 0.03 | 0.01 | 0.00 | 1.83 | 15.84 | 82.29 | 0.03 | 0.01 | 0 | 1.84 | 15.14 | 82.98 |
| Rxx | 0.04 | 0.90 | 0.99 | 1.99 | 79.58 | 17.17 | 0.04 | 0.91 | 0.99 | 1.99 | 80.27 | 16.46 |
| Ryy | 3.50 | 0.22 | 0.00 | 91.56 | 4.55 | 0.28 | 3.53 | 0.22 | 0 | 91.51 | 4.54 | 0.31 |
| Rzz | 0.76 | 47.08 | 51.87 | 0.10 | 0.73 | 0.12 | 0.77 | 46.95 | 51.99 | 0.10 | 0.74 | 0.11 |
| Rxy | 0.02 | 0.02 | 0.00 | 0.64 | -0.90 | 0.10 | 0.02 | 0.02 | 0 | 0.64 | -0.91 | 0.11 |
| Ryz | 0.03 | -1.00 | 1.10 | 0.07 | -1.17 | -0.22 | 0.03 | -1.01 | 1 | 0.07 | -1.19 | -0.21 |
| Rzx | -0.08 | 0.15 | 0.02 | -0.14 | -0.09 | 0.01 | -0.08 | 0.15 | 0.02 | -0.14 | -0.09 | 0.11 |
通过Matlab求解9个分量的贡献量并与Adams/Vibration进行对比,计算结果基本一致,贡献量>10%的数据中,误差最大的出现在6阶的Rxx,为4.1%,略大。
此表中可以看到出现负值属于正常的计算结果,若是将所有贡献量都按绝对值相加,便会出现大于100%的现象。
表5 基于自由度的VS基于惯性参数的能量计算结果对比
| M文件计算结果-基于惯性参数的(6X9) | M文件计算结果-基于自由度的(6X6) | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| X | 95.64 | 0.08 | 0.66 | 3.60 | 0.02 | 0.00 | 95.64 | 0.08 | 0.66 | 3.60 | 0.02 | 0.00 | |
| Y | 0.06 | 52.53 | 45.36 | 0.36 | 1.44 | 0.25 | 0.06 | 52.53 | 45.36 | 0.36 | 1.44 | 0.25 | |
| Z | 0.03 | 0.01 | 0.00 | 1.83 | 15.84 | 82.29 | 0.03 | 0.01 | 0.00 | 1.83 | 15.84 | 82.29 | |
| Rxx | 0.04 | 0.90 | 0.99 | 1.99 | 79.58 | 17.17 | 0.06 | 0.41 | 1.53 | 2.34 | 78.54 | 17.11 | |
| Ryy | 3.50 | 0.22 | 0.00 | 91.56 | 4.55 | 0.28 | 3.47 | 0.31 | 0.01 | 91.81 | 4.06 | 0.34 | |
| Rzz | 0.76 | 47.08 | 51.87 | 0.10 | 0.73 | 0.12 | 0.74 | 46.66 | 52.43 | 0.06 | 0.10 | 0.01 | |
| Rxy | 0.02 | 0.02 | 0.00 | 0.64 | -0.90 | 0.10 | - | - | - | - | - | - | |
| Ryz | 0.03 | -1.00 | 1.10 | 0.07 | -1.17 | -0.22 | - | - | - | - | - | - | |
| Rzx | -0.08 | 0.15 | 0.02 | -0.14 | -0.09 | 0.01 | - | - | - | - | - | - | |
通过Matlab计算,将模态能量分为9个分量及6个分量,可以看出分成9个分量时,更易出现模态贡献量为负的情况。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删
武汉格发信息技术有限公司,格发许可优化管理系统可以帮你评估贵公司软件许可的真实需求,再低成本合规性管理软件许可,帮助贵司提高软件投资回报率,为软件采购、使用提供科学决策依据。支持的软件有: CAD,CAE,PDM,PLM,Catia,Ugnx, AutoCAD, Pro/E, Solidworks ,Hyperworks, Protel,CAXA,OpenWorks LandMark,MATLAB,Enovia,Winchill,TeamCenter,MathCAD,Ansys, Abaqus,ls-dyna, Fluent, MSC,Bentley,License,UG,ug,catia,Dassault Systèmes,AutoDesk,Altair,autocad,PTC,SolidWorks,Ansys,Siemens PLM Software,Paradigm,Mathworks,Borland,AVEVA,ESRI,hP,Solibri,Progman,Leica,Cadence,IBM,SIMULIA,Citrix,Sybase,Schlumberger,MSC Products...