Matlab实现沙漏游戏的编程技巧

这个和我们常说的“沙漏”还不是一回事儿。

不过我由此想到我自己以前做过的一个小的程序，一个沙漏游戏。

这个游戏中，并没有把砂看作连续介质，无需用连续介质的方法来模拟它。把每一个像素点看作一粒砂，砂动=像素点移动。

这个游戏中，我们可以自己定义沙漏的形状（黑色的是砂漏边界），沙漏中有两种颜色的砂，空白之处用白色表示。每一个计算步中，砂子一一定的概率向自己的左下、右下、下方移动，当然前提是那里是空格。

熟悉CA的朋友应该知道，这是一个简单的CA，规则十分简单。MATLAB代码也很简单，初学者都能看懂。如果有哪里写得不好，还请大家指正。

计算步增加可以类比时间的流逝，最终砂子会慢慢落下、在底部形成堆积体，下图是计算的中间结果。

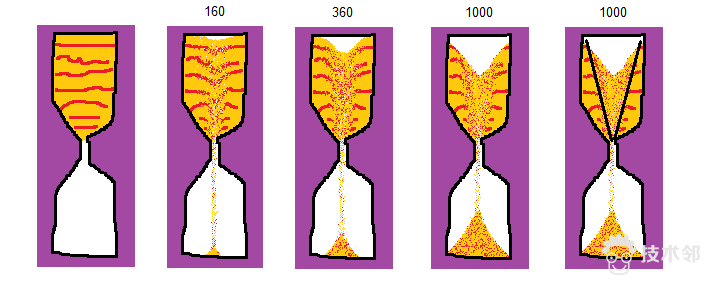
细心的读者可以发现，沙漏中砂下落时，首先下落的是中心部分的，第五张图中用两条黑线做了标记，黑线以外的砂在计算中一直没有动。当然，如果计算步足够多，它们也是会落下的。这和试验中观察到的现象非常一致：

由此可见，简单地规则，可以在一定程度上反映物体的运动规律。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删