产品
梁尺寸为：长270mm，宽25mm，厚1mm。
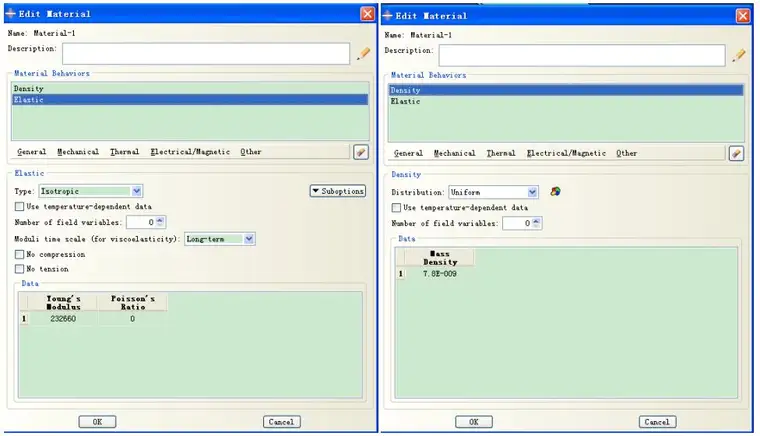
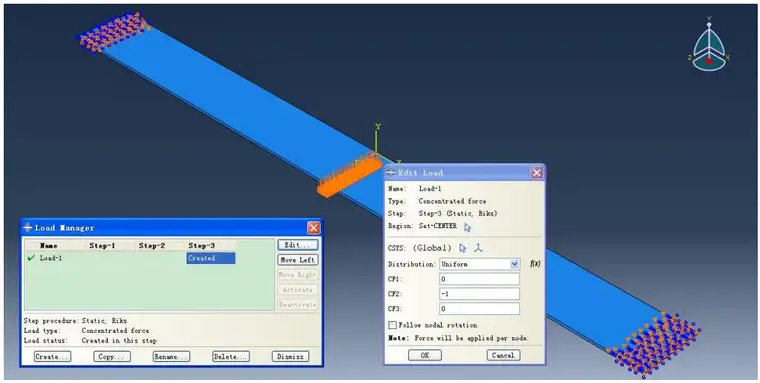
第一分析步中，限制梁两端节点只能沿梁轴线方向滑动，同时给梁中部节点一个向上的微小位移，这里定为0.1mm；第二步里，给梁两端的节点一个相对的位移，均为0.75mm，以模拟梁的压缩状态；第三步里，分析步选用非线性屈曲分析，在第二步的基础上，给中部节点施加一个向下的力，定为1.
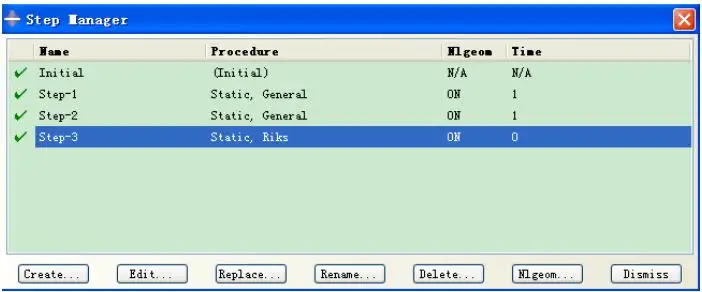
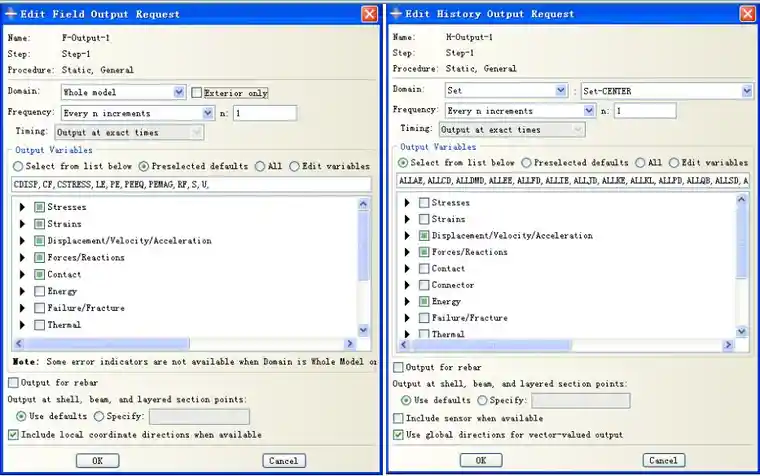
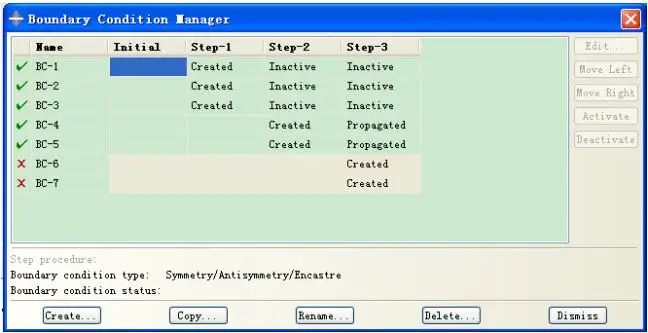
载荷的加载与分析步相对应，BC-1和BC-2为固定梁两端五个自由度，仅保留水平方向自由度，BC-3为给垂向一个位移0.1mm；BC-3和BC-4为给梁两端一个0.75mm的位移；在第二分析步中已经令梁两端有了一个相对位移，默认到达移动位置后固定，因此BC-6和BC-7为冗余约束，此处作了无效处理。
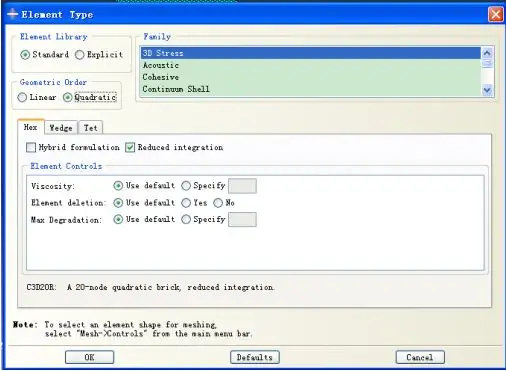
选择二次单元
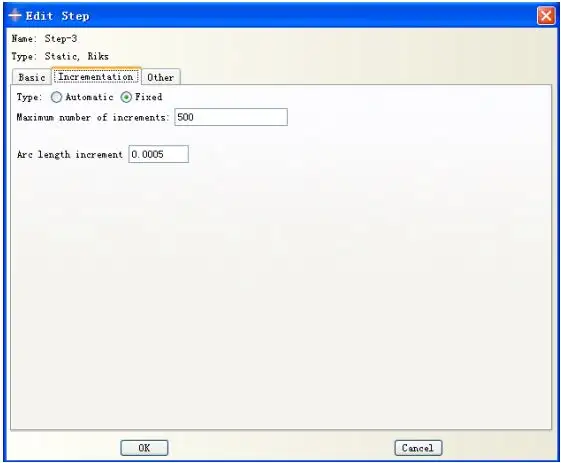
计算之前修改分析步第三步的步长为固定值0.0005，共500步，如图所示。
两端均压缩0.75mm后梁的变形为：
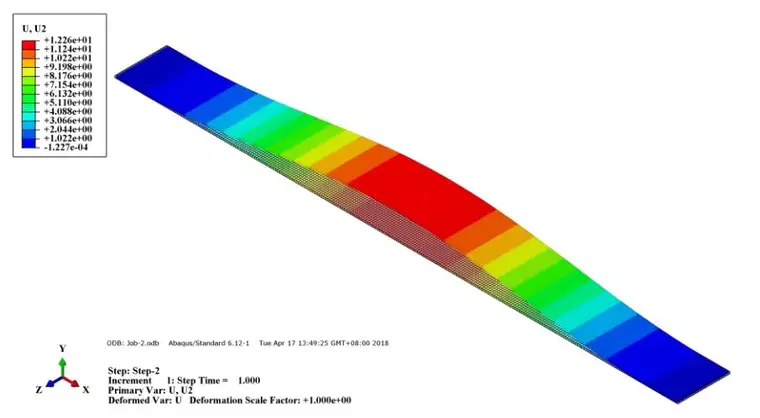
中部加载前梁的应力分布云图
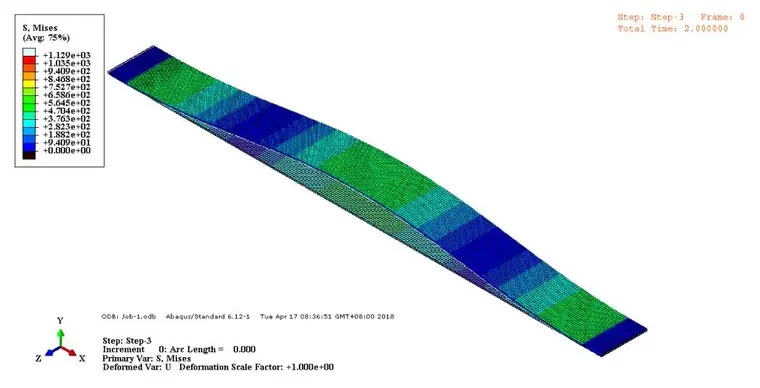
加载后梁的应力分布云图：
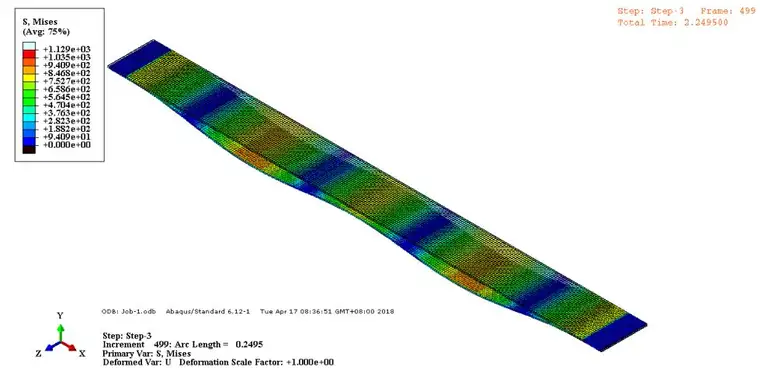
将数据导出，在MATLAB中绘图，得到力位移曲线：
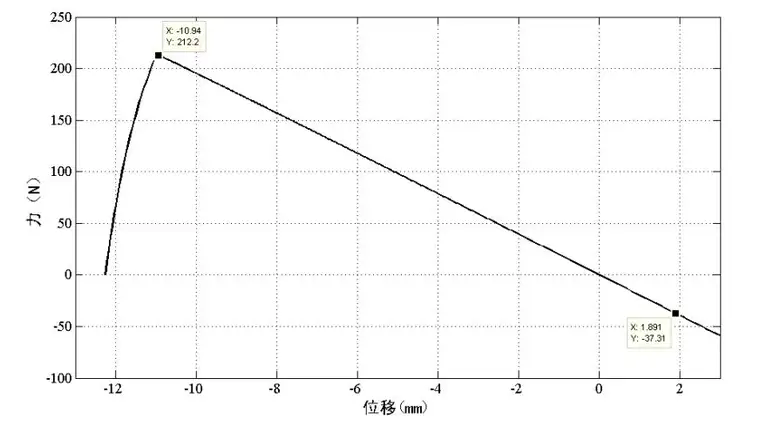
由图中数据计算可知梁的负刚度为：
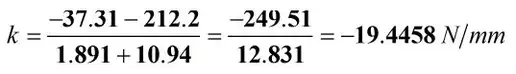
按柔性设计手册里的公式：
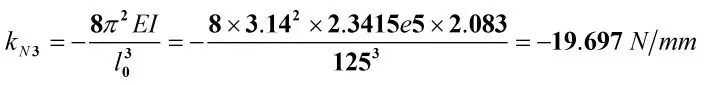
可见两者相差极小，可认为仿真结果有效。取上图局部放大，得到压力为0时梁的位移情况如下图所示。
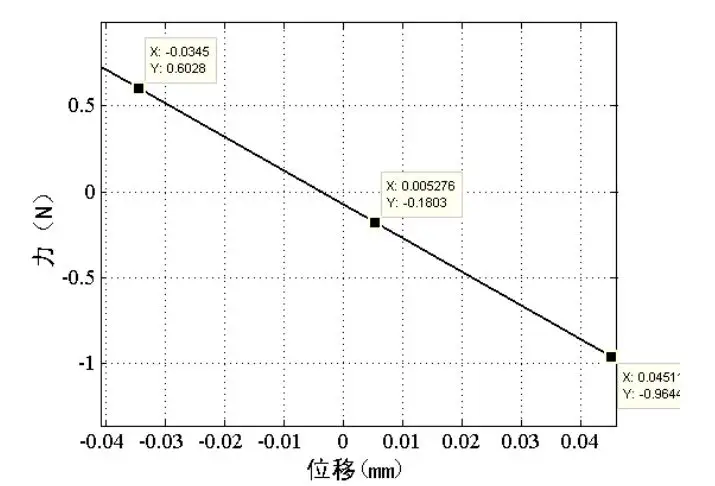
由于仿真计算采样点的限制且误差不可避免，通过上图可知，位移为0时，受力也为接近0。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
