计算成本:
显式(Explicit)分析中,基于单元的稳定极限(时间增量)可由下式计算:

在二维分析中,在每个方向上将网格加密为2倍,显式分析的运行时间增加4-8倍,初始时间增量大小减小一半。类似地,在三维分析中,在每个方向上网格加密为2倍将使运行时间增加16倍。在准静态分析(quasi-static analysis)中,通过加速模拟过程或缩放质量的方式来降低计算成本是很有效的。但是都应该监测动能,确保动能与内部能量的比值不会太大—通常需小于10%。
实例说明:
以二维平面应变管道贯入为例,说明Explicit中降低计算成本的通用方法:
1. 使用多线程和调整动态负载降低计算成本
在提交Job选项框里可启用多线程计算,所选线程数不能超过电脑CPU的实际线程数,一般不带超线程的CPU,建议不要将所有线程用于计算,否则电脑会卡顿,无法进行其他操作,保留1-2个线程比较稳妥。动态负载域的个数要大于等于线程数,一般采用默认值。


| 单线程 | 双线程 | 注 | |
| CPU Time (/s) | 577.5 | 314 | 多线程可明显减小计算时间,但线程数与计算时间不呈倍数关系 |
| 计算成本(/s) | 682 | 573 |
注意:在Monitor中显示的CPU Time并非实际计算所花费的时间,计算成本应该以Log文件中完成时间(Completed)与提交时间(Submitted)的差值为准,但CPU Time与计算成本呈正相关,故以CPU Time来衡量计算成本。
2. 加速模拟过程降低计算成本
为了减少所需的增量步数,n,可以加快模拟(相对于事件的实际时间),即人为地缩短事件的时间周期,但是这可能引发两个错误:
1) 如果模拟速度过快,增加的惯性力将严重影响之后的分析结果。避免该情况的唯一方法是适当的提速,不能过大。
2) 除了惯性力,其他因素,例如材料特性也可能与速率有关。在这种情况下,所模拟事件的实际时间不能更改。
这种方法很常见,例如在模拟贯入问题时,现场实际的时间可能是几个小时,贯入速度为几毫米每秒,而模拟时通常将分析时间设置为几秒或几分钟,来降低计算成本。
| Step time(/s) | 10 | 5 | 2.5 |
| 速度(mm/s) | 50 | 100 | 200 |
| CPU time(/s) | 38.4 | 26.6 | 19.3 |
注:此处使用了相同的多线程和质量缩放。
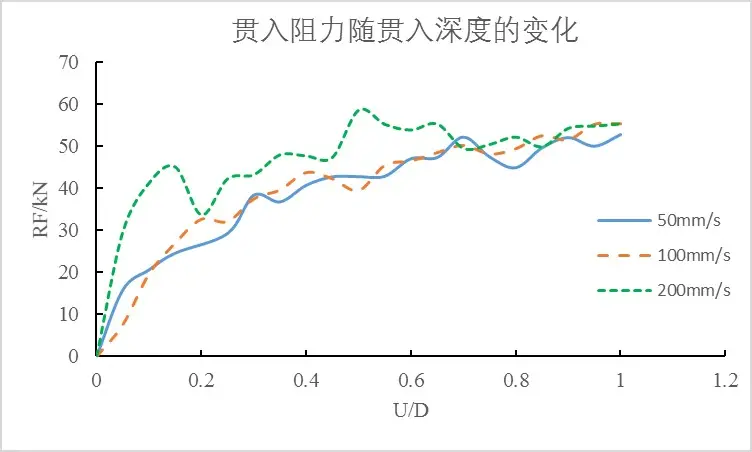
加速模拟过程降低计算成本效果显著,但是速度必须合适。
3. 质量缩放降低计算成本
人为地增加材料密度ρ,假定放大因子为f2,则增量步数由n降低到n/f,T降低到T/f,这个概念称为“质量缩放”。它降低了事件时间与波动在单元间传播的时间之比,同时使事件时间保持不变。这允许在分析中包含与速率相关的特性。但必须谨慎地使用,以确保惯性力不会对分析结果产生显著影响。质量缩放对惯性力的影响与加速模拟时间的方式相同。质量缩放可以通过改变密度来完成,但是ABAQUS中提供了更多的方法来缩放整个模型或模型中的特定单元集。
以下通过增大密度实现质量缩放:
| 质量缩放(f倍) | 无 | 10 | 100 |
| CPU time(/s) | 314 | 110.5 | 38.9 |
注:使用了双线程计算。


计算时间近似变为原来的1/sqrt(f)倍。放大倍数不能太大,否则计算结果将出现较大的偏差。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删