Abaqus热流固耦合分析：一维热固结问题探讨

当土壤承受负荷和温度变化时，必须解决一个描述变形，孔隙流体流动和通过土壤传热的方程组耦合问题，以准确预测固结行为。在这个问题中，说明了Abaqus / Standard对一维热固结建模的能力。研究了一维全饱和土在恒定表面载荷和恒定表面温度下的固结行为，并将所得结果与Aboustit等人的结果进行了比较。 （1985）。

问题描述

该问题可以视为与1.15.1节“ Terzaghi固结问题”的热学对应。该部分中的讨论同样适用于此问题，此处不再赘述。图1.15.6-1显示了线性弹性土柱在恒定表面压力和恒定表面温度下的一维热弹性固结。该列高7个单位，宽2个单位。土体底部受到约束，并且除允许自由流动的顶表面外，土体的所有侧面均不可渗透。顶表面承受1单位的恒定压力和50单位的恒定温度。假定土壤已完全饱和。重力被忽略了。 Aboustit等人报道的材料性能。 （1985）被使用。土壤是弹性的，模量为6000单位，泊松比为0.4。土壤的渗透率为4×10-6单位，比重为1单位。由于Aboustit等。 （1985年）只使用了一组热性质，对于固体和孔隙流体使用相同的热性质。比热为40单位，密度为1单位。土壤和孔隙流体的电导率为0.2单位，热膨胀系数为0.3×10-6。

One-dimensional thermal consolidation model.

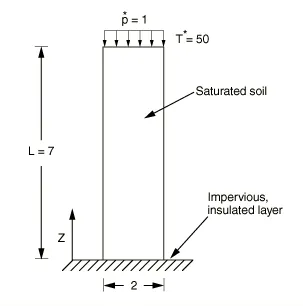
限制了所有垂直于侧面的位移以强制执行一维行为。固结分析使用具有自动时间步长的瞬态土固结步骤进行。此问题的时间步进由两个参数控制：一个参数控制温度场时间积分的准确性，另一个参数控制孔隙流体流时间积分的准确性。孔隙流体溶液的稳定性极限为

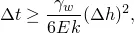
它规定了最小时间增量。该方程式中使用的变量在《 Abaqus Analysis用户指南》第6.8.1节“耦合的孔隙流体扩散和应力分析”中定义。所使用的网格与Aboustit等人使用的网格相同。 （1985），导致最小时间增量为0.1。由于施加了表面载荷，靠近表面的元件立即获得与施加的载荷相等的孔隙压力。因此，使用每增加1.1的最大孔隙压力变化以及初始时间增加0.1的情况。这样可确保在分析中不使用小于0.1的时间步长来满足孔隙流体流动的时间积分精度。选择最大允许温度变化增量为3，以避免必须使用小于所需孔隙流体稳定性极限的时间增量。通过首先仅使用最大孔隙压力变化的值运行问题并确定增量温度变化来获得最大允许温度变化的值。上面列出的参数值导致中等精度的解决方案。如果需要更精确的解决方案，则应使用更精细的网格。

由于负载量较小，因此非线性几何效应在此问题中并不重要。类似地，由于非常小的流体速度，由于孔隙流体流动而引起的热对流效果不足以支配不对称刚度。但是，出于完整性考虑，我们选择激活几何非线性分析以及不对称刚度。具有对称刚度的小应变分析的结果与给出的结果没有区别。该步骤的时间段为21.1，对应于将Abaqus / Standard结果与参考溶液进行比较的时间。

结果和讨论

在分析开始时，除顶表面外，整个区域的温度均为零，并且孔隙压力等于施加的表面载荷，因为所有载荷均由孔隙流体承担。随着时间的流逝，温度前沿从顶部到底部逐渐升高，并且随着孔隙流体从顶部流出，施加的表面载荷从孔隙流体转移到土壤骨架，从而降低了区域内的孔隙压力。在稳态极限下，所有区域的孔隙压力均为零，恒定温度等于施加的表面温度。在时间21.1，当温度前沿距顶表面已增加一定距离且孔隙压力部分降低时，比较孔隙压力和温度的Abaqus / Standard解决方案。结果如图1.15.6–2所示。使用施加的温度和施加的表面压力对温度和孔隙压力值进行归一化。纵坐标使用土柱的高度标准化。 Abaqus / Standard的结果与Aboustit等人的结果相当。 （1985）。

Normalized temperature and pore pressure along the z-direction at time 21.1.

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删