FLUENT在静态混合器中的数值模拟研究

1 前言

静态混合器是一种管道状的“在线”形式的“静态混合”设备。由于它本身就是管道状的，可以很方便地直接与工艺管道相连接，因而能够以“在线”的形式连续不断地进行混合作业。其所以称为“静态”，完全是为了突出它没有任何机械运转部件的特点，也是相对于以往带有各式各样搅拌装置的各种混合器而言的。在静态混合器的管道状外壳内，装有若干个长度较短的左旋和右旋的螺旋型结构。

一般每个螺旋元件的长度大约为螺旋元件外径（即管道内径）的1.5倍。左旋和右旋螺旋元件的叶片分别具有左旋和右旋180°的旋角。它们相互之间均呈现交替排列，而且每两个相互连接的左、右旋螺旋元件叶片的端部边缘均呈90°错角。一般将左、右旋螺旋元件各三个事先焊接在一起，再将它装入直径与之相应的标准管子内，就构成了静态混合器的一个标准组件。今天，我们做一个螺旋叶片式静态混合器的模拟案例。

2 建模与网格

管道为DN15标准管，外径φ20mm，壁厚1.5mm，因此内径为17mm。螺旋元件设计长度25.5mm，宽度16.5mm，元件壁厚1mm。静态混合器总长度127.5mm，因此螺旋元件共5个，故介质被切割的层数即分流数S=2⁵=32。

管道介质设计流量0.744m³/h，介质密度0.466kg/m³，动力粘度1.1927e-5Pa·s。建立如下静态混合器三维模型，采用fluent meshing模块划分多面体网格，节点数52万，最小网格正交质量0.08（本案例不纠结网格质量的提升）。CFD计算模型将混合器上下游增加了50mm的直管以减小计算的不稳定性，尤其是混合器出口可能会产生回流影响收敛性。

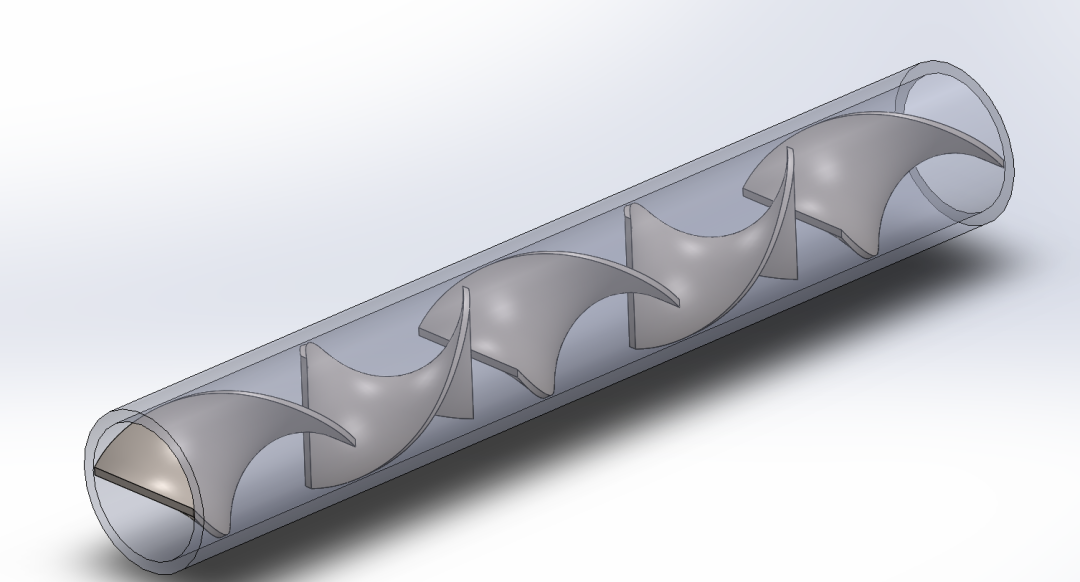
3 求解设置

根据上述条件，管道的流速为0.911m/s，雷诺数Re为1297.78，流动状态为层流。这是针对直管而言，若以混合器通流截面计算速度，以混合器叶片截面长度为特征长度计算的雷诺数也小于2000，因此可认为计算域内的流动状态为层流，故启用层流模型。

实际上也可尝试启用湍流模型，计算出的湍流强度也相当小，混合器的压降和层流模型计算的压降相差无几，也可以进一步说明流动状态。

为了验证混合器的混合效果，采用UDF定义入口温度分层边界，以简化模拟冷热流体的流入与混合，代码如下

#include "udf.h"DEFINE_PROFILE(MyProfile,thread,index){real x[ND_ND];real xx;face_t f;begin_f_loop(f,thread){F_CENTROID(x,f,thread);xx = x[0];if(xx<=-1.153956e-3)F_PROFILE(f,thread,index) =293.15;elseF_PROFILE(f,thread,index) =353.15;}end_f_loop(f,thread)}

其他设置默认，不做冗述，稳态求解。

4 计算结果

首先，我们看一下迭代残差曲线，可以看出收敛性还是相当好的，尽管网格质量不咋滴。

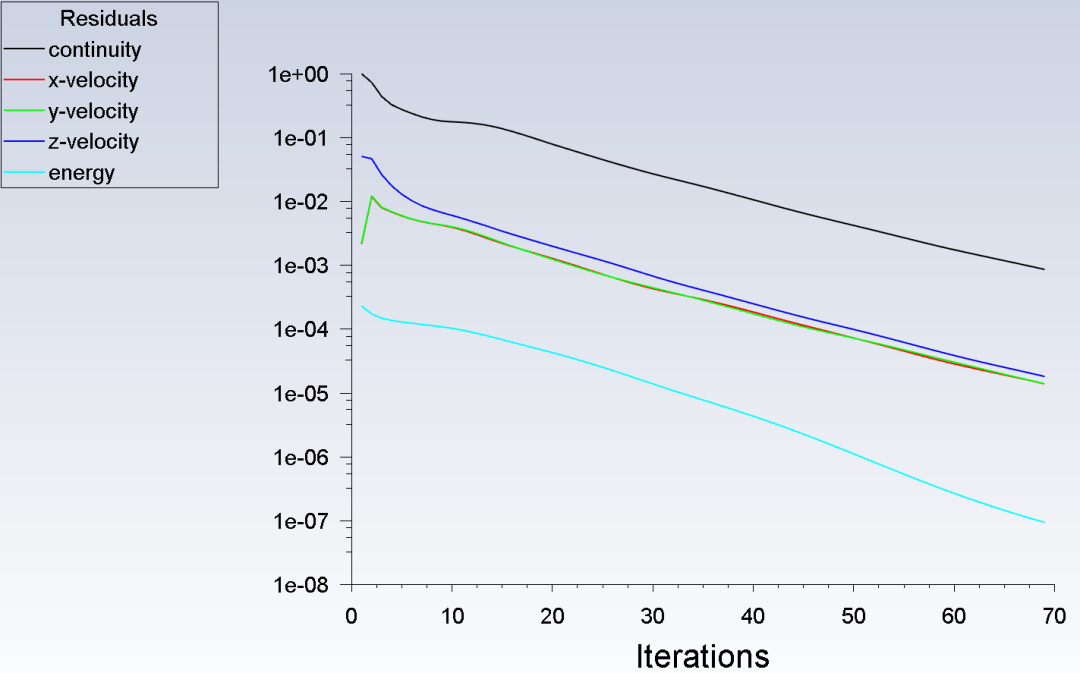
静态混合器的迹线如下，可以看出在螺旋原件区域管段介质进行了强烈的搅浑，介质除了管道轴向运动还有切向和径向运动，这是静态混合器的工作原理。

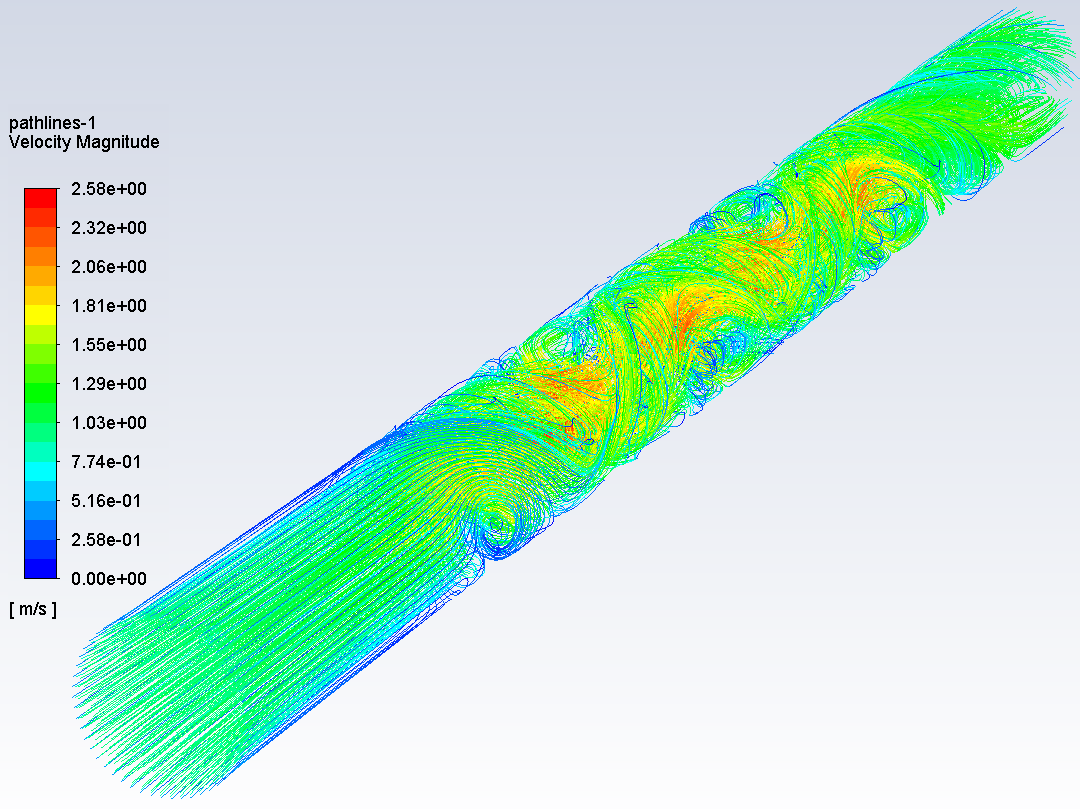
混合器的出口温度分布如下，可以看出冷热介质混合效果不错，最高温度43.79℃，最低温度42.6℃，相差约1.2℃（对于温度均匀性还可用不均匀系数来评价，本案例不进一步探讨了，感兴趣的读者可以查阅本号历史文章），注意到入口的最高温80℃，最低温度20℃。

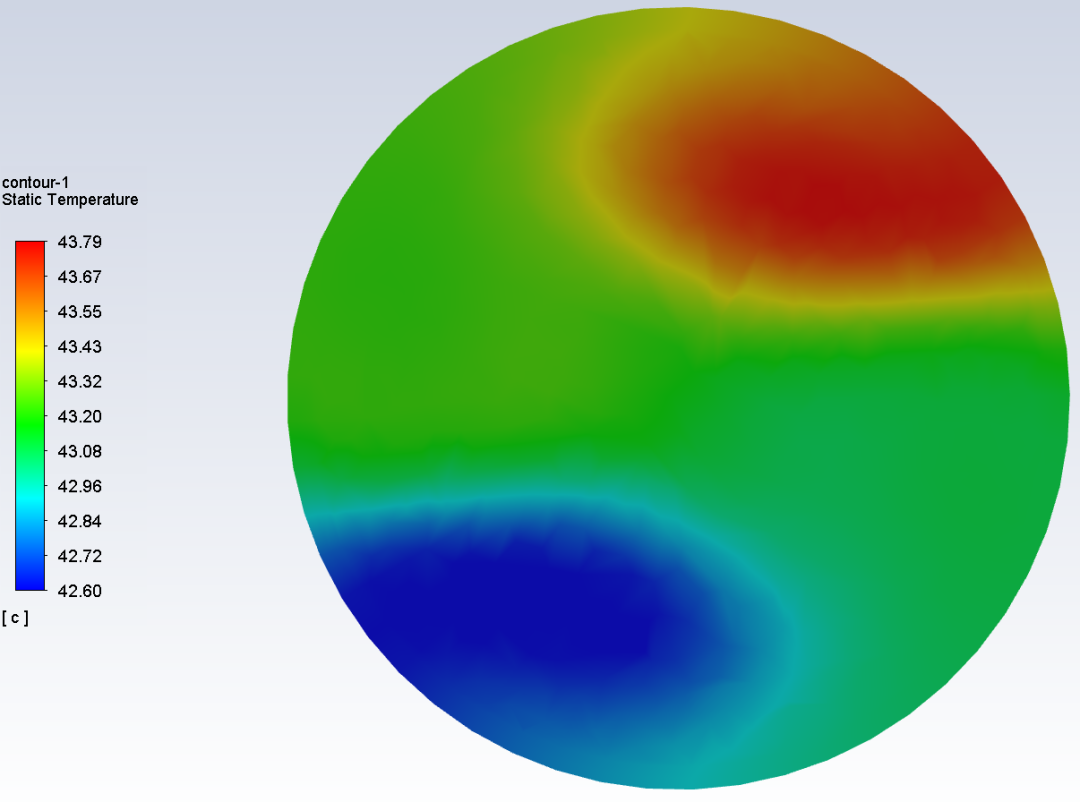
静态混合器的压降为4.41Pa。根据美国Kenics公司的资料，流体在与空管道等直接等长度的静态混合器中流动产生的压降，可以由流体在控管道中流动时的计算压降ΔP乘以一个系数Z来计算。

根据上述条件，管道的流速为0.911m/s，雷诺数Re为1297.78，流动状态为层流，摩擦系数f=0.0493，因此，等长度直管的流动压降ΔP=0.07Pa，Z=84.15（Z的求法如下），静态混合器的压力降为5.89Pa。

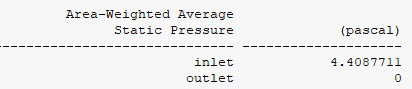
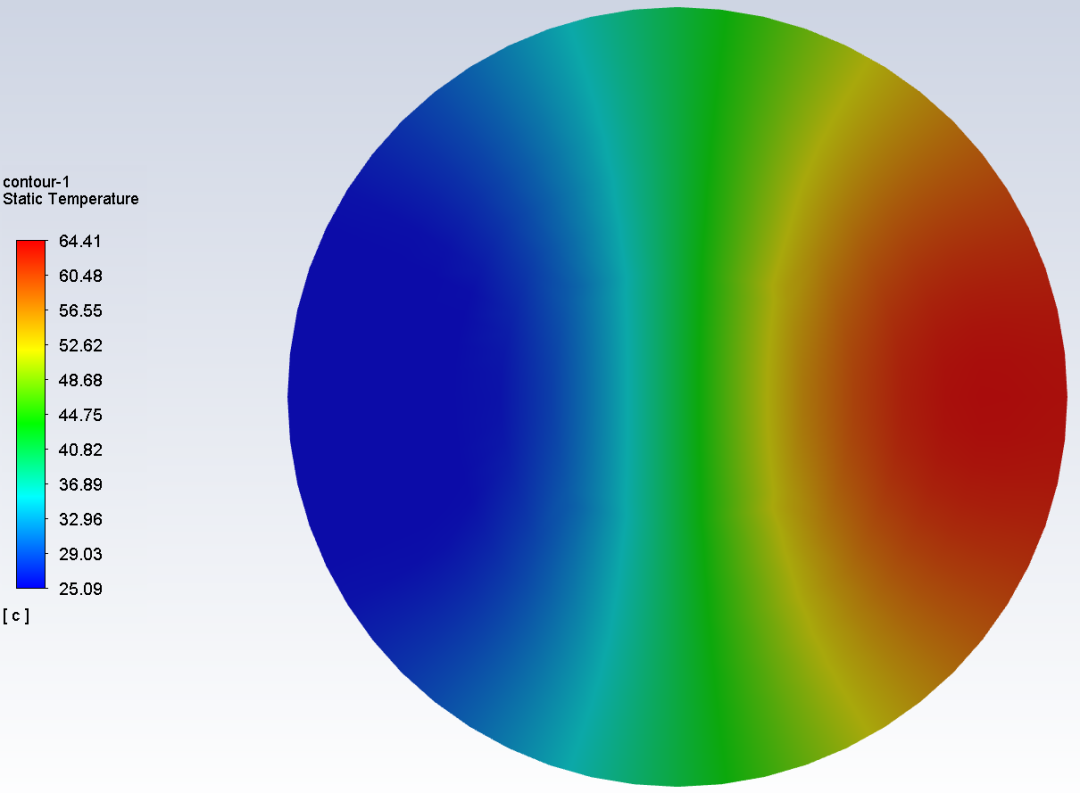
为了体现静态混合器的效果，建立等长度的直管道进行等边界条件计算，管道的迹线和出口温度分布如下，可以看出直管的流动温柔多了，出口温度还是那么有层次感，几乎没混合。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删