Abaqus弯曲残余应变偏小原因探析

我最近为一工程师校准了一个材料模型，他需要一个可以预测应力-应变响应和卸载后残余应变的材料模型。正如常见那样，材料参数所有实验测试都是在单轴拉伸下进行的。校准进行得很顺利，模型以高精度匹配所有数据（包括残余应变）。为了验证材料模型，然后使用它来预测弯曲实验中的响应，该实验主要关注残余变形。验证结果看起来却并不如预期。在本文中，我将尝试解释为什么在预测弯曲残余变形时需要特别小心。

材料模型

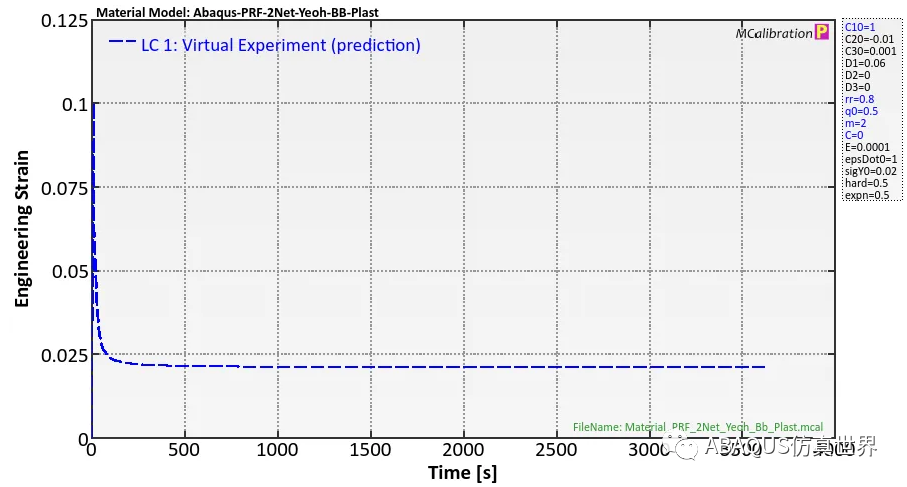
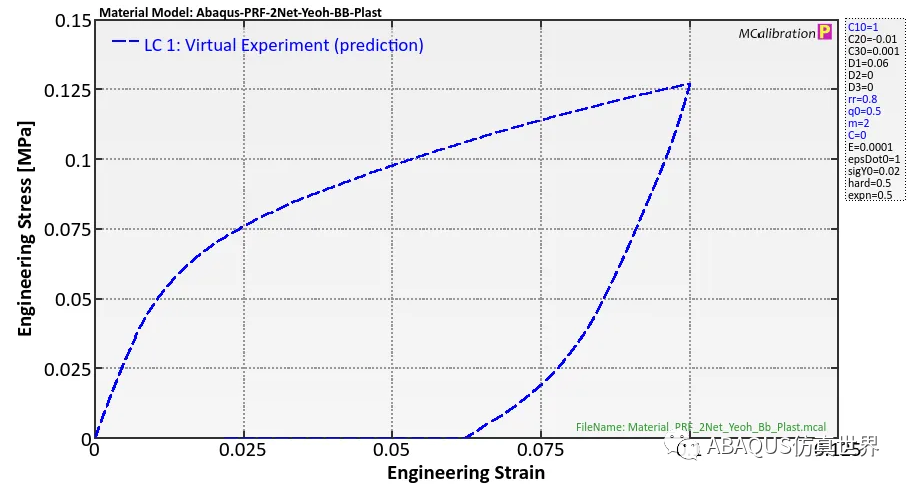
在此示例中，我将使用由 2 参数 Yeoh 模型、Bergstrom-Boyce 和各向同性硬化塑性组成的并行流变框架 (PRF) 模型。我没有特别的理由使用这个模型，只是它很容易使用。还有许多其他粘塑性材料模型会给出相同类型的结果。下图显示了虚拟载荷情况下的时间-应力-应变响应，其中材料被拉到 10% 的工程应变，然后卸载到零应力，然后在零应力下保持 1 小时。

模型 1：粗网格

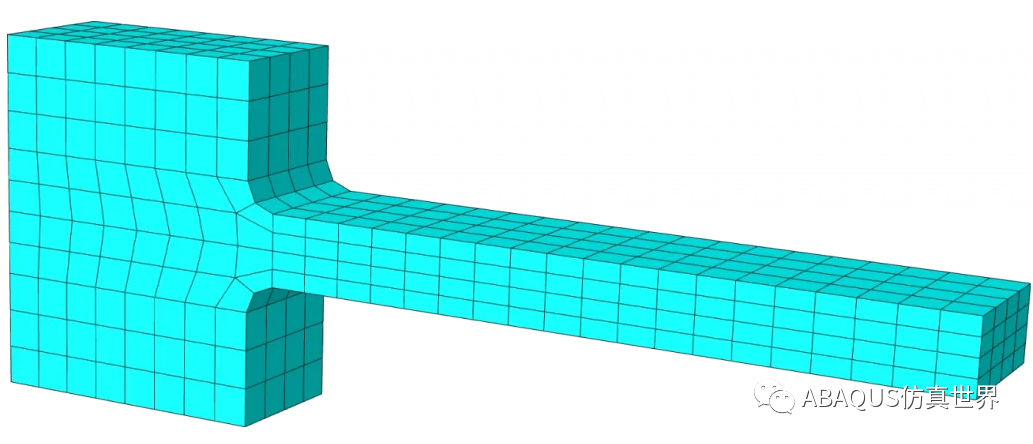
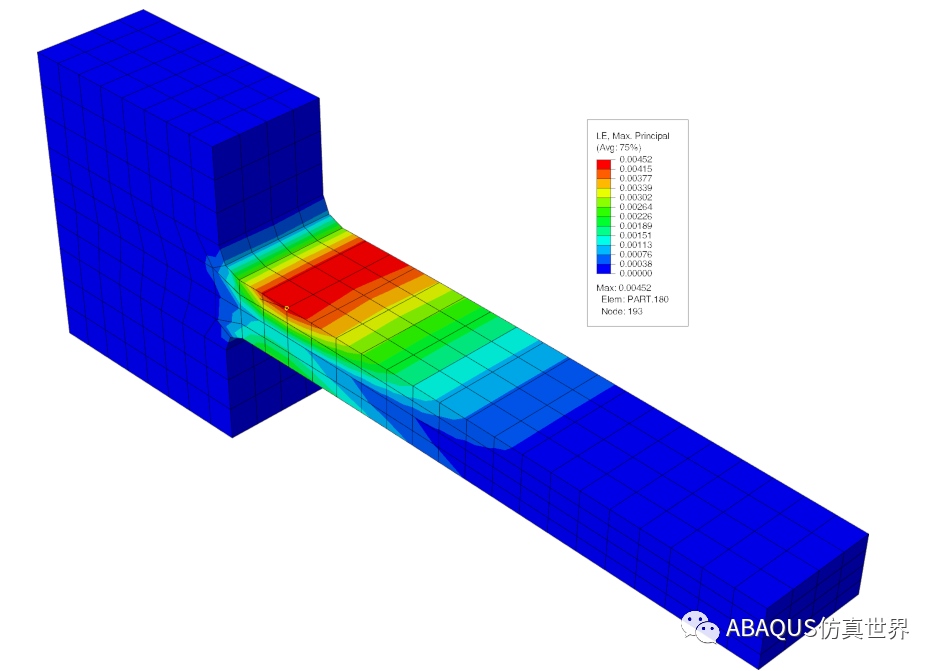
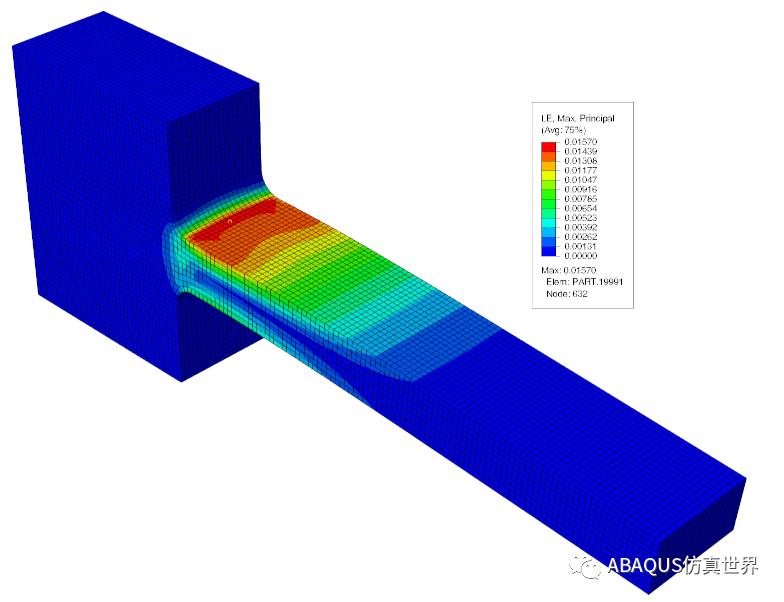
验证部件的左侧保持固定，并在部件的（右）尖端表面上施加向下的剪切牵引力（力）。尖端力的大小在 4 秒内逐渐增加，然后在另外 4 秒内逐渐移除，然后在没有任何外部负载的情况下放置 1 小时。该有限元模型使用 632 个线性缩减积分六面体单元 (Abaqus C3D8R)。下图显示了最大主残余应变。

模型 2：细网格

然后，我创建了包含更精细网格的模型：59,000 个线性全积分六面体单元。所有其他设置都相同。下图显示了最后 1 小时保持时间后预测的最大主应变。

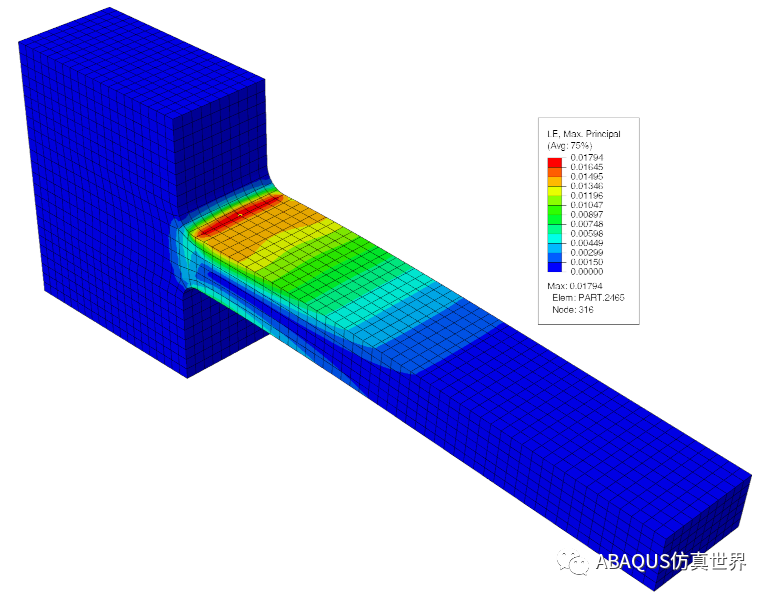
模型 3：精细网格（二阶单元）

第三个也是最后一个验证案例是使用 15,520 个完全积分二阶六面体单元 (Abaqus C3D20) 。所有其他设置都相同。下图显示了最后 1 小时保持时间后预测的最大主应变。

总结

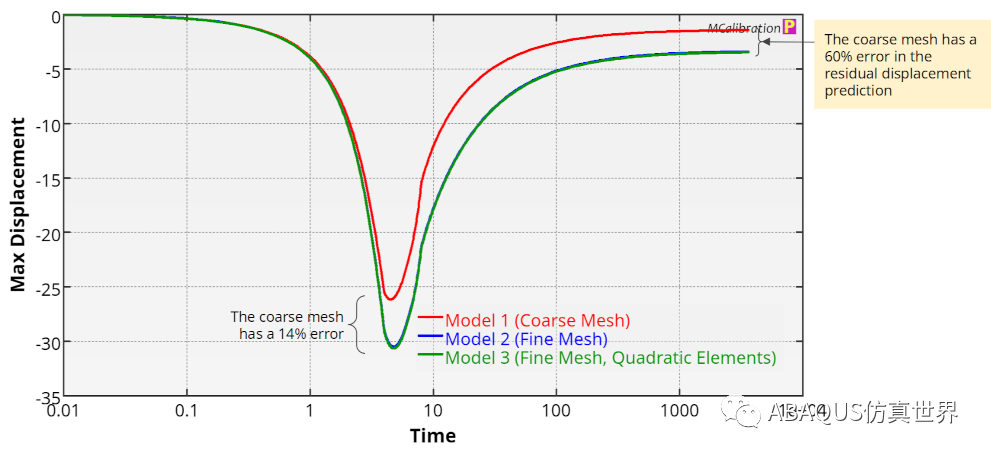
三个模型的结果给出了非常不同的最大残余主应变值。最粗的网格给出的最大主应变为 0.45%，最精细的网格预测为 1.79%， 是前者的 4 倍！比较不同模型的另一指标是考虑弯曲杆尖端的残余变形。下图显示3个模型尖端变形历史曲线。 三个模型之间最大变形相差只有大约 14% ，而 最终的残余变形却是完全不同的。粗网格模型预测的最终位移太小了 ， 存在60%的误差！这里的教训是，如果您希望准确预测弯曲中的残余应变或位移，使用非常精细的网格非常重要。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删