Abaqus解析：应力波传播与显式求解技术

今天也来说一说应力波的传播。应力传播顾名思义，是指应力在物体内部的传递。

举个简单栗子，如图1所示，我们研究有三个单元构成的杆在收到冲击载荷时瞬间的状态。载荷P作用在节点1，作为集中力的结果，施加在它上面。加速度导致节点 1 具有速度 ，而速度又会导致单元 1 中的应变率 。单元 1 中的应变增量是通过应变率的时间积分来获得的。

总应变 是初始应变 和应变增量之和。在这种情况下，初始应变为零。一旦计算了单元应变，就可以通过应用材料本构模型获得单元应力 。对于线弹性材料，应力只是弹性模量乘以总应变。这个过程如图 2 所示。节点 2 和 3 不会在第一个增量步中移动，因为没有对它们施加力。

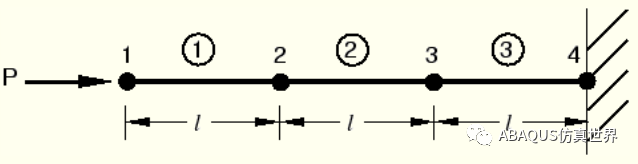
图1、在自由端施加载荷的杆初始状态

图2、在自由端施加载荷杆的增量步1 时刻的状态

在第二个增量中，单元 1 中的应力将内部单元力施加到与单元 1 相关的节点上，如图 3所示。然后使用这些单元应力计算节点 1 和 2 的动态平衡。该过程继续进行，因此在第三个增量开始时，单元 1 和单元 2 中均存在应力，节点 1、2 和 3 处存在力，如图 4 所示。该过程一直持续到分析最后时间。

图3、增量步2开始时的杆的状态

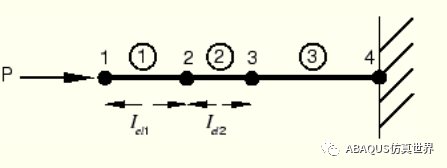
图4、增量 3 开始时的杆的状态

ABAQUS/Explicit 使用中心差分规则通过时间显式积分运动方程，使用一个增量的运动学条件来计算下一个增量的运动学条件。在增量开始时，程序求解动态平衡，其中指出节点质量矩阵 乘以节点加速度 等于总节点力（外作用力 和内部单元力 之间的差值）：

当前增量（时间）开始时的加速度计算如下：

由于显式过程总是使用对角线或集总质量矩阵，因此求解加速度是微不足道的；没有要求解的联立方程。任何节点的加速度完全由其质量和作用在其上的净力决定，因此节点计算非常高效。

使用中心差分规则对加速度进行时间积分，该规则在假定加速度恒定的情况下计算速度的变化。速度的这种变化被添加到从前一个增量中间开始的速度，以确定当前增量中间的速度：

速度在时间的积分并添加到增量开始时的位移以确定增量结束时的位移：

该方法在恒定加速度精确地积分。为产生准确结果，时间增量必须非常小，以便在增量期间加速度几乎恒定。由于时间增量必须很小，分析通常需要数万甚至几百万个增量步。幸运的是，每个增量都很高效，因为没有联立方程需要求解。大部分计算开销在于单元计算以确定作用在节点上的单元的内力。单元计算包括确定单元应变和应用材料本构关系（单元刚度）来确定单元应力，从而确定内力。
 

显式计算的优势

显式方法特别适合解决需要许多小增量才能获得高分辨率解决方案的高速动态事件。如果事件的持续时间很短，则可以有效解决。

接触条件和其他极不连续的事件很容易在显式方法中制定，并且可以在逐个节点的基础上强制执行而无需迭代。可以调整节点加速度以平衡接触过程中的外力和内力。显式方法最显着的特点是没有全局切线刚度矩阵，这是隐式方法所必需的。由于模型的状态是明确推进的，因此不需要迭代。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删