对于结构静力学中的简单线性问题,不需要对其设置,但是对于复杂的分析需要设置一些控制选项。分析设置是在Mechanical分析树的Static Structural下的Anslysis Settings细节设置中。
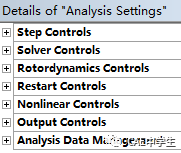
载荷步控制
求解器控制
转子动力学控制
重启控制
非线性控制
输出控制
分析数据管理
本文主要对载荷步控制、求解器控制、重启控制、非线性控制、输出控制、分析数据管理进行介绍。
载荷步控制用于指定求解步数和时间。在非线性分析时,用于控制时间步长。载荷步控制也用于创建多载荷步,如螺栓预紧载荷。
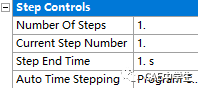
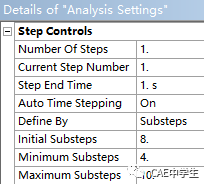
载荷步数:默认1
当前载荷步:默认1
载荷步结束时间:默认1s
自动步长时间:程序控制

自动步长时
间设置为ON
定义类型:子步/时间
初始子步:默认1
最小子步:默认1
最大子步:默认10
1.1 载荷步与子步
载荷步、子步和平衡迭代是控制加载求解过程的三个载荷时间历程节点。
1.1.1 载荷步
在线性静力学分析或稳态分析中,可以使用不同的载荷步施加不同的载荷组合。
在瞬态分析中,可以将多个载荷步加载到同一加载历程曲线的不同时间点。
注意:载荷可以分步,约束不能分步。
实例1,固定矩形条一端,在另一端分3步加载载荷,第一步只加载100N的力,第二步只加载10000Nm的逆时针扭矩,第三步推力与扭矩共同作用,求每一步的变形。
Step1,设置零件材料,接触关系,网格划分,过程略。
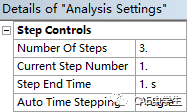
Step2,分析设置,将载荷步设置为3,其余默认。
Step3,设置边界条件,如下图。

载荷默认都是渐增(斜坡)加载的,用一个载荷步将载荷从0增加到设定值。
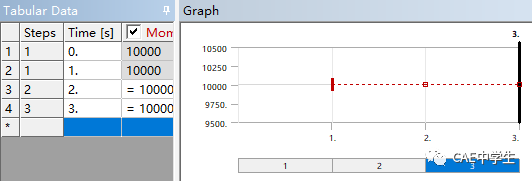
选中分析树中的Force,在信息窗口中出现了Tabular Data表格和Graph图表,代表了Force的加载历程,在第一步中,力从0渐变到100,并在第二三步中保持。
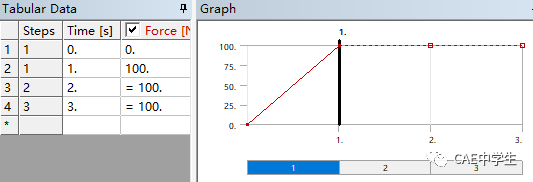
对于静力学分析,渐增加载与恒定加载计算无区别,本例将力与扭矩都改为恒定加载,在表格第一行将数字改为设定值。

要想Force在第二步不起作用,只需要点击图表的第二步区域或表格对应行,右击选择Activate/Deactive at this step!(在此步激活/取消),此载荷便在第二步中消失。
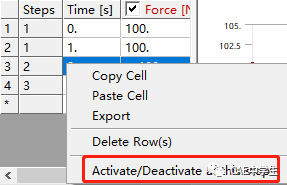
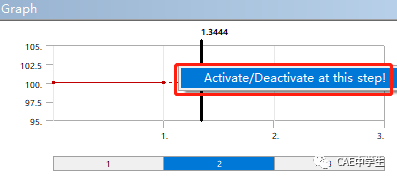
同样设置Moment载荷,使它在第一步中不起作用。
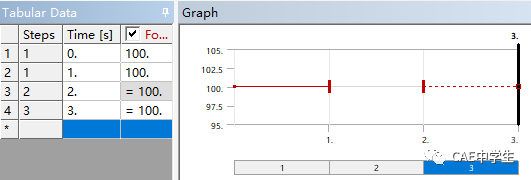
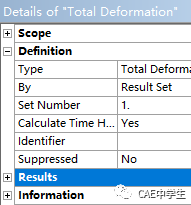
Step3,添加结果,点击分析树的Solution(A6),在工具栏出现Solution工具条,点击Deformation-Total(合位移),在分析树中便出现了Total Deformation项目,默认是最后结果,但是现在我们需要查看第一步结果。
在Total Deformation的细节设置中,By改为Result Set(结果位置),Set Number改为1,即表示第一步的结果。当然,也可以设置为Time(时间),然后在下一行Display Time改为1s。同样设置第二三步的结果。

Step4,计算,结果如下



实例2,螺栓预紧问题:螺栓预紧时,我们可以分两步加载预紧力,第一步坡度加载预紧力,第二步锁定。在分析设置中将载荷步设置为2。
选择Loads下的Bolt Pretension(螺栓预紧力),点击Graph图表的第一步,螺钉预紧力中Define By设置为Load,输入预紧力大小。再点击Graph图表的第二步,Define By设置为Lock锁定。

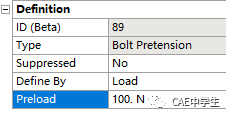
步1
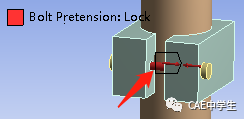
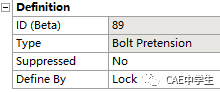
步2
1.1.2 子步
子步Substep是一个载荷步中插入若干的点。通常一个子步求解需要若干次迭代,每次迭代都被称为一次平衡迭代。子步对于求解过程的控制非常重要,很多时候需要使用不同的子步数来满足不同的加载和求解需要。子步的主要作用如下:
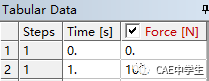
以下以矩形条一端固定一端加载力为例说明子步的设置方法

在分析设置中,将自动时间步Auto Time Stepping设置为On,Define By设置为Substep。然后需要设置三个参数
初始子步Initial substeps :用于计算初始加载量(即确定初始子步位置)。
最小子步Minimum Substeps,最大子步 Maximum Substeps用于计算子步之间的增量。三者关系数值关系必须满足:最小子步≤初始子步≤最大子步。大多数情况下,为了方便控制与计算,设置:最小子步=初始子步=最大子步。
比如给矩形条加载100N的力,载荷步为1,初始子步8,最小子步4,最大子步10。
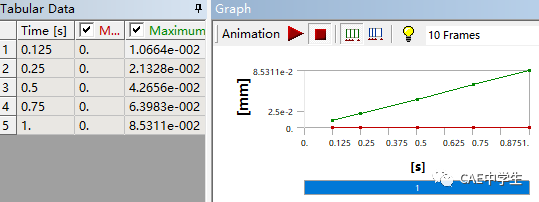
则力的初始加载值为 100N/8=25N,子步的数量为4~10(由程序选择),子步之间的增量范围为100N/10~100N/4,即10N~25N。其中最小子步不得大于最大子步,初始子步必须在最小子步和最大子步的数值之间)
计算后可以在图表中看到共生成了5个子步。
1.2 时间
载荷步和子步中经常会见到时间相关的选项,但是此处的1s不一定表示1s时间。无论载荷类型是否依赖于时间,Workbench都使用时间作为跟踪参数,这样,计算的结果将是与时间相关的函数。
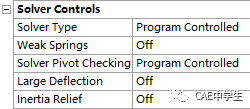
求解器类型:程序控制/直接/迭代
弱弹簧:程序控制/开/关
求解器主检查:程序控制/警告/错误/关
大变形:关(默认)/开
惯性释放:关(默认)/开
2.1 求解器类型
求解器类型有直接求解器Direct和迭代求解器Iterative。我们一般使用程序控制就可以。
直接求解器可以处理任何情况,主要用于薄面和细长体的模型。
迭代求解器在处理体积大的模型时很有效。
2.2 弱弹簧
弱弹簧Weak Springs:在某些时候,希望模型在平衡状态下计算,而不是约束所有方向,此时就会用到弱弹簧。比如如下一个几何体,在左右方向受到方向相反大小相等的力,理论上几何体处于平衡状态,不会发生刚体平移,但是在有限元软件中,经过网格离散化后,几何体可能处于微小的不平衡中,而弱弹簧就是用来平衡这种微小不平衡力。

但是,用户约束所有可能的刚体平移方向无意是更好的习惯,比如上图模型,可以采用1/2或1/4的模型,施加对称约束。
2.3 大变形
大变形Large Deflection用于几何非线性计算中,关于非线性的概念将在非线性分析一文中详解。大变形关闭时,计算器使用模型的初始刚度矩阵;大变形打开后,计算器将在每次迭代后重新生成刚度矩阵。
当变形超过5%或转角超过10°时,必须打开大变形开关。
2.4 惯性释放
通常在做静力学分析时,需要保证结构无刚体平移,否则求解器不能计算。但是在飞机飞行,轮船航行时要计算机构,需要采用惯性释放在结构上施加一个虚拟的约束反力,来保证合力平衡。惯性释放允许对完全无约束的结构进行静力分析。
3.1 重启控制
重启控制设置静力分析和瞬态分析中的多个重启点,来获得从某时刻重新启动分析所需的数据库。
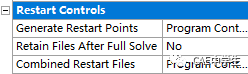
生成重启点:程序控制/手动/关闭
完成求解后保留文件:否/是
结合启动文件:程序控制/是/否
3.2 非线性控制
非线性控制可以修改收敛准则和其他一些求解控制选项,增加了稳定控制和稳定能量结果。
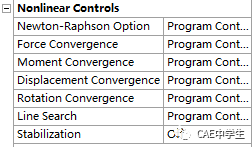
牛顿迭代法选项:程序控制/完整/修正/非对称
力收敛准则:程序控制/打开/移除
力矩收敛准则:程序控制/打开/移除
位移收敛准则:程序控制/打开/移除
转角收敛准则:程序控制/打开/移除
线性搜索:程序控制/打开/关闭
稳定性:关闭/常数/递减
3.3 输出控制
输出控制允许在结果后处理中得到需要的时间点结果,尤其在非线性分析中,中间载荷的结果也很重要。
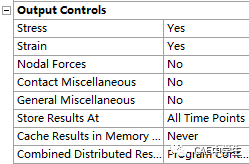
输出应力:是(默认)/否
输出应变:是(默认)/否
输出节点力:否(默认)/是
接触计算:否(默认)/是
通用计算:否(默认)/是
保存结果:所有时间点/最终/等距/指定重复
缓存到内存:从不/求解期间/依要求
合并分布式结果文件:程序控制/是/否
3.4 分析数据管理
分析数据管理用于管理分析数据的储存结果文件,以用于其他的分析系统。
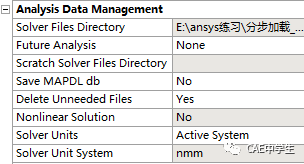
求解文件路径
后续分析类型:无/预应力分析/拓扑优化/预应力&拓扑优化
求解临时文件夹
保存MAPDL DB文件:否(默认)/是
删除不需要文件:是(默认)/否
删除非线性求解:否(默认)/是
求解器单位:当前激活的系统/手动
求解器单位系统:nmm
写在最后,除了在需要时设置载荷步与子步外,其余选项使用默认设置已经足以解决我们工作中的绝大部分需求。本文对不常用的设置只做了简单介绍,在以后的详细实例中还会根据具体需求讲解。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删