ANSYSHFSS求解选项深度解析：基函数阶数选择策略

A: 阶数的设置在工程树下的Analysis中选择setup，必须是advanced，如果是auto不可设置。

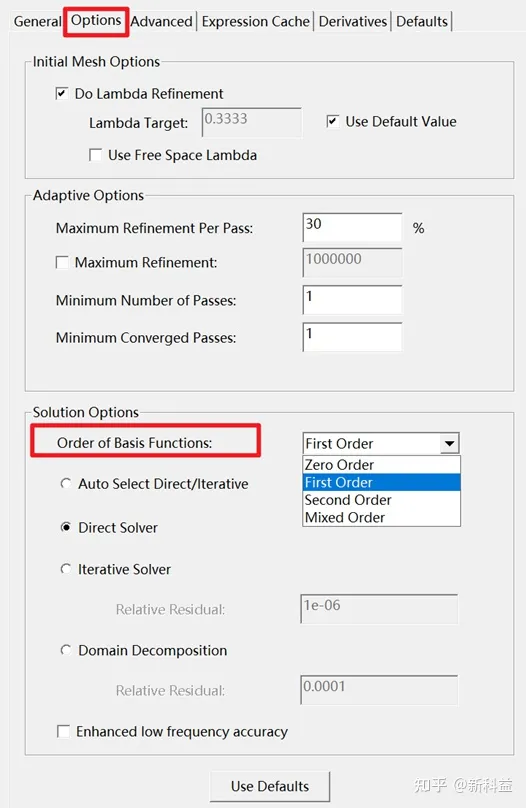
首先阶数决定每个网格单元内的场值插值策略；具体分为零阶，一阶，二阶和混合阶基函数：

• 零阶，节点值在顶点假设在四面体内域程线性变化，每个四面体6个未知数。

• 一阶，切向单元基函数对顶点和边上的场值进行插值每个四面体20个未知数。

• 二阶，切向单元基函数对顶点、边和面上的场值进行插值，每个四面体45个未知数。

• 混合阶，细化单元尺寸(h)的同时选择单元的阶数(p），生成最佳的基函数分级方案。

基函数阶数越高精确求解电场所需的四面体网格越少
– 更高阶的单元增加了精度
– 收敛度是基函数阶数的函数

下面以贴片天线为例展示他们的区别：
网格数量0阶比1阶多

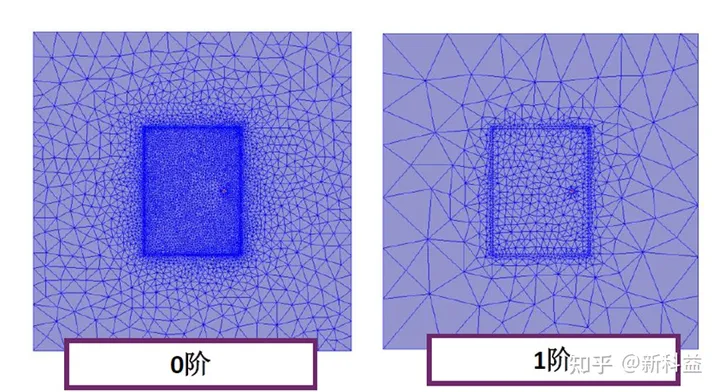
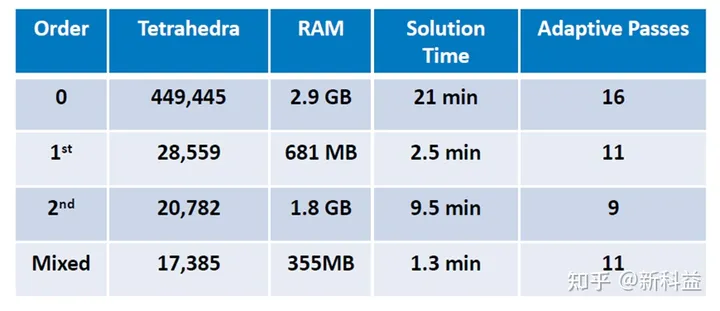
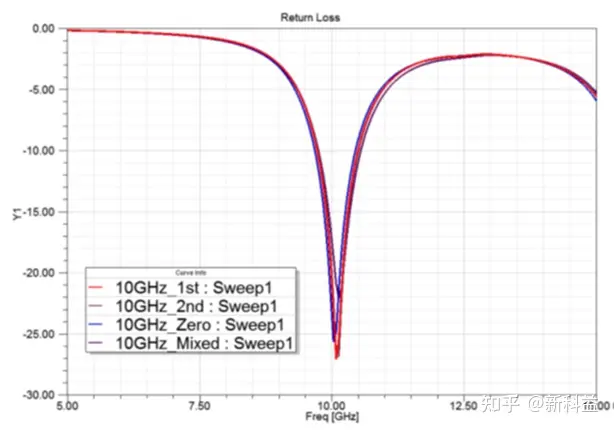
从上得出结论，采用各种基函数得到的仿真结果基本一致，混合阶的效率高、占用内存小。

B: 阶数的选择

对于结构复杂、电尺寸较小的问题（如连接器和芯片上的电感等），特别是选择了对于良导体内部进行场求解的情况（即 Solve Inside ），推荐选择 0 阶基函数求解，并将 Lambda Refinement 的值设置得较小（默认为 0.1 ）。对于电尺寸较大的问题（如抛物面天线等），推荐选择 2 阶基函数求解，并将 Lambda Refinement 的值设置得较大（默认为 0. 6667 ）。对于包含复杂细节、电尺寸又较大的问题，推荐采用混合阶（ Mixed order ）求解。