基于分子动理论的Fluent材料属性设置

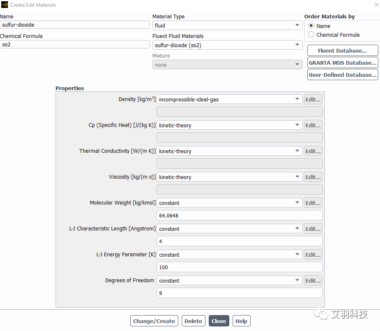
分子动理论方式简介

Fluent的流体材料属性定义中，有一种方式叫做kinetic theory（分子动理论）。纯气体的比热容、热传导率、粘度可设置为分子动理论；气体混合物的组分间质量扩散率可设置为分子动理论。

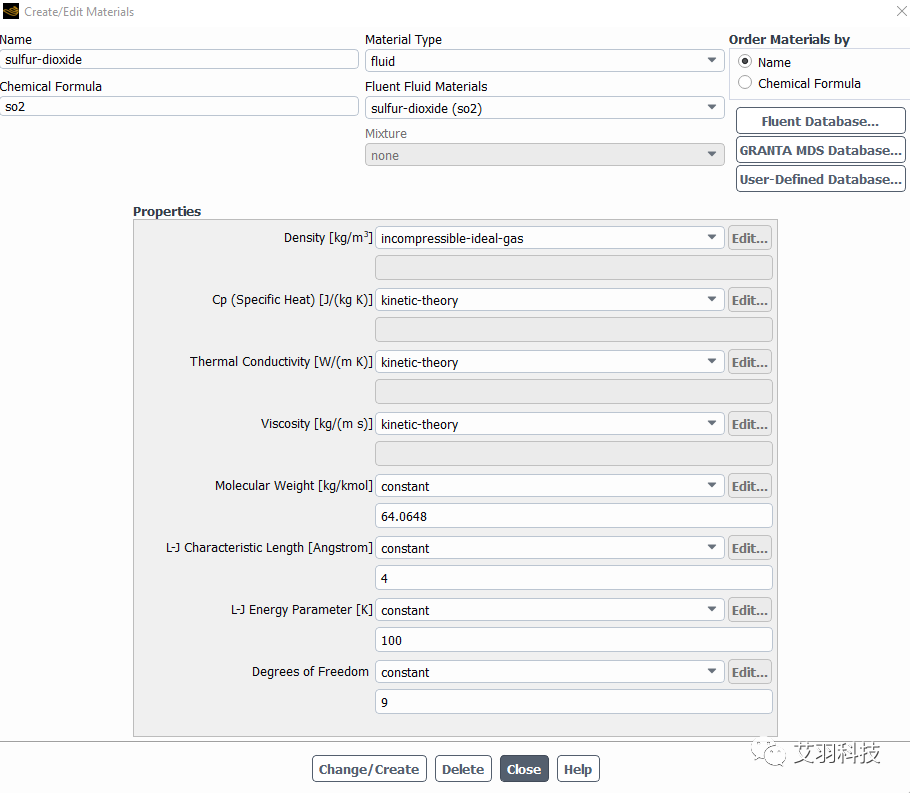
纯气体的设置

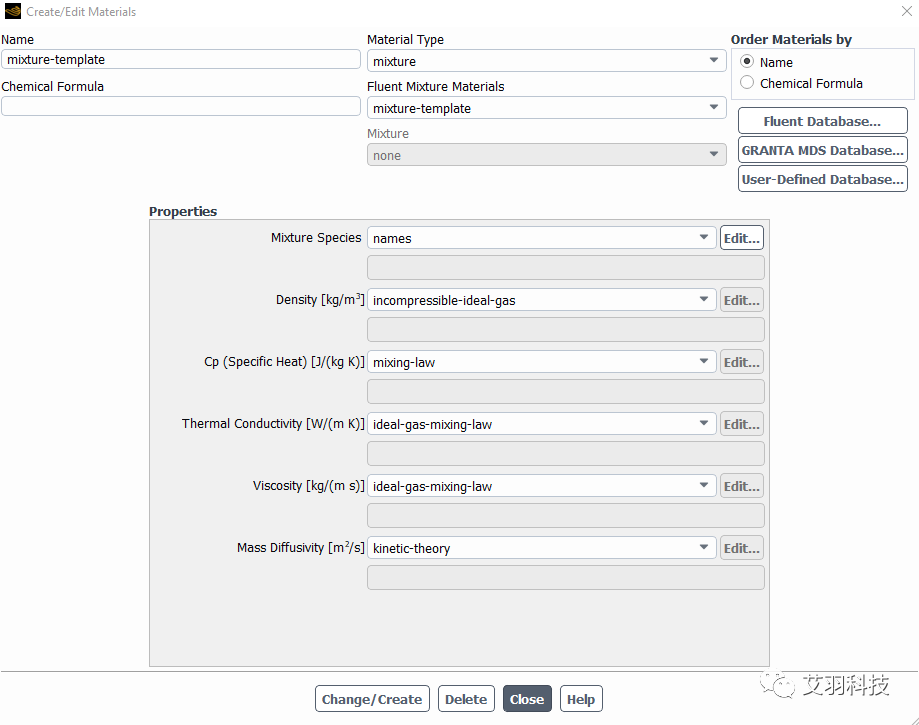
气体混合物的设置

分子动理论方式无需输入各类宏观的材料属性数据，适用于气体介质存在温度变化很大、组分数量极多等属性数值变化较大、难以查找具体属性数值的复杂情况。液体的分子间作用机理远比气体复杂，因此不推荐使用分子动理论方法进行材料属性定义。

一FLUENT

输入信息

采用分子动理论定义材料属性，前提条件为密度采用理想气体方式定义，ideal gas law和incompressible ideal gas law均可，这两种密度定义方式的差异具体可参考Fluent帮助文档。需要输入的数据包括分子量、L-J特征长度、L-J能量参数和分子自由度。这几个参数都是分子微观层面的参数，且为常量，不受温度、压力等外部条件的影响，可查表获取。

1L-J参数

分子间的作用力表现为远距离引力，近距离斥力。L-J势是一种通过势能对分子间作用力描述的理论，由英国科学家John Lennard-Jones提出而得名。L-J势描述的分子间势能和距离关系为：

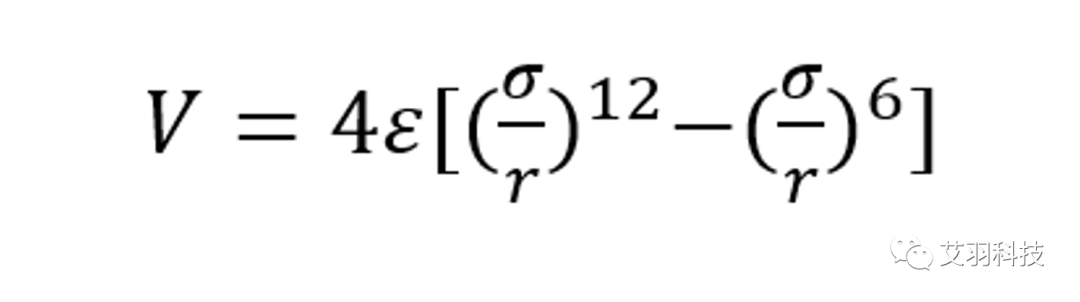
式中，σ 为零势能距离，ε 为势阱深度，均为分子的微观常数。

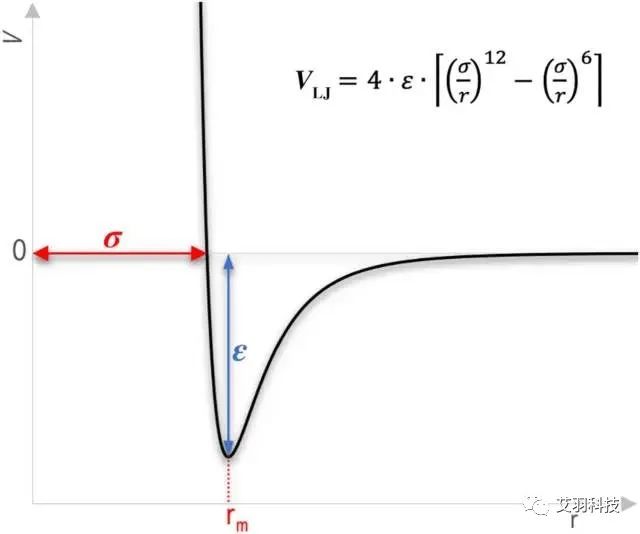
L-J势和距离的函数关系
（图源：《Modified Lennard-Jones potentials for nanoscale atoms》，《Journal of Computational Chemistry》期刊）

在Fluent中，L-J特征长度为 σ（零势能距离）的数值，L-J能量参数为 ε/k（势阱深度/玻尔兹曼常数）的数值，其中 k 为玻尔兹曼常数。需要注意的是，L-J特征长度的单位为angstroms（中文简称埃，简写为瑞典字符 Å，或者特殊情况下简写为英文字母A），其换算为1Å=0.1nm。

2分子自由度

分子自由度是指分子内部原子的运动自由度，包括平动、转动、振动三类自由度。不同分子类型的自由度总结如表格所示，N表示原子数量。

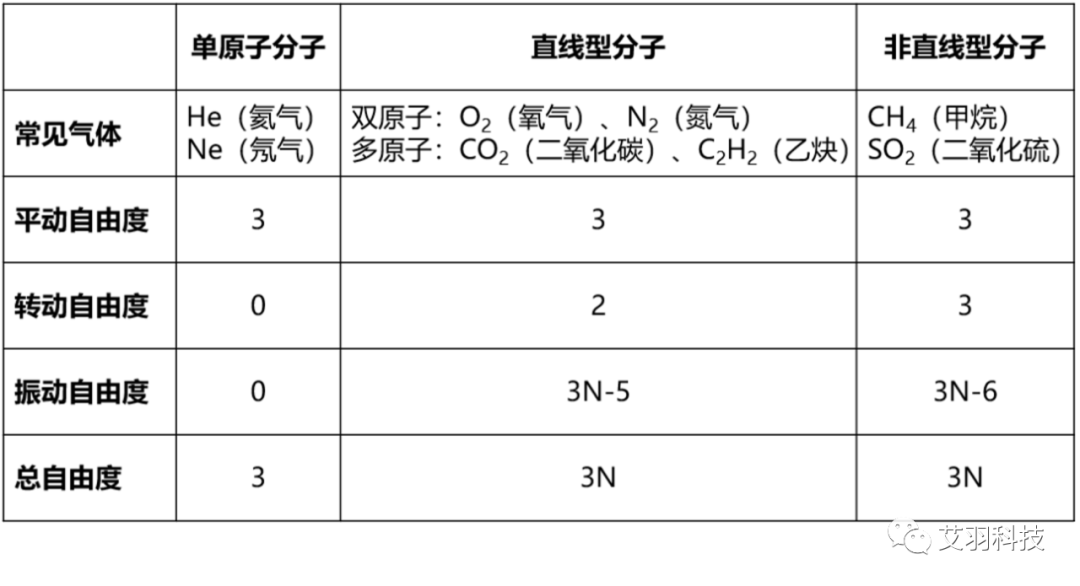
在不太高的温度下，含有振动自由度的分子比例极低，振动自由度可忽略不计，认为仅包含平动和转动两类自由度。温度升高时，含有振动自由度的分子比例不断上升，使自由度数量增加。随着温度进一步上升，多数分子均含有振动自由度，则达到分子自由度的上限3N。

通常的气体完全激发振动自由度的温度（振动特征温度，characteristic vibrational temperatures）极高。常见的双原子气体，仅氯气的振动特征温度低于1000K，为805K，其他常见气体的振动特征温度均远高于1000K，例如氮气为3393K，氧气2274为K，氢气为6332K，一氧化碳为3122K。含有多个振动自由度的气体，每个振动自由度均对应于一个振动特征温度，不同温度下可激发数量不同的振动自由度，情况更加复杂。

振动特征温度的计算公式为

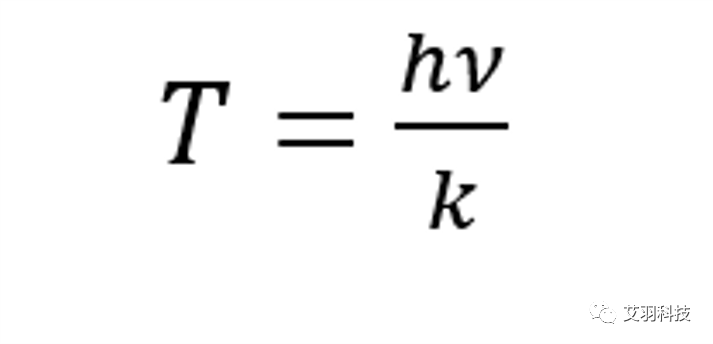
式中，h 为普朗克常数，ν 为分子振动频率，k 为玻尔兹曼常数。

二FLUENT

从微观结构到宏观数据

1比热容

Fluent中比热容为等压比热容。基于理想气体假设，等压比热容和等体积比热容关系为：

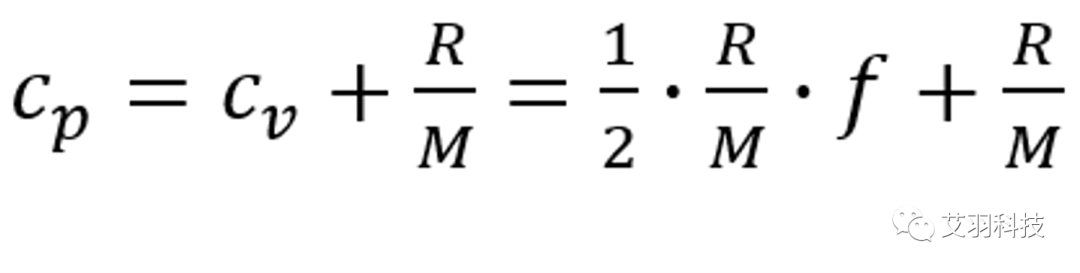
式中，R 为通用气体常数，M 为气体分子量，f 为分子自由度

从公式中可以看出，比热容仅受到分子自由度影响，即受到温度的间接影响。在室温附近的较大范围内，比热容可以认为是常数。

另外，比热容是唯一需要分子自由度数据的材料属性。

2粘度

基于Chapman–Enskog理论，结合L-J势理论，得到以下公式：

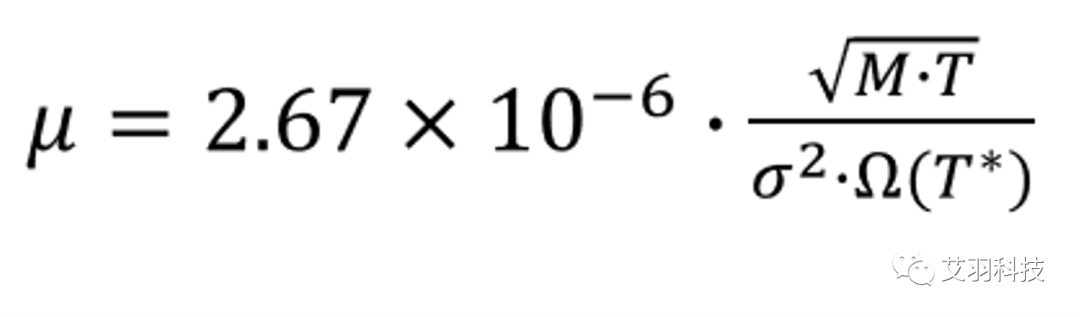
式中， M 为气体分子量，T 为温度，σ 为零势能距离（L-J特征长度，单位埃），Ω 为关于T*的碰撞积分函数（无初等函数表达式）。其中T* 表达式为：

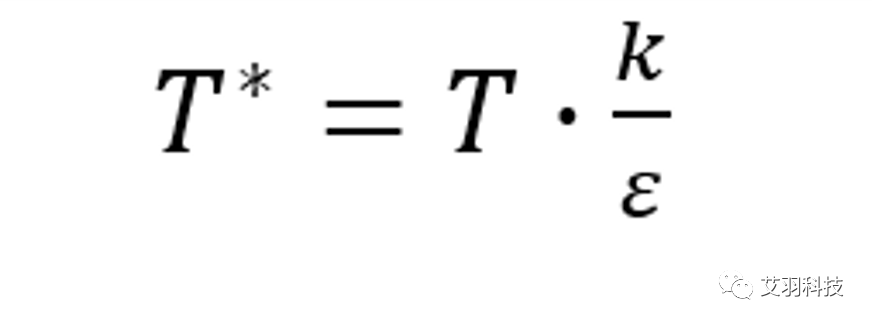
式中，k/ε 为L-J能量参数的倒数。

3热传导率

基于Chapman–Enskog理论，结合Arnold Eucken的工作，热传导率和比热容、粘度关系为：

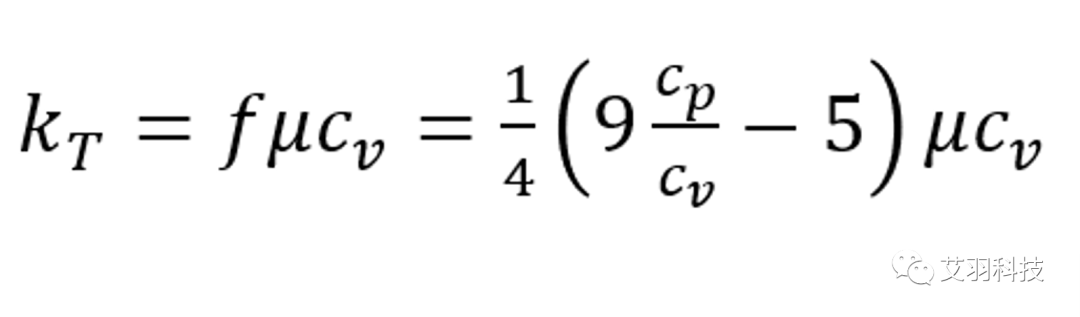
上式结合理想气体的等压比热容和等体积比热容关系，可得：

Fluent计算分子动理论定义的热传导率，其引用的比热容和粘度数据可以采用常数、多项式、UDF等其他方法定义，不需要都采用分子动理论方式。

4质量扩散率

基于Chapman–Enskog理论，混合气体中任意两种组分之间的扩散率为：

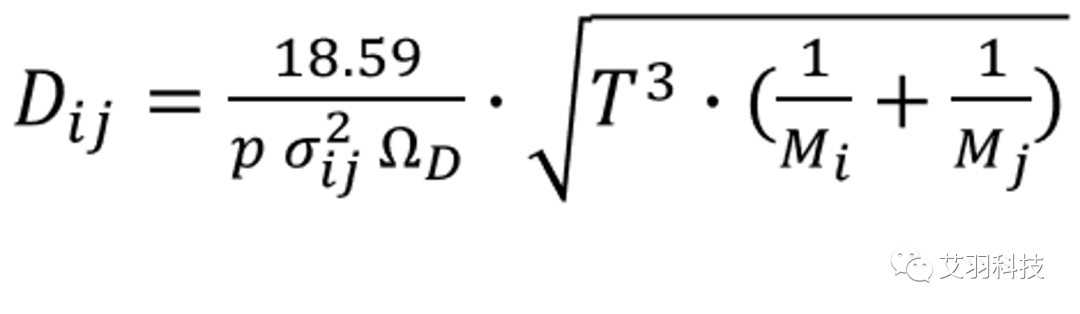
式中，p 为绝对压力， σij 为组分的L-J特征长度的函数，定义为：

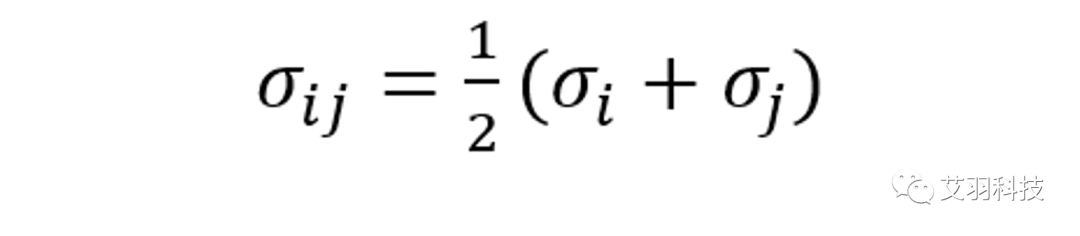
ΩD 为扩散碰撞积分函数，其表达式为：

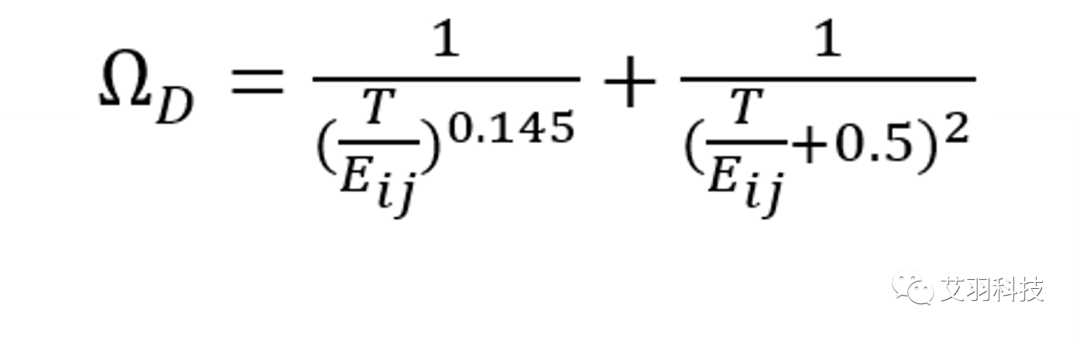
其中，Eij 是组分的L-J能量参数的函数，定义为：

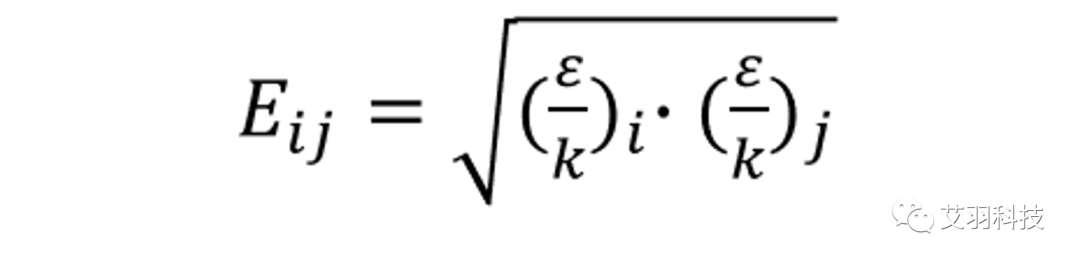
式中，ε/k 为组分的L-J能量参数。

小  结

对于基于分子动理论方式进行定义的材料属性，其均仅为温度的函数，不受压力、密度的影响。具体的材料属性是程序基于分子微观属性进行的函数计算，因此可以减少搜集资料、评估数据准确性等工作的耗时。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删