MATLAB全面使用教程

 1.多项式及其建立

       在运算中我们经常接触到的就是所谓的多项式，比如很常见的一个多项式：

       这里我们就说这是一个x的多项式，最高次是2次，常数项是3，二次项的系数是1，一次项的系数是2，相信这些大家都知道，就不再赘述了。

       那么在matlab中，如何建立一个多项式呢？

        如果在演草纸上，我们需要进行如下的步骤：

        1.确定最高次项是几次。

        2.确定各个次项的系数。

        3.常数项是多少。

       确定了上面的东西，就基本上可以确定一个多项式了，为了方便，我们使用程序表示这样一个多项式： ，那么上述步骤在程序中是这样表示出来的：

clc;clear;%% 使用matlab建立多项式p = [4 3 2 1 1]; %确定各项系数，和常数项。放在一个数组里面。y = poly2sym(p); %创建目标多项式，这个函数返回了一个符号变量，即我们的函数disp(y); %显示y.

        PS: 如果需要定义一个特殊的函数比如  ，那么我们可以认为3次、2次、1次系数都为0，常数项也为0，写入数组即可。

       上面的程序运行结果如图所示：

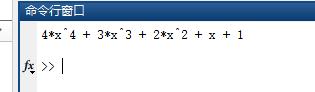
2.通过已知方程的根建立多项式

       假设现在已有方程根： ，要求得到这个方程的式子，对于一元二次方程来讲，一个方法是：伟达定理，利用根与系数的关系，在matlab中，这种问题也可以得到解决，只需要一个函数即可：

clc;clear;%% 使用根建立多项式r = [1 2 3]; %随意编一些根p = poly(r); %调用求多项式的函数y = poly2sym(p); %得到多项式的符号变量disp(y);

       运行结果如图（我还不知道有没有可能求不出来这个对应方程，没试过哈哈哈哈，我猜应该是只要给出一套根，总能给出一个对应方程吧）：

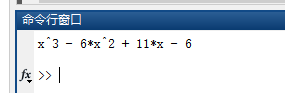
3.对多项式进行求导

       求导即求多项式的导数，一般来讲，习惯上我们把 y = y(x) 对x求导函数直接简称为求导了，但是，我们求导时，一定要明确谁在对谁求导！！！在下文中，不做特殊说明的话，我们默认因变量是y，自变量是x，求导默认为 y对x求导，即求 。

       使用matlab进行求导，代码如下：

clc; clear;%% 对多项式进行求导p = [4 3 2 1 1]; %建立我们的多项式y = poly2sym(p); %得到多项式的符号变量temp_str = sprintf('得到多项式:\ny = %s', y); %将式子格式化到一个字符串中disp(temp_str); %显示p_1 = polyder(p); %求一次导,注意polyder求导传递的是p而不是yy_1 = poly2sym(p_1); %转化为符号变量temp_str = sprintf('求导结果是:\ny_1 = %s\n求导后系数是:[%d %d %d %d]', y_1, p_1);disp(temp_str);

       运行结果如图所示：

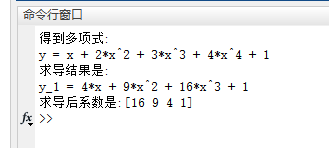
        y_1中的常数1来自于y中的x求导，y中的1求导后成为了0，就没了。

       那么，这仅仅是一个多项式求导，乘积求导、商求导，请继续往下看：

       乘积求导：

%% 乘积求导clc; clear;p_1 = [4 4 2];p_2 = [2 4 5]; % 随意胡诌几个数y_1 = poly2sym(p_1);y_2 = poly2sym(p_2); % 转化为符号变量temp_str = sprintf('原来的两个函数为：\n 1. y_1 = %s\n 2. y_2 = %s', y_1, y_2);disp(temp_str);res_p = polyder(p_1, p_2); % 乘积求导后的系数res_y = poly2sym(res_p); %转化为符号变量temp_str = sprintf('结果为：y = %s', res_y);disp(temp_str);

       运行结果如图所示：

        商求导：

        这个部分比较麻烦，商求导后返回值是有两个，因为很有可能出现求导后还是分数的形式，所以返回值是一个分子、一个分母，代码如下：        

%% 商求导clc; clear;p_1 = [4 4 2];p_2 = [2 4 5]; % 随意胡诌几个数y_1 = poly2sym(p_1);y_2 = poly2sym(p_2); % 转化为符号变量temp_str = sprintf('原来的两个函数为：\n 1. y_1 = %s\n 2. y_2 = %s', y_1, y_2);disp(temp_str);[res_p_Num, res_p_Den] = polyder(p_1, p_2);% 注意此处，与乘积求导几乎一样，只是返回值不同，% 前面的是分子，后面的是分母res_y_Num = poly2sym(res_p_Num);res_y_Den = poly2sym(res_p_Den); %转化为符号变量temp_str = sprintf('结果为：y = (%s)/(%s)', res_y_Num, res_y_Den);disp(temp_str);

       在商求导这个地方，所需要修改的仅仅是返回值而已，其他的地方几乎与乘积求导一致，还是很方便的。

       运行结果如图所示：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删