MATLAB深度使用教程

1.复习定积分（单变量）

       在之前，先复习一下之前学习的内容。使用matlab求解定积分的步骤大概如下：

       1.定义符号变量（syms关键字）

       2.定义内联函数（inline函数）

       3.使用matlab内置函数进行计算定积分或者不定积分（使用int函数，具体求解定积分还是不定积分，根据参数的数量决定）

       我们都知道：定积分是求解一个图形与坐标轴围成的面积。而今天我们需要深入理解一下：定积分是求解两条曲线之间围成的面积，如果只有一个公式，比如x，我们可以理解成 x-0，y=x 这个函数减去了 y=0这个常数函数，或者说，上面函数与x轴围成的面积减去了下面函数与x轴围成的面积（并且这个面积在x轴上方是正的，下方是负的），这样我们就可以推广，假设我们现在有两条曲线，一个是sinx，一个是 ,我们求在0-pi的范围内，两个图形围成的面积，容易知道，两个图形大概是这样围起来的：

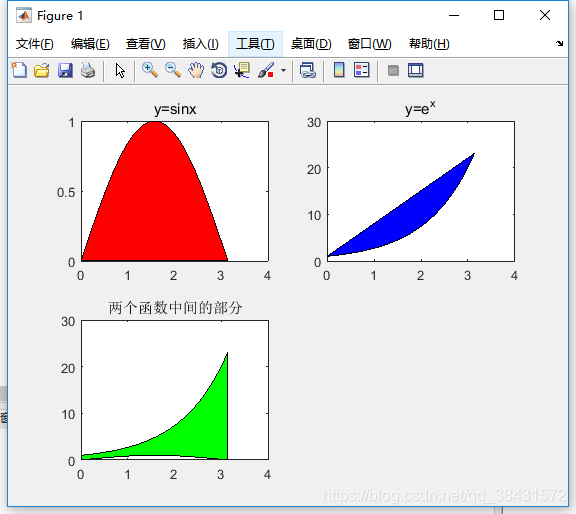
        PS: 上图的代码和讲解如下

%% 目标图像clc;clear all;  % 清除原先的东西 x = 0:0.01:pi;  % x的范围是0-pi，以0.01为一个小分割点细分出一个范围y1 = sin(x);    % sinxy2 = exp(x);    % e^x figure;         % 弄一个figure的框体hold on;        % 保持这个窗体，保证后面的内容都画在了上面，hold off解除 subplot(221);   % 开辟子窗体，221:共2行2列，里面的第一个fill(x,y1,'r'); % 画图并填充颜色，变量是x，函数是y1，颜色是r，红色title('y=sinx');% 设置标题，必需先fill，才能添加标题，否则会失败 subplot(222);   % 开辟子窗体，222，共2行2列，里面第二个fill(x,y2,'b'); % b 蓝色title('y=e^x'); subplot(223);   % 开辟子窗体，223，共2行2列，里面第三个fill([x, fliplr(x)],[y1,fliplr(y2)],'g');                % 两个函数直接填充颜色，每一个方括号代表一个函数的内容title('两个函数中间的部分');hold off;

       OK，那么我们就可以很容易的使用int()函数算出这样一个定积分，代码如下：

%% 对上面的函数进行计算定积分syms x;f = 'exp(x) - sin(x)';res_int = int(f, x, 0, pi);disp(res_int);

       matlab计算结果

2.二重积分

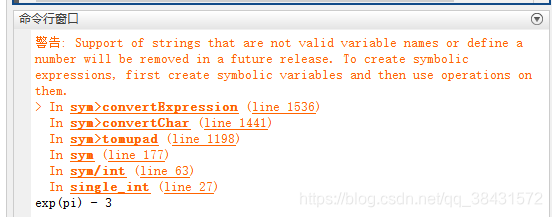
       上面复习了定积分的计算和一般概念，下面我们看二重积分，先了解下二重积分是什么吧：

       二重积分的一个概念是求体积（还有其他的，比如薄片质量等，在这里先不谈，先说体积的问题），那么明确概念其实就不难了，定积分求面积、二重积分求体积，那么这个体积是哪里的体积呢？

       如图，粉红色的是z=f(x,y)的函数图像，下面是地面的阴影部分，红色的是边界，这个体积就是粉色的顶部与底面阴影之间的一个曲顶柱体的体积，那这个体积怎么求呢？

       在定积分中，我们把整个面积分成了无数个小面积，计算后累加，同样的，在二重积分中，我们也采取同样的方法，我们把这个柱体切成一个一个的小柱体，就像图中的那个黄色柱体一样，假设我们把整个底面分成了无数份，每一份的底面积都无限接近于0，假设这个底面积是d ，那么这个地方的高就是f(x,y)，所以这个小柱体的体积就是 f(x,y)d ，我们只需要将这些小体积全部加起来，就能得到整个曲顶柱体的体积公式了：

       并且我们很容易发现，积分的区间其实就是底面，被积函数是曲面的公式。公式中各个符号在下图中体现：

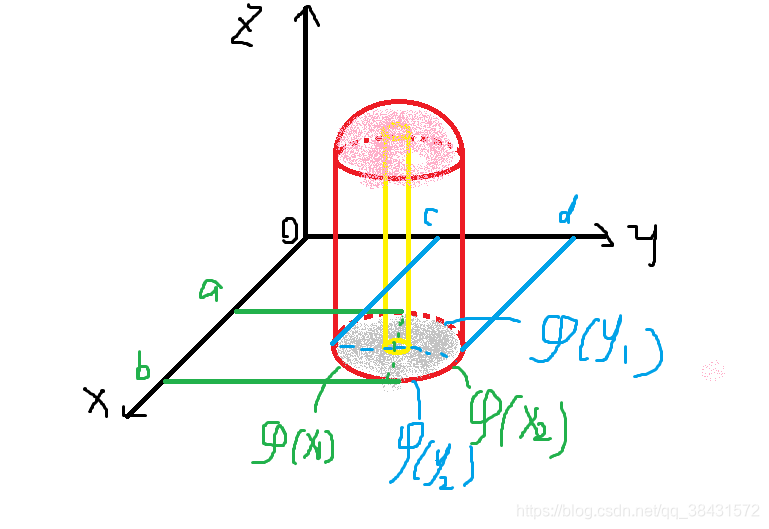
        现在，计算一个例子给大家看，假设底面如图所示（灰色阴影部分）：

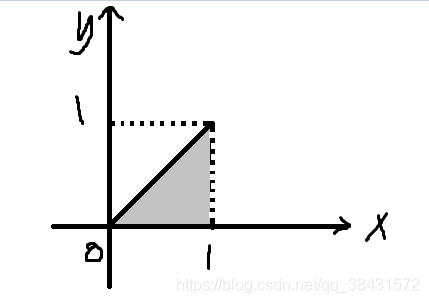
       先积分x(Y型)时区域可表示为：Dx = {(x,y)|0<=y<=1, y<=x<=1}。

       先积分y(X型)时区域可表示为：Dy = {(x,y)|0<=y<=x, 0<=x<=1}。

       下面我们以X型为例，使用matlab计算曲面为 f(x,y) = xcos(y)的曲顶柱体的体积：

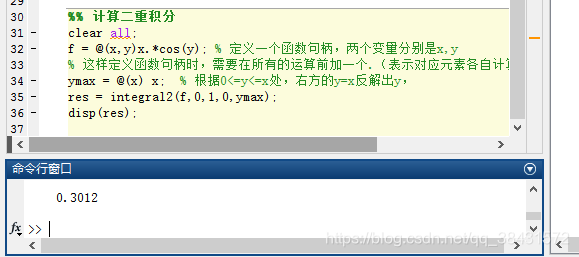
        详细的代码以及注释见下方：

%% 计算二重积分clear all;f = @(x,y)x.*cos(y); % 定义一个函数句柄，两个变量分别是x,y% 这样定义函数句柄时，需要在所有的运算前加一个.（表示对应元素各自计算，不按照矩阵的规则）ymax = @(x) x;  % 根据0<=y<=x处，右方的y=x反解出y，res = integral2(f,0,1,0,ymax);% 计算二重积分的函数 % integral2(fun, xmin, xmax, ymin, ymax)disp(res);

       最后，让我们欣赏一下这个曲面的形状吧：

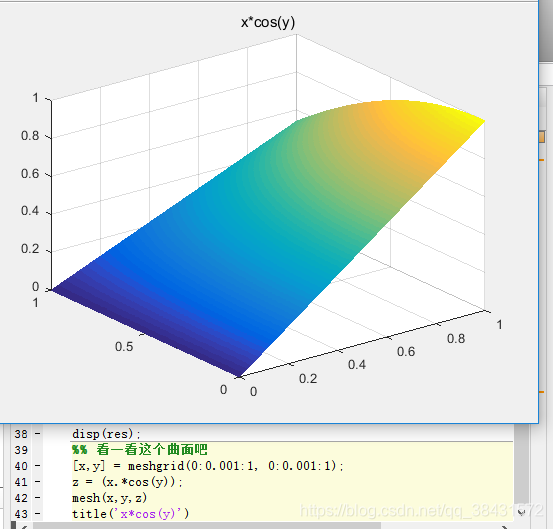
        代码如下：

%% 看一看这个曲面吧[x,y] = meshgrid(0:0.001:1, 0:0.001:1);% 设置x和y的区间，以及细分程度z = (x.*cos(y));  % 使用一个z来代表这个函数mesh(x,y,z)  % 画出二维曲面图像title('x*cos(y)')      

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删