动网格介绍
- 移动/变形网格(Moving/Deforming Mesh,MDM)或动态网格(Dynamic Mesh,DM)
- 可在Fluent内部使用,或在与结构求解器耦合期间使用(FSI = Fluid-Structure-Interaction)
动态网格方法
动网格方法
- Smoothing:所有类型的网格都可以发生变形;
- Layering:添加或去除一层网格单元,只适合结构化网格;
- Remeshing:基于网格尺寸/质量准则添加或去除三角形网格。
重叠网格方法
不采用网格方法
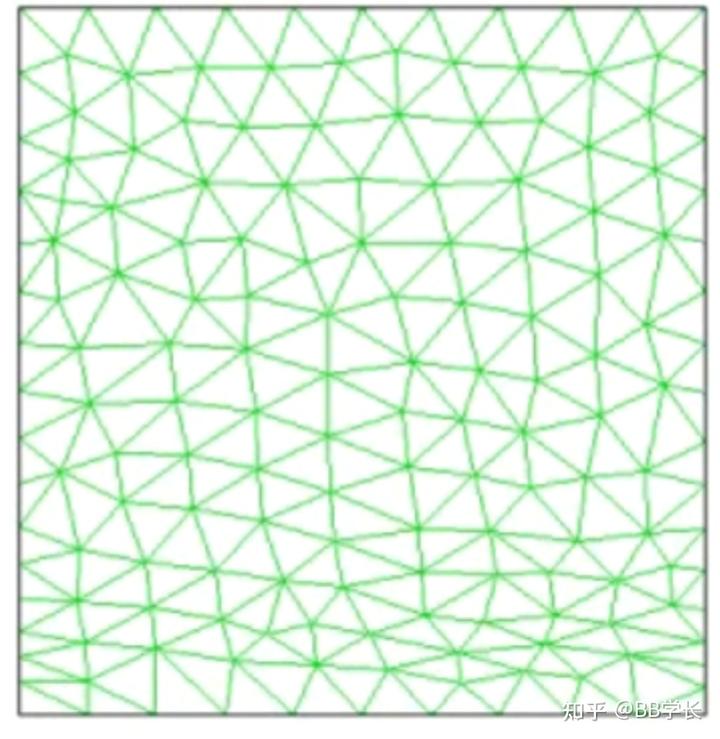
Smoothing方法
- 弹簧近似光滑模型中, 网格的边被理想化为节点间相互 连接的弹簧。移动前的网格间距相当于边界移动前由弹 簧组成的系统处于平衡状态
- 在网格边界节点发生位移后, 会产生与位移成比例的力, 力的大小根据胡克定律计算
- 原则上弹簧光顺模型可以用于任何一种网格体系, 但是 在非四面体网格区域(二维非三角形), 最好在满足下 列条件时使用弹簧光顺方法:
- 移动为单方向
- 移动方向垂直于边界
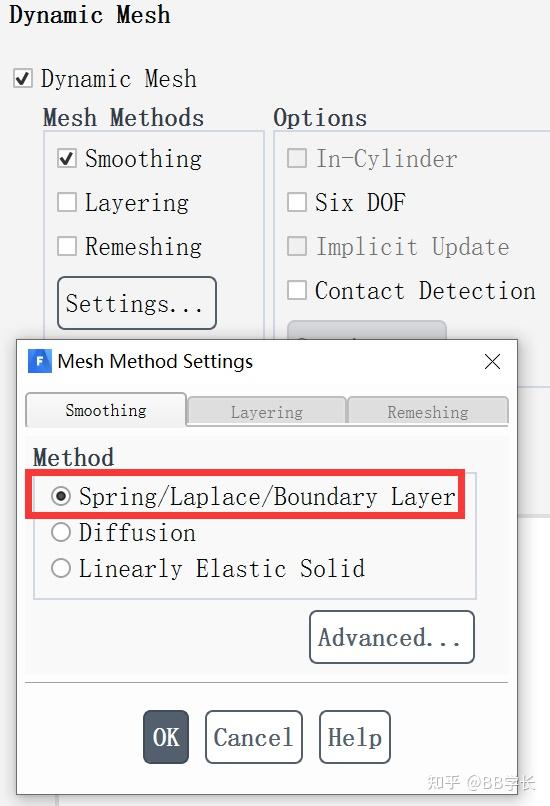
Smoothing方法设置
Spring/Laplace/Boundary Layer
- 任意两个网格节点之间的边被理想化为相互连接的弹簧网络。根据节点上的力平衡,推导出一组线性方程组。迭代求解每个时间步的节点位置。
- Tri/Tet网格默认使用Smoothing方法
- Spring Constant Factor(0-1)控制弹簧刚度。取值为0表示弹簧没有阻尼,边界节点位移对内部节点的运动影响较大。如果值为1时,则弹簧的阻尼是通过计算得到。
- Convergence Tolerance:收敛准则
- Number of Iterations:最大迭代步数
Diffusion
\nabla \cdot(\gamma \nabla \vec{u})=0 \\\nabla \cdot(\gamma \nabla \vec{u})=0 \\
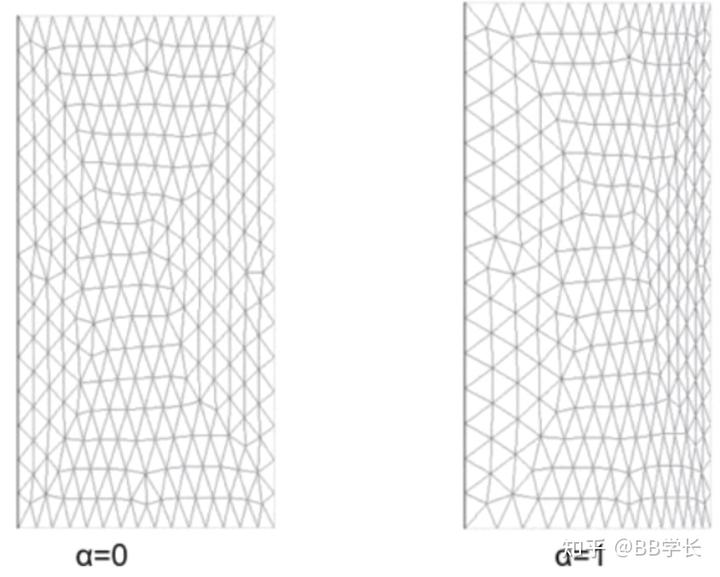
- 扩散系数 \alpha\alpha决定边界运动如何影响内部网格运动:
\left\{\begin{array}{l} \gamma=\frac{1}{d^{\alpha}} \quad \text { boudray distance } \\ \gamma=\frac{1}{V^{\alpha}} \quad \text { cell volume } \end{array}\right.\\\left\{\begin{array}{l} \gamma=\frac{1}{d^{\alpha}} \quad \text { boudray distance } \\ \gamma=\frac{1}{V^{\alpha}} \quad \text { cell volume } \end{array}\right.\\
- \alpha\alpha=0时(默认值),扩散为均布的扩散。 \alpha\alpha越大,大部分网格运动是被挤压在边界网格处。
Layering方法
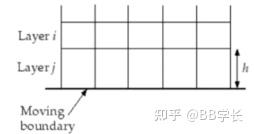
动态层模型(layering)
- 动态层模型的中心思想是根据紧邻运动边界网格层高度的变化, 添加或者减少动态层, 即在边界发生运动时, 如果紧邻边界的网格层高度增大到一定程度, 就 将其划分为两个网格层; 如果网格层高度降低到一定程度, 就将紧邻边界的两个网格层合并为一个层
- 对于棱柱型网格区域(六面体和或者莿形) 或者二维四边形,可以应用动态层模型

Layering方法设置
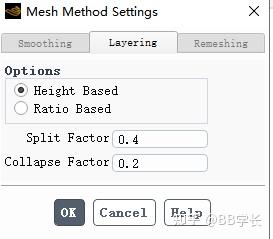
用于统一的边界层高度
- Ratio Based
- 边界层间的高度保持相同的比率
- 当在曲面域中进行分层时很有用
分割边界层: h_{\min }>\left(1+\alpha_{s}\right) h_{\text {tdeal }}h_{\min }>\left(1+\alpha_{s}\right) h_{\text {tdeal }}
合并边界层: h_{\min }<\alpha_{s} h_{\text {ideal }}h_{\min }<\alpha_{s} h_{\text {ideal }}
Remeshing 方法
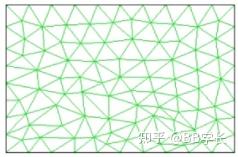
局部重划模型(remeshing)
- 为解决大变形大位移的运动流场问题, FLUENT 在计算过程中将畸变率过大、尺寸变化过于剧烈的网格集 在一起进行局部网格重新划分
- 在重新划分局部网格之前, 首先要将需要重新划分的网格识别出来。FLUENT 中识别需要重构网格的判据:
- 用于四面体网格和三角形网格
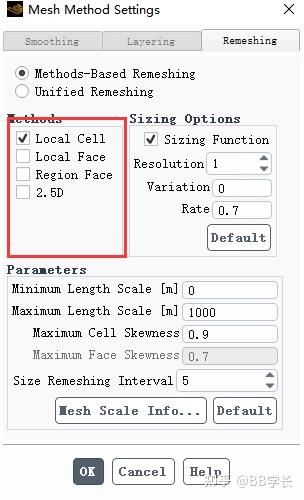
Remeshing 方法设置
- 局部网格重划方法(Local Cell)只会影响三角形和四面体网格;
- 局部面网格重划方法(Local Face)仅在3D中可用,可以重网格边界层中的四面体单元和楔形单元。
- 区域重划网格方法(Region Face)将所有网格类型替换为三角形四面体网格(分别在二维和三维域中),可以在三维边界层网格中重划网格并产生楔形/棱镜网格。
- 二维三角形网格和三维四面体网格采用面域重网格方法(Region Face)。在三维领域中,面域重划网格方法同样可以在三维边界层网格中重网格并生成楔形/棱柱单元。
- 2.5D重网格方法只适用于六边形网格或从三角形表面元素挤出的楔形/棱镜网格。
尺寸函数
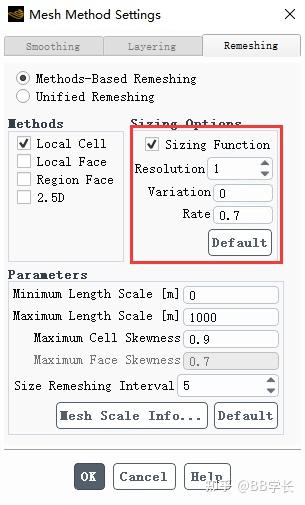
- Variation( \alpha\alpha)控制内部网格相对于其最近边界网格的大小。变化范围从1到无穷。 \alpha\alpha=0.5时表示内部网格大小最多可以是最近边界网格大小的1.5;相反, \mathrm{a}=-0.5\mathrm{a}=-0.5表示边界内部的单元格大小可以是最近边界单元格大小的一半。; \alpha=0\alpha=0,表示距离边界的大小分布不变。
- Rate( \beta(-0.99<\beta<0.99)\beta(-0.99<\beta<0.99))控制网格大小随边界变化的速度。 \beta>0\beta>0,表示从边界到指定的大小函数变化值的较慢的过渡。相反, \beta<0\beta<0表示从边界到大小函数变化值的更快过渡。 \beta=0\beta=0,表示网格大小在远离边界处呈线性变化。
- Resolution决定了用于评估与当前网格的最短特征长度相关的大小分布的背景箱的大小。默认情况下,大小函数分辨率在2D问题中为3,在3D问题中为1。
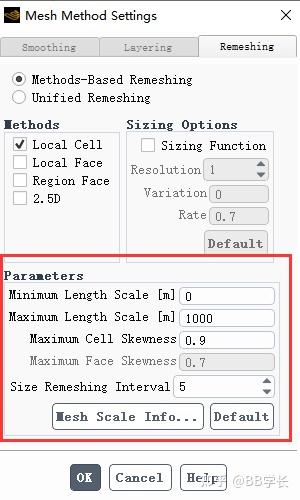
参数
如果网格满足以下一个或多个条件,ANSYS FLUENT会对每个网格进行评估并标记其进行重划网格:
- 偏斜度(skewness)大于指定的最大偏斜度。
- 小于指定的最小长度刻度(minimum length scale)。
- 大于指定的最大长度刻度(minimum length scale)。
- 高度不满足指定的长度比例(在移动面区域,例如,在移动活塞的上方)。
Unified Remeshing
(该方法是在2021版本以后才有)
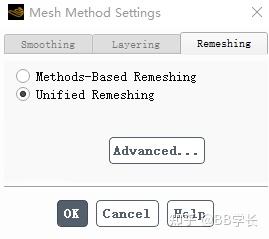
- 进一步简化动态网格设置与统一网格
- 简单的复选框,使它充分为大多数情况下
- 将很少需要调整的偏度限制移动到高级设置
— 默认采用“Retain Size Distribution”方式
- 初始网格用于控制重新划分时的网格大小
- 当对象移动时,基于初始网格控制移动尺寸函数

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删














