零点的电路形式如下,它就是一个低通滤波器;

低频滤波电路
单零点的补偿电路实现方式以及Bode图如下:
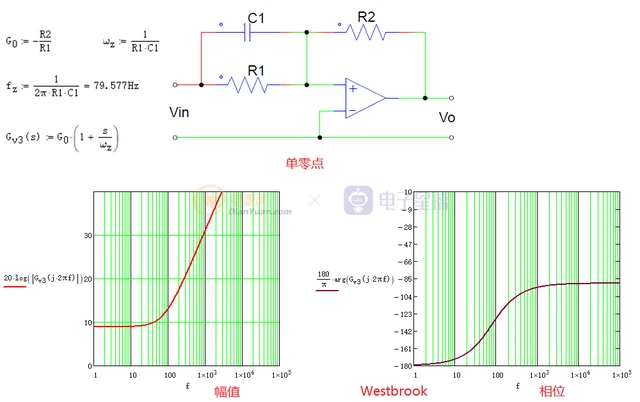
单零点电路以及Bode图
为了实现开关电源的宽带宽,通常在积分环节之后,总是要加几个左半平面的单零点环节来提升系统环增益的相位,保证系统的稳定性。通常这种左半平面零点在开关电源的补偿电路中是不可缺少的。它的加入能提升开关电源这种系统的相位裕量,但会降低对高频扰动的抑制能力,因此在补偿电路中,还要加上相同数量的左半平面单极点来增强系统对高频扰动的抑制能力。
左半平面的单零点环节除了会在开关电源的补偿电路中出现以外,在开关电源的功率级传递函数中也会出现。例如DCDC功率变换器中因输出滤波电容ESR所等效的左半平面单零点。这个功率级输出滤波电容所引入的单零点位置,从小信号稳定性考虑,宜低一点,也即ESR应大一点;但从开关纹波考虑,则宜高一点,也即ESR应小一点。所以功率级中的输出滤波电容选取应根据稳态和动态要求进行折中。
单极点补偿电路实现方式以及Bode图如下:

单极点电路及Bode图
其实我们可以把它看成一个等效的一阶低通滤波器,该一阶低通滤波器的转折频率即为其极点频率。
为了实现开关电源的宽带宽,通常在积分环节之后,先要加几个左半平面单零点环节来提升系统环增益的相位,然后再加个左半平面单极点来提高系统康高频扰动的能力。所以这种左半平面单极点在开关电源的补偿电路中是不可缺少的。它的加入能大大提高开关电源这种系统的抗干扰能力。但左半平面的单极点环节并不是越多越好,在采用光耦隔离的开关电源中,由于光耦的延迟效应,在光耦电路中往往也会引入一个等效的左半平面极点,这个极点的位置与所用的光耦有关,正是由于光耦的这种特性,使得采用光耦隔离的开关电源,所能实现的带宽比非隔离开关电源所能实现的带宽要低很多。
双极点的电路形式如下:

双极点LC电路
双极点环节一般只出现在开关电源的功率级小信号传递函数中,从物理意义上,可以把它理解为一个二阶低通滤波环节,由于功率变换器要实现输出电压的低开关纹波,所以这个环节的双极点频率要低很多,它由功率变换器的开关频率、输出滤波电感、输出滤波电容及其ESR决定。正式因为多数功率变换器在CCM下都有这个双极点环节,所以在用电压型控制的开关电源中,为了能实现稳态的无静态误差,必须在补偿方案中先用一个积分环节(引入零频率极点,提高低频增益),加上积分环节后,系统环增益的最大相位就可能滞后-270度,为了实现足够的带宽,就要再在补偿器的合适频段中,加上两个左半平面的单零点,来提升开环增益的相位,单所加的零点会带来电源抗干扰能力的降低,因此还得在零点之后再加一个左半平面的单极点来保证开环增益对高频扰动所需要的抑制能力。
由此可以看出,对于一个具有二阶双极点的功率变换器,在采用电压型控制模式时,它的补偿器可以选择为具有下列传递函数的结构来实现。

单零点双极点补偿电路实现以及Bode图如下:
单零点双极点电路及Bode图
单零点双极点一般适用于功率部分只有一个极点补偿。如:所有电流型控制和非连续方式电压型控制。零点越低,相位提升越明显,但低频增益也越低;极点的选取一般时用来抵消ESR零点或RHZ零点引起的增益升高,保证增益裕度。
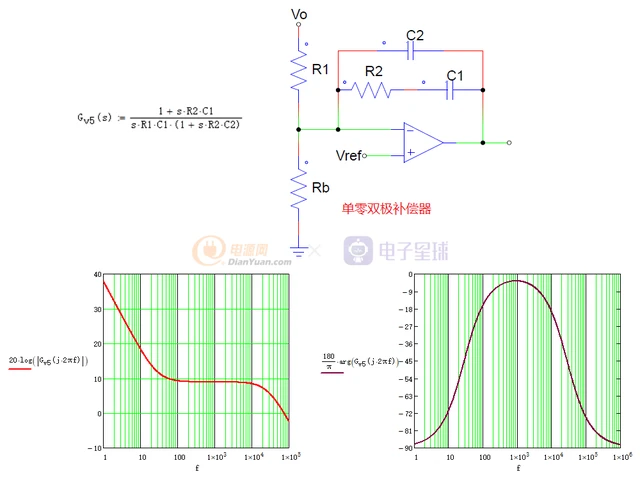
双零点三极点补偿电路实现以及Bode图:

双零点三极点电路及Bode图
适用于输出带LC谐振的拓扑,如所有没有用电流型控制的电感电流连续方式拓扑。由于输出有LC谐振,在谐振点相位变化很剧烈,会很快接近180度,所有需要3型补偿放大器来提升相位。
在原点有一极点来提升低频增益,在双极点处放置两个零点,这样在谐振点的相位为-90+(-90)+45+45=-90,在输出电容的ESR处放一极点,来抵消ESR的影响,在RHZ处放一极点来抵消RHZ引起的高频增益上升
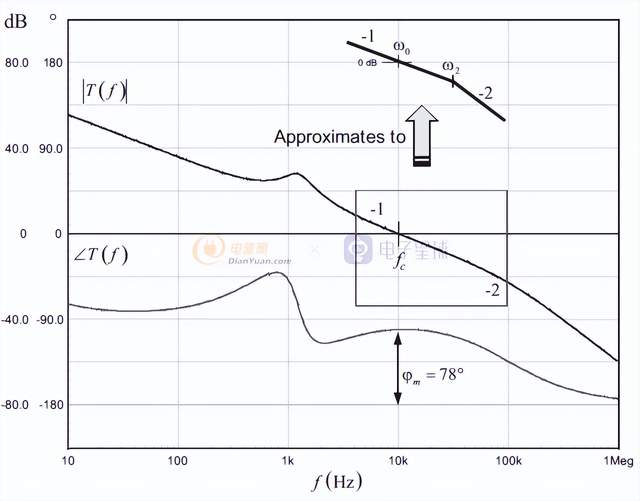
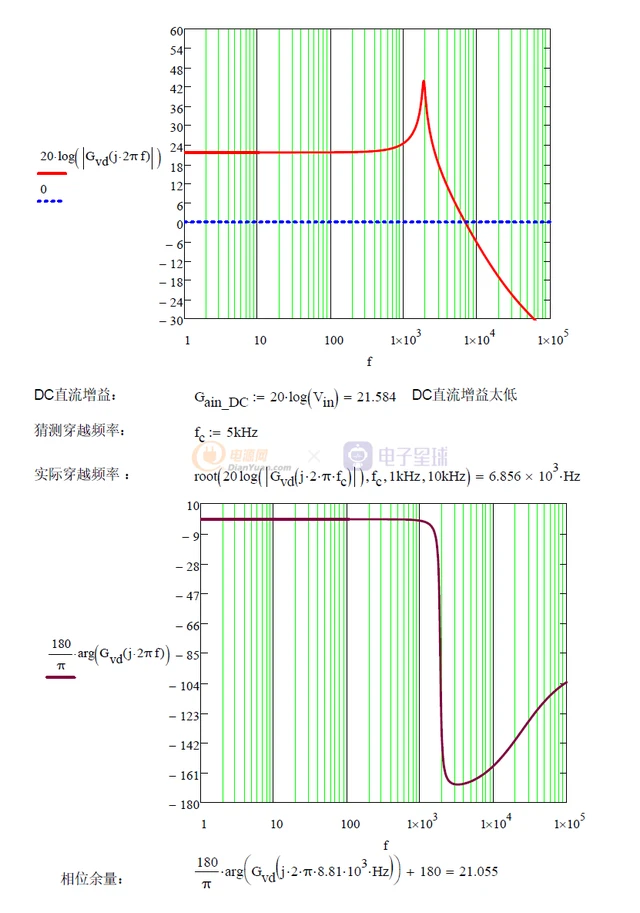
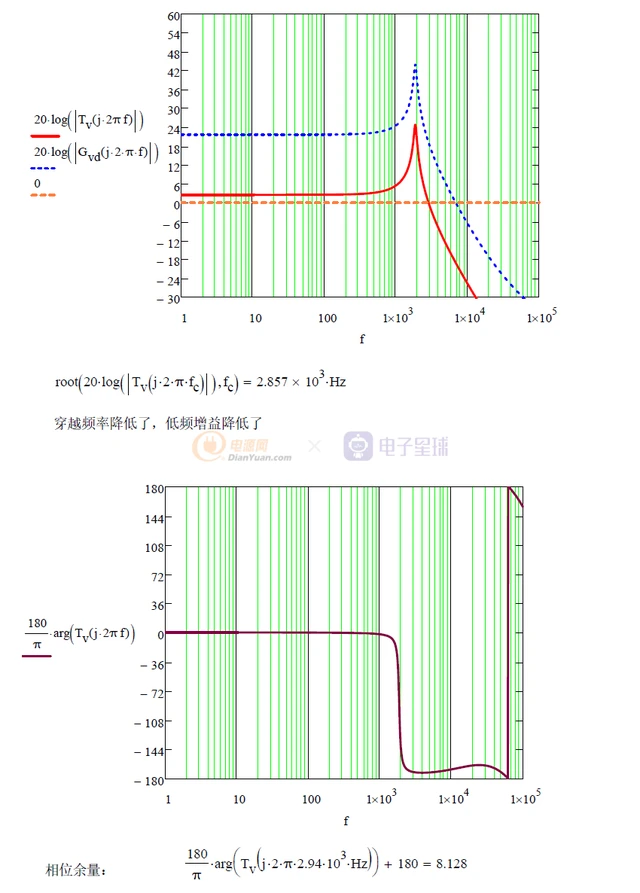
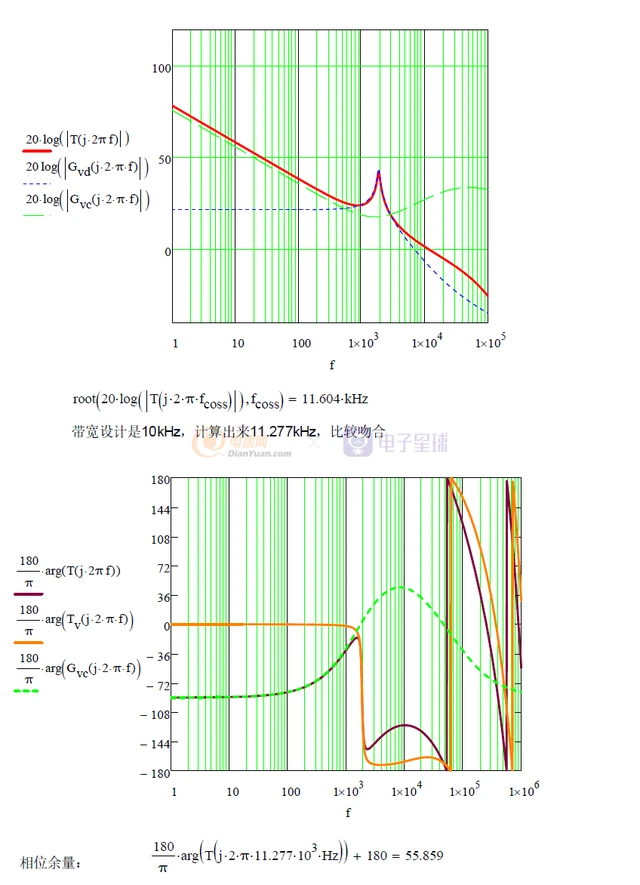
针对Buck变换器所等效的二阶LC低通滤波器的传函,我们采用Type 3型补偿器来进行补偿。具体补偿的原则是:系统需要在低频段存在一定的开环增益,才能对这些频率段的扰动产生抑制作用。但为了保证系统的稳定性,还需要限制带宽,使得频率增加时减小开环增益。此外,为了获得足够的相位裕度,需要减小穿越频率处的相位滞后,通常设计环路增益在穿越频率处具有-1的斜率,也就是系统在穿越频率fc前后具有单极点响应特性。
但同时,当相位滞后达到180度时,环路增益必须足够低以保证良好的增益裕度。因此,为了加快系统在穿越频率fc后的增益衰减以确保足够的增益裕度,通常在穿越频率点后设置系统的第二极点。一般在理论上为了不影响穿越频率,将第二个极点放在10倍穿越频率处,为什么?因为相移在1/10极点频率处就开始。由于增益是以-1的斜率穿越0dB,所以产生的最大相移为-90°,这样系统的相位余量偏大,需要将相移减小,工程上满足45°即可。所以需要将第二极点的频率提前,可以将第二极点放在穿越频率处,这样会在该频率处产生45°相移,还有90-45=45°的余量,但是穿越频率会受到影响(减小),所以该极点需要进行合理设计。
这样,可以看到双极点的配置,它包括一个0dB的穿越极点w0和一个高频极点w2,可以近似表达为:

穿越频率附近可以近似为二阶系统的带补偿变换器的典型开环响应如下:
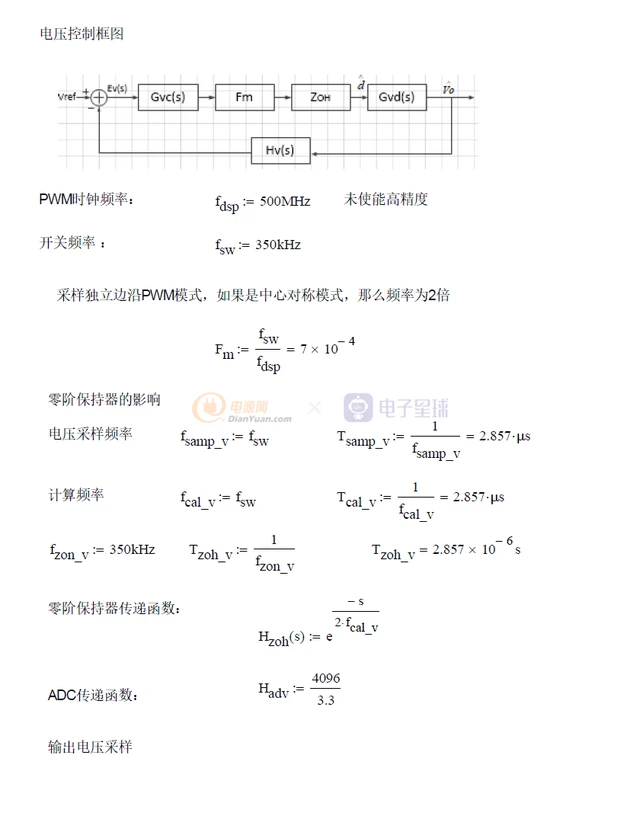
我们先来看整个电压控制的电路图:
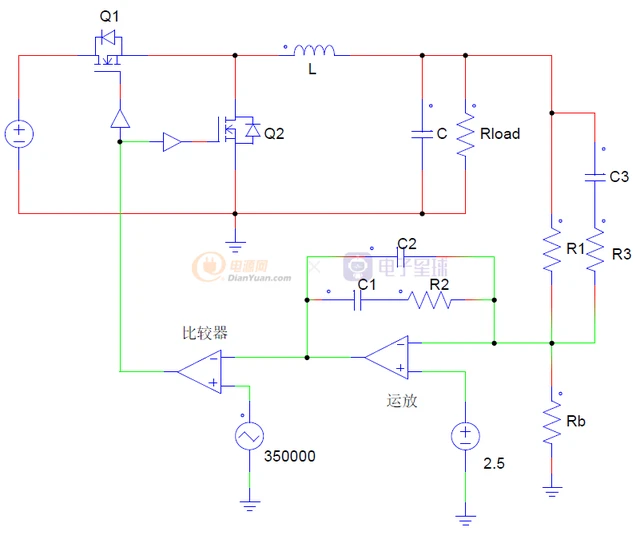
VMC控制框图
Buck电压环等效控制框图为:

控制框图
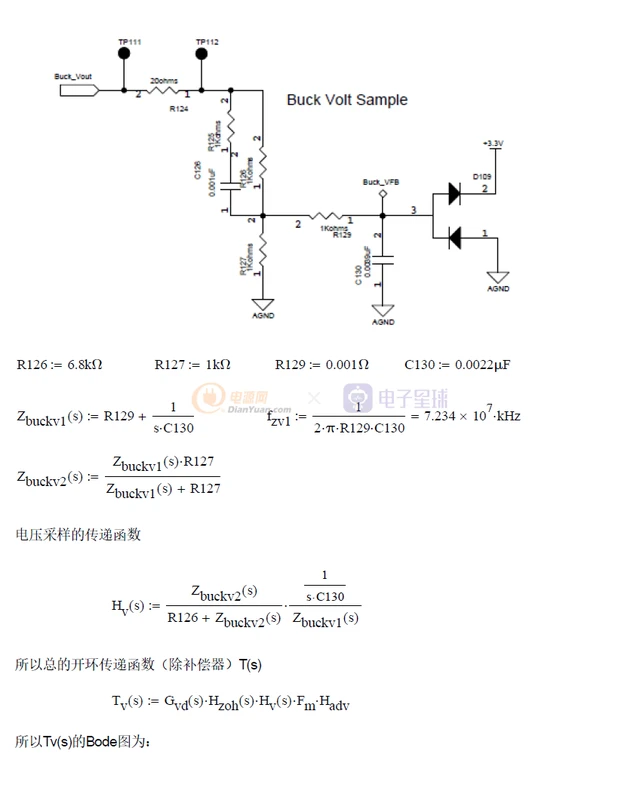
现在我们已经知道控制d到输出Vo的传递函数了,那么同时就要把Hv(s),Fm和ZOH的传递函数找出来,开环传递函数T(s)= Hv(s)*Gvc(s)*Fm*ZOH.后面我将通过DCDT来进行设计。
另外需要说明的是,在进行S域补偿设计时,一定要考虑延时的影响。延时主要由硬件延时、采样延时、软件计算延时等组成,虽然延时对开环特性的增益不会产生影响,但是对相位有比较大的影响。





原文链接:https://www.dianyuan.com/eestar/article-562.html
数字控制相对模拟控制的优点主要是易于采用先进的控制方法和智能控制策略,提高 电源模块的性能;控制灵活,系统升级方便,甚至可以在线修改控制算法(比如Micrcochip dspic33c独有的Live Updata功能,可以不掉电升级),而不必更改硬件电路。系统可靠性高,易于标准化,维护方便;系统的一致性较好,体积小,成本低,生产制造方便。
模拟的控制系统:

Type 3补偿器模拟控制框图
数字控制系统:

全数字控制框图
模拟和数字控制环的主要区别之一是,前者所有的值在时间和幅值上都是连续的,而后者的值在时间和幅值都是离散的,时间是离散的是因为信号采样以固定的周期重复进行。幅值是离散的是因为ADC将输入值映射为一组有限的输出可能值。
但是数字化PWM开关电源都固有地存在一个开关周期的失控时间,例如当系统在某一个开关周期内发生变化时,这个开关周期的脉冲宽度已经确定,因而只能在下一个开关周期进行调整,不过dspic33c有立即更新的功能,即立即在当前周期进行改变,尽量减少环路延迟时间。在控制环的数字实现中,必须考虑一些延迟:模数转换的采样/转换时间,环路补偿器计算时间,功率元件响应的某种非零延迟,低通滤波器延迟。可以计算出所有这些延迟的总时间,这个时间就是采样频率的边界条件,因为如果系统在比该时间的倒数更高的频率下工作,采样将没有任何意义。换言之,这是在环内传输系统的任何变化所需要的时间。
ADC 采样-保持ZOH的影响
离散时间的数据序列

DSP内部的ADC模块将连续的信号根据给定的REF和采样时钟等配置,转换为离散的数据序列。
采样过程中ZOH的工作过程示意图如下:
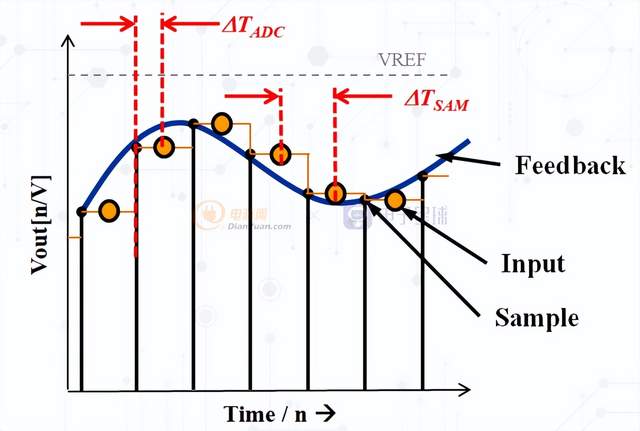
ADC采样示意图
可以看出保持输出的值与实际的值延迟1/2采样周期ΔTadc,而ΔTsam为实际的采样周期间隔。

图中蓝色信号为实际的输入连续信号,红色信号为ADC采样值,绿色信号为采样还原后进入DSP内部的信号(即采样输出信号),采样频率越高,模拟信号的还原度越高,失真度越小。ZOH会引入一个采样周期Ts的延迟,通过ZOH重构信号会比原始信号延迟Ts/2,相位之后w*Ts/2弧度或者180°*(fx/fs)deg。
ADC模块的内部工作示意图如下:

ADC模块工作信号流示意图
采样频率的选择
延迟时间的倒数决定系统可使用的最大采样频率。Nyquist 采样定理证明,为了能够重现初始信号,采样频率必须至少是采样信号最大频率的两倍。值2 实际上仅是理论值;在实际应用中,必须更大些。典型值是6到10。相应地,能够正确操作的最大信号频率是采样频率的六分之一到十分之一。采样值如果选择不当会产生混叠效应。
采样频率是被采样信号频率的9xf
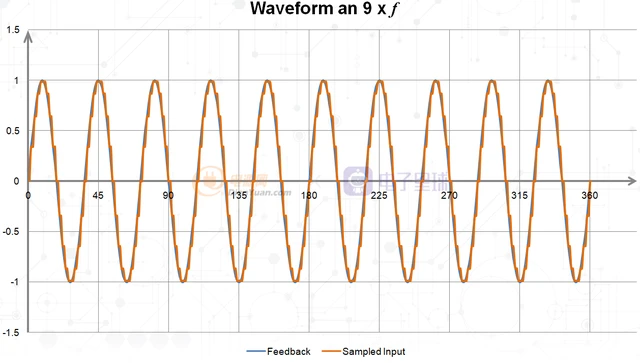
采样频率与被采样信号的频率相等fs=fn

采样频率为被采样信号频率的1/2

最好能使数字环的工作速度尽可能的快,以达到最小环内延迟,从而得到最大可能的采样频率。关键是,如果采样频率高,那么信号最大频率也就高;这意味着控制环可以在系统环境条件下很容易地响应高频变化。
对于数字PWM外设,有两个不同的分辨率:频率的分辨率和占空比的分辨率。频率的分辨率取决于PWM外设所选的时钟源,比如dspic33c默认是500MHz主频,那么PWM分辨率就是2ns,如果使能高精度,那么是8倍默认频率的关系,在高精度模式下分辨率可以做到250ps。占空比分辨率有点类似于PWM分辨率,也就是占空比控制的精细程度。PWM分辨率至少应该比ADC的分辨率高一位;否则,输出值将介于两个ADC值之间,因而系统将不断试图达到稳定状态,从而在这两个值之间振荡。

数字控制的主程序一般由两部分组成:
1、一组初始化程序,其中对所有用到的外设寄存器进行设置(可以采用MCC完成);2、主循环。中断服务程序(ISR)将定期中断主循环,以便低优先级任务能在其他时间在此循环内执行。例如,用于均流、用户接口管理以及与外部单元通信。中断服务程序是数字控制程序真正的核心。
基本操作按如下执行:
1.从ADC硬件收集数据。
2.计算当前读到的系统电压值(VFB)与参考电压值的差。
3.执行PID控制,其输出就是占空比。
4.把计算值固定在最小值和最大值之间。
5.用当前产生的(新)占空比更新占空比。由于中断时间资源的限制,有时无法在每个PWM周期更新占空比。占空比更新频率决定最大控制环的带宽,是响应输入(线性稳定度)或输出(负载稳定度)快速变化的系统功能。例如,如果PWM频率为200kHz,每隔一个周期采样电压/电流并更新占空比,变得到100kHz的更新速率,即系统的两次连续干预的时间间隔为10us
一般数字控制器设计方法采用直接数字法:s域的被控对象首先被转化到z域,控制器设计直接在z域中进行。当然,也有另外一种数字再设计方法,控制器在s域中设计,然后再进行离散化。在数字再设计法中,当采样频率足够高时,由数字控制的采样保持过程导致的时间延迟可以做一个近似表达。在时间延迟环节被线性化以后,就可以根据系统的性能指标在s域中采用Bode图之类的标准设计方法来设计模拟控制器,一旦模拟控制器被设计出来以后,就能够被离散化。
s域到z域的离散化方法建议采用双线性变换,也就是tustin变换:
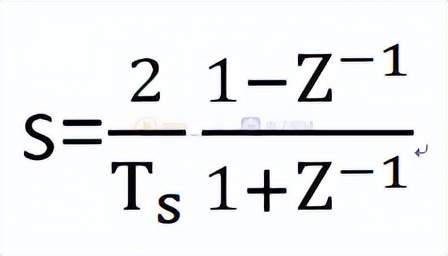
双线性变换法把s域的整个左半平面映射为z平面的单位圆,因而不会影响离散化后系统的稳定性,除此之外,双线性变化发最吸引人的特征是在低于1/10采样频率时同时保留了控制器幅值和相位的频率特性。与被控对象校正后系统开环传递函数的幅值穿越频率相比,当采样频率足够高时,可以采用数字再设计法。
现在以一个s域的补偿器设计为例,流程如下:
1)首先选择一个合适的已知原型滤波器传递函数(要选择合适的零极点);
以3p3z补偿器为例,其常见表达式为:

上述补偿器提供一个零极点,以提高低频增益;提供两个零点wz1和wz2,提供两个极点wp1和wp2.假设提供零点频率800Hz,两个零点 分别为300Hz和900Hz,两个极点分别为500Hz和5KHz,可以如下表达:

2)将改原型滤波器的s域传递函数映射到z域中;
可以利用matlab将上述s域方程进行z域的转换,matlab变换程序如下
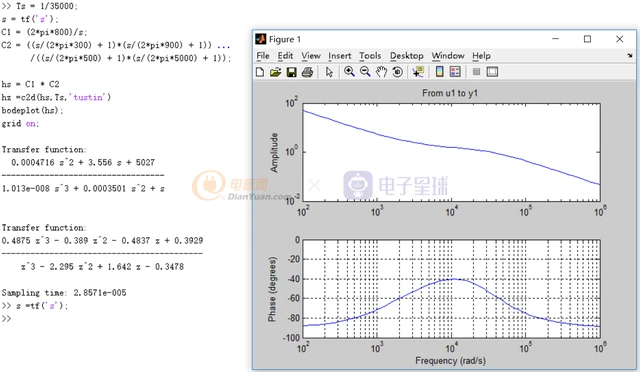
现在得到了z域的表达式为:

e(z)是误差量,u(z)为输出量。
另外举例为一个SZSP的s传递函数如下(极点频率在10Hz,零点频率在250Hz):
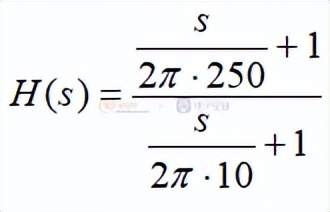
利用matlab变换如下(采样频率100kHz):

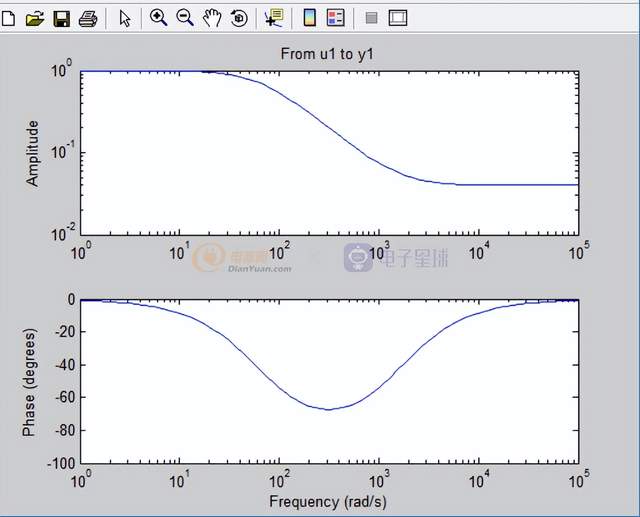
除了matlab可以进行方便快捷的变换之外,数学软件Mathcad也是可以的
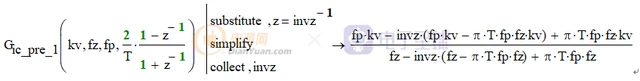
3)将z域转换为时域内的线性差分方程;

由于dspic33系列是16bit定点,所以需要对A/B系数进行Q15定标然后再进行计算
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删