这次准备花费一点时间制作一个全数字电源Demo,基于Mircochip全新dsPIC33C系列。随着数字化的到来,很多传统电源由模拟控制平台转向数字平台,而作为一线工程师觉得数字电源比较难进入,借着这次机会,我将会逐步的介绍全数字电源的详细制作过程。主要内容包括如下:
Demo板的初步规格如下:Vin:9-18Vdc;Vout:3.3-5Vdc;Iomax:2A;工作频率:fs = 350kHz;支持逐周期限流,过流保护,输入输出过欠压保护。
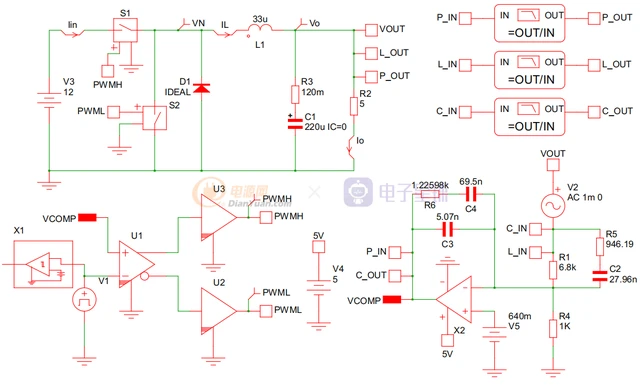
Buck的由来
电力电子的发展史我不想多说,经过几十年的发展由最初的线性电源低效率、大体积到目前的高频、小体积和高效率。下面将介绍三种最基本的拓扑之一Buck变换器是如何演变过来的。
学过电子的应该都知道,如何从一个电压(高)得到自己想要的电压值(低),可能最简单的方式就是通过电阻分压,如下面的方式。
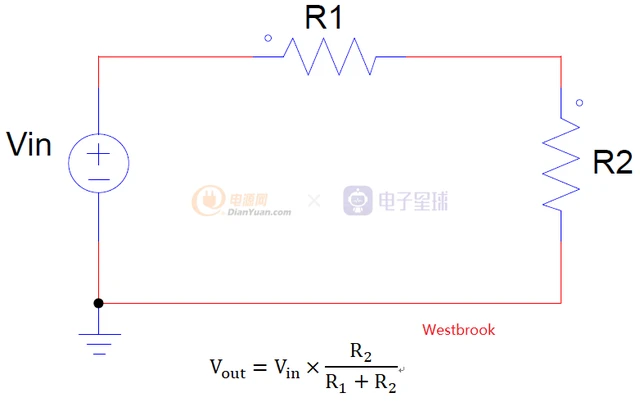
这种方式最方便快捷,现在一般的电压采样基本采用这种方式,但是如果功率稍微大一点呢?由于R1和R2是串联的,所以在R1上的损耗不可忽视,如果所要的电压值远低于输入电压,那么该电路的效率就会极其低下。对该电路尝试进行变形,将R1更换为三极管,也就是现在的LDO模型,如下:
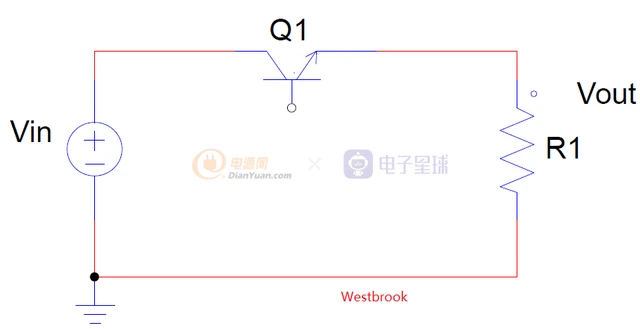
通过变型,那么原来在R1上的损耗转移到三极管Q1上面去了,由于Q1承受输入和输出的压差,所以该电路的效率也比较低下。为了提升效率,之前三极管是工作在线性状态,是否可以更改为开关状态呢?这样三极管就只有开关损耗和导通损耗,那么损耗就会大大的降低。可以更改为如下电路:
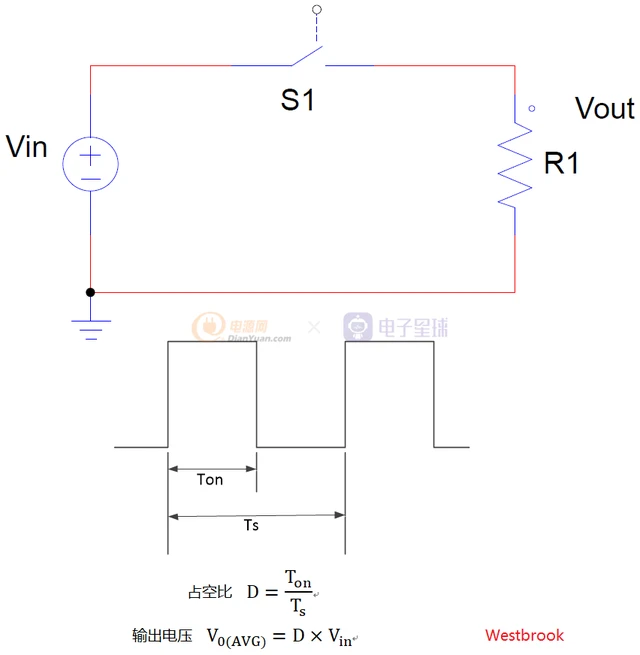
该电路工作周期时间为Ts,导通时间为Ton,那么占空比就是D=Ton/Ts,但是这样输出电压与开关状态高度关联,S1导通时有输出电压,S1关断时没有输出电压,但是输出负载总是需要连续的能量供给,这对于输出端负载是不可接受的。这就需要进行解耦,在变换器一定位置引入储能元器件电容,这样在即使在输入端S1断开的情况下,输出端电容也可以进行持续的能量输出,保证输出电压的稳定。
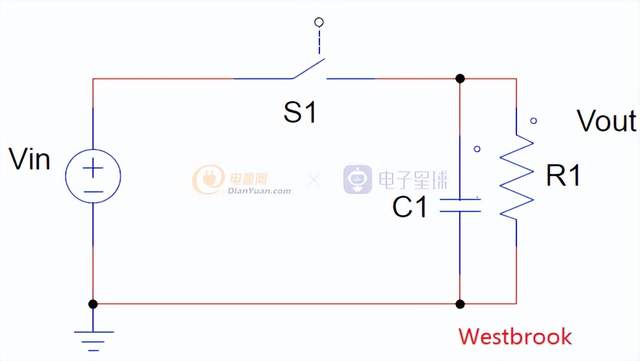
如果这样做,大家有没有看出会带来什么样的效果?由于电容两端的电压不能突变,当S1闭合的时候,那么会在线路中产生一个非常大的冲击电流,它不仅导致噪声和EMI问题,这个时候S1可能会被损坏。所以需要对其进行限流,如下:
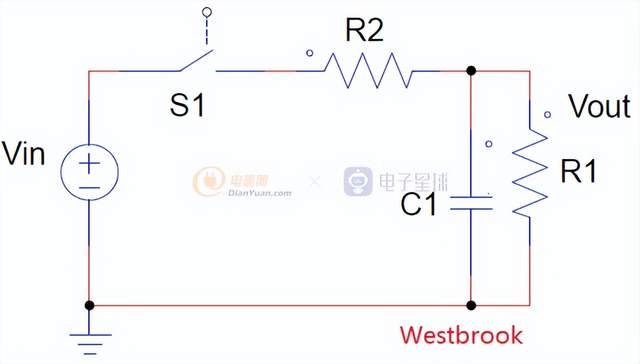
加入R2限流电阻后,在S1闭合瞬间就没有那么大的冲击电流了,但是由于R2是串联在主功率回路中,电阻就会消耗功率,这样,在开关上减小的功耗最终可能又消耗在所加的电阻上。因此,为了最大限度的提高效率,可以将R2变换为电抗元件,从原理上来说,电抗原件仅存储能量不消耗能量,大家知道,电感两端的电流不能突变,所以在开关S1闭合的时候,电感可以很好的抑制冲击电流而不消耗能量。如下:

这样解决了S1闭合时由于C1的作用引起的浪涌冲击电流,但是当S1断开的时候呢?刚才有提到,电感两端的电流不能突变,当S1突然断开,就相当于电感的电流产生了突变,由于没有续流的回路,那么电感存储的能量就会以“拉弧”的方式消耗,这样就会产生一个非常大的电压尖峰。所以,为了给电感L1提供一个续流路径,需要增加一个续流二极管,如下:
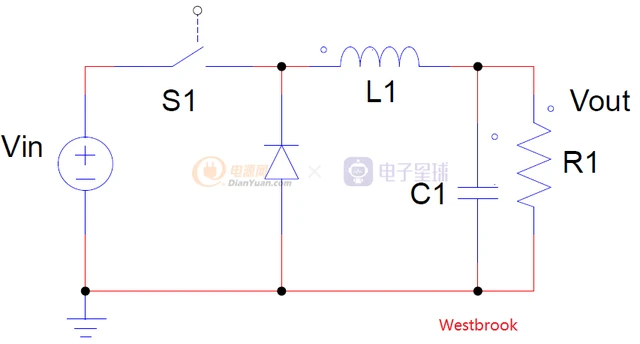
这样,当S1突然断开,L1的能量就会通过二极管进行续流,所以我们也叫续流二极管。当然,为了提升效率,可以将续流二极管更换为MOSFET,如下:

这样一个同步Buck变换器就产生了。可以将电感在不同的位置放置变换为不同的拓扑结构,放在输入端就是Boost变换器,放在下面就是Buck-boost变换器。所以,基本的变换器其实就只有这三种,其他很多拓扑结构都是这三种基本变换器的演变
Buck变换器根据电感电流在一个周期内是否为零,可以分为连续模式和不连续模式:处于稳态工作的Buck变换器,如果电感电流在整个周期内都是连续的,则为连续工作模式(CCM, Continue Current Mode);如果电感电流在周期内某一段时间为零,则为不连续工作模式(DCM,Discontinue Current Mode),处于连续模式和不连续模式之间为临界模式(BCM),此时,电感电流在下一个导通瞬间刚好下降到零。
下面进行CCM模式的Buck变换器稳态分析:

Q1导通
当开关管Q1导通时,电感电路线性上升,给输出电容C1充电的同时也给负载进行供电,电感两端的电压为Vin-Vout:
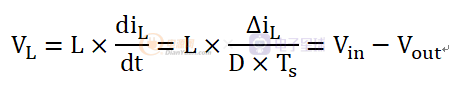
电感电流线性上升:

ΔiL为电感纹波电流,一般在CCM模式下,取电感纹波系数r=0.4:

Q1截止
当开关管Q1截止时,由于电感电流不能突变,续流二极管D1导通,电感续流,电感电流线性下降,此时由C1进行输出负载供电。忽略二极管导通压降有:
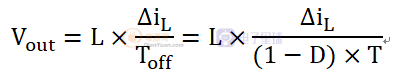
对于稳态工作的Buck变换器而言,导通时电感电流的增加必须与截止时电感电流的减少相等,才能保证电感的磁复位。试想一下,如果不相等,会有什么样的后果?通过一个开关周期内,电感两端的伏秒平衡原理,可以得出输入与输出的关系:
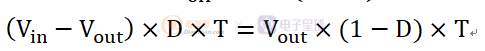
Vout = D*Vin
由于假设电感、电流为理想元件,一个周期内不消耗能量,因此,输出负载电流也就等于电感电流一个周期内的平均值,即Io=IL(avg)。换句话说,Buck变换器电感电流的平均值等于负载电流的平均值,这个结论,不管是CCM,DCM还是BCM都成立。

CCM态
DCM模式下的工作状态:
对于连续模式工作的Buck变换,如果负载电流持续降低,将会出现在一个周期内的某一时段电感电流为零的情况。这种工作模式就是非连续(DCM)的Buck变换工作模式。在每个周期中,DCM的Buck变换有三种工作状态。
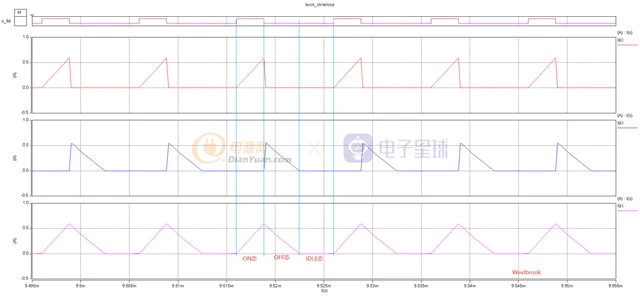
DCM态
ON态:Q1导通,二极管D1截止,电感电流线性增加:
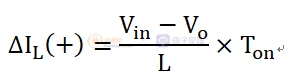
对于DCM模式,上式为电感电流的幅值,也为电感电流的峰值。OFF态:Q1关闭,D1导通,电感电流线性下降:

IDLE态:Q1截止,D1截止,电感电流理论上为零(实际电路中会由于电感电容谐振而存在谐振电流)。所以,在一个周期内,根据电感两端的伏秒平衡关系,得出:

由于是DCM模式,所以Ton+Toff是小于1的。
CCM/DCM边界的确定:
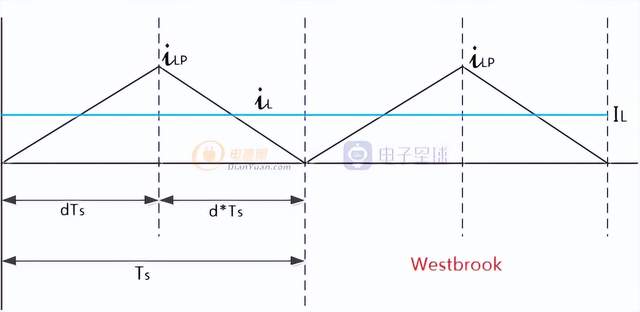
BCM边界
从图中可知:

利用上面边界条件,可以推出Buck变换器的DCM条件:

恒频同步Buck变换器:
一般用肖特基二极管作为续流二极管,但是在低压大电流的时候,由于肖特基二极管也有差不多0.3V左右的导通压降,会对效率影响比较明显,这个时候就提出了同步Buck变换器,将续流二极管更换为Si的MOSFET
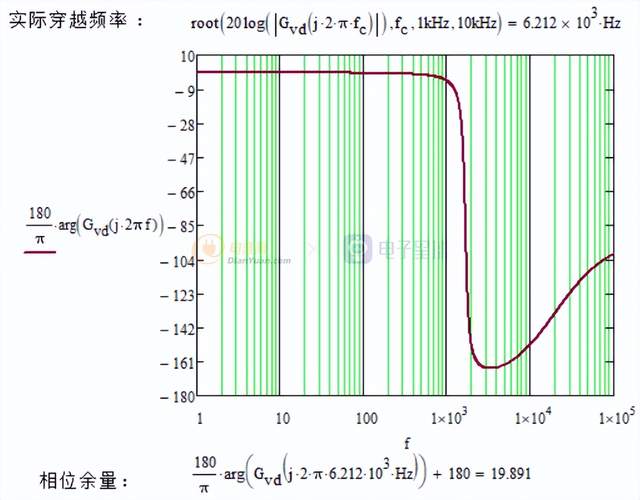
Buck变换器从功率级小信号幅值特性可以看出,是一个典型的二阶低通滤波器,穿越频率为6.199kHz,但是低频DC增益太小,对稳态误差抑制效果不够好。所以需要进行补偿,将低频DC增益提高。

Buck变换器的相位特性如下,可以看到,在穿越频率处相位裕度只有19.891度(如果考虑信号回路的延时,可能就没有裕度了),不满足大于45度的标准,由于幅值在穿越0dB的时候是-2的斜率,所以相位损失比较大,需要对其进行补偿,在幅值穿越0dB的时候使其斜率变为-1。
在所有的拓扑结构中,很容易获得各拓扑结构的输入/输出关系。只要已知了要求的输入和输出电压,剩下的事情就是计算PWM 占空比了。在非常理想的情况下,这就足够了。然而,在实际情况中,事情千变万化。输入电压会变,负载会变(比如说,接通/ 断开输出负载),元件具有容差、使用寿命和温度漂移,当然总是存在噪声。因此,系统性能可能会与所期望的有所不同。在意外情况下,为了使系统行为仍处于控制范围之内,必须加一个“控制环”(硬件和/ 或固件)来控制输出电压。
当任何环境条件变化时,控制环可使设计电路输出电压的变化尽可能小。而且,在某些情况下,控制环可用于防止危险操作情形的发生。电流控制环能够阻止磁通进入变压器。环路的设计与主电路的拓扑和参数有着密切的关系。为了进行稳定性分析,必须建立开关电源完整的小信号数学模型。在频域模型下,波特图提供了一种简单方便的工程分析方法,可用来进行环路增益的计算和稳定性分析。用解析的办法建模只能近似建立其在稳态时的小信号扰动模型,而用该模型来解释大范围的扰动(例如启动过程和负载剧烈变化过程)并不准确,必须配合软启动电路、限流电路、箝位电路和其他辅助电路,才能使开关电源的性能满足要求。
下图是一个常见的控制换,其中G(s)和H(s)是两个模块的传递函数(脉冲响应的拉普拉斯变换)。x(t)表示系统的输入信号;y(t)表示系统输出,它还通过H(s)模块反馈到输入,将H(s)模块的输出r(t)从输入x(t)中减去后,得到误差信号e(t)。

通过计算可以得出输入/输出关系,这个关系被称为闭环增益(Gcl(s))
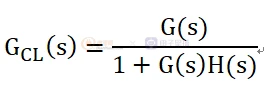
G(s)和H(s)两项的乘积,称之为开环增益T(s)=G(s)H(s)。在控制理论中的关键是仅通过观察开环增益(T(s))的行为就能确定闭环系统是否稳定以及其稳定性如何。在闭环公式中,分母必须不能等于零,否则,Gcl(s)将变为无穷大,系统不稳定。
1+G(s)H(s)≠0,|G(s)H(s)|相位必须≠180°,其中|G(s)H(s)|=1。认为T(s)=G(s)H(s)=1的频率点是fco交越频率。在此频率处的相位必须不等于180°。出于安全考虑,要求相位大约为130°-140°,或者相应的相位裕度=(180°-fco处的相位)≥45°。如图是一个典型的补偿后的环路频率特性曲线,穿越频率是6.5kHz,相位为90度。如果在6.5kHz频率处计算从-180度到相频曲线之间的相位差,那么可以得到90度相位裕度。这是一个鲁棒性非常好的系统,称为“无条件稳定”(当然还有条件稳定,下面解释):即使穿越频率点附近存在适度的环路增益变化,也不太可能移动到相位裕度太小的频率上。

通过一些简化,可得到如下的稳定标准:在fco处,T(s)的斜率必须等于-20dB/十倍频以及在fco处的相位裕度必须至少为45°。这些只是稳定的充分条件,但由于其简洁性,所以得到广泛的应用。
通过观察传递函数T(s),在电源中,传递函数通常用如下形式来处理:
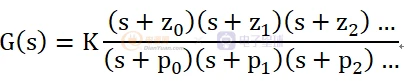
分子的每项都是零点,分母的每项都是极点。在通常情况下,和电源单元中的一样,每个零点是开环增益相位增加+Π/2,而每个极点使其增加-Π/2。从开环增益的角度来看,每个零点引起增益斜率本身+20dB/十倍频的变化,而每个极点引起-20dB/十倍频的变化。因此,在s左半平面的零极点是一个相互抵消的作用
由于Buck变换器是一种典型的低通二阶滤波器,所以就以二阶模型进行分析。典型的二阶LC低通滤波器的原理图为:

RLC二阶电路图
其标准传递函数为:

我们首先来看这个传递函数的根以及对系统动态的影响;
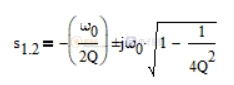
在这个根的表达式中,品质因数Q是关键因素,并分以下三种情况:
(1)Q<0.5:平方根下的表达式为正,系统具有两个独立实数根;
(2)Q=0.5:平方根下的表达式为0,系统具有两个重合的实数根;
(3)Q<0.5:平方根下的表达式为负,系统具有一对带实数部分的共轭复数根;
Q值的变化是如何影响系统响应的?如下是系统在不同Q值条件下的阶跃响应。
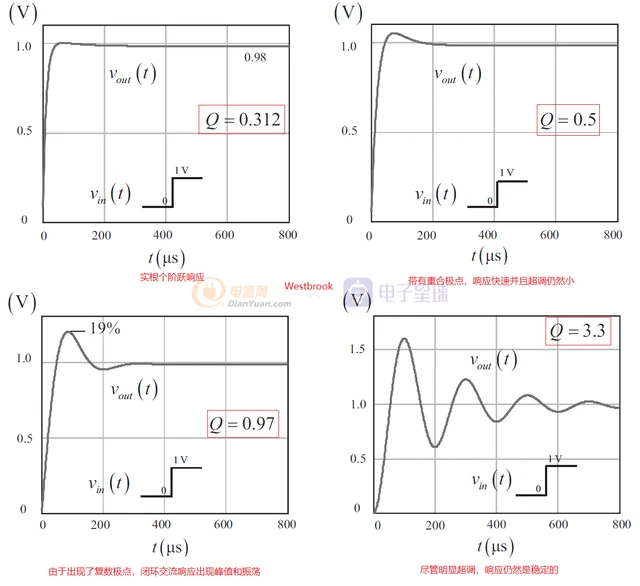
不同Q值条件下的阶跃响应
分析了Q的影响对时域的影响,现在看看根在s平面对系统的响应如何。

所以系统的根只能在S域的左半平面LHP,虽然呈现不同的阻尼,但起码系统还能够稳定;如果根出现在虚轴或者右半平面零点,那么系统不稳定或者不收敛。在系统设计中一定要保证传递函数的根在s域的左半平面。
其中一个最典型的例子就是输出电容ESR的影响,特别是电解电容的ESR受环境温度的变化非常大,由于ESR可以等效为一个零点,ESR的变化就会影响品质因数并改变根的性质,比如一个470uF的输出电容,在25C的典型ESR是90mohm,然后如果考虑温度的变化范围是-40C~+105C和产品生产的离散性,ESR的变化范围是50~200mohm,那么零点的变化范围是1/2x3.14x200mx470u=1.7kHz和1/2x3.14x50mx470u=6.8kHz。我们可以看一下它的根轨迹趋势是如何变化的。
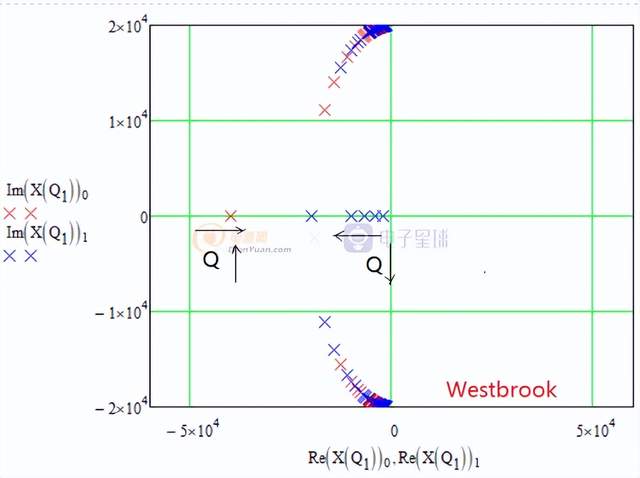
根轨迹图
在整个温度范围内ESR变化导致根的变化,对系统的时域响应也会产生不同的变化,所以有时候工程师在常温测试环路OK,但是在做高低温实验时发现系统不问题,就是这个原因造成的。
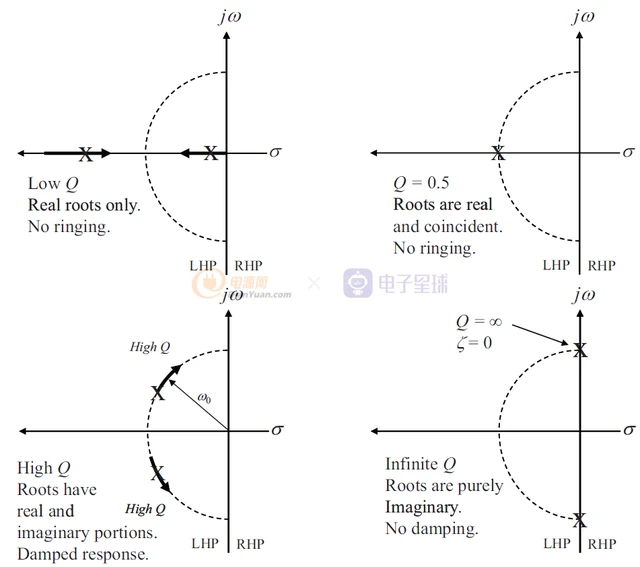
s平面有助于定位根的位置并查看其实部或虚部各自的作用
可以看到,低Q值时两个根是分开的,没有虚数部分;随着Q的增加,沿着X轴相对移动;当Q=0.5时,两个极点重合;随着Q继续增加,极点分离,产生虚部;Q再继续增大,实部(阻尼)趋于消失;当Q->∞,极点最终达到虚轴
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删