1、前处理流程
一般的前处理可按照模型树依次往下执行
(1)General节点:主要设置计算模型总体参数,如选择瞬态或稳态计算、压力基或密度基求解器等。
(2)Models节点:选择计算模型中所涉及的物理模型,并设置模型参数。
(3)Materials节点:选择并设置材料参数。
(4)Phase节点:若涉及多相流模型,则需要在该节点下设置主相和次相,并设置相间作用模型。
(5)Cell Zone Conditions节点:设置计算域属性,包括计算域工作介质、计算域运动状态等。
(6)Boundary Conditions节点:设置计算域边界条件。
(7)Mesh Interface节点:在涉及多计算域问题时,需利用此节点进行计算域连接。
(8)Dynamic Mesh节点:若涉及动网格问题,需要在此节点下进行设置。
(9)Reference Value节点:设置参考值。
(10)Solution Methods节点:选择并设置求解算法。
(11)Solution Controls节点:设置求解控制参数,如设置亚松弛因子等。
(12)Monitor节点:设置定义监视器。
(13)Solution Initialization节点:进行初始化。
(14)Calculation Activities节点:定义求解过程中的行为,如自动保存、动画定义等。
(15)Run Calculation节点:求解设置。
(16)Graphics and Animations节点:设置后处理图形设置,如云图、矢量图等。
(17)Plots节点:后处理曲线定义。
(18)Reports节点:量化后处理结果。
2、网格控制
2.1、网格缩放
导入网格后,如果与实际尺度存在差异,需要对模型进行缩放---scale功能
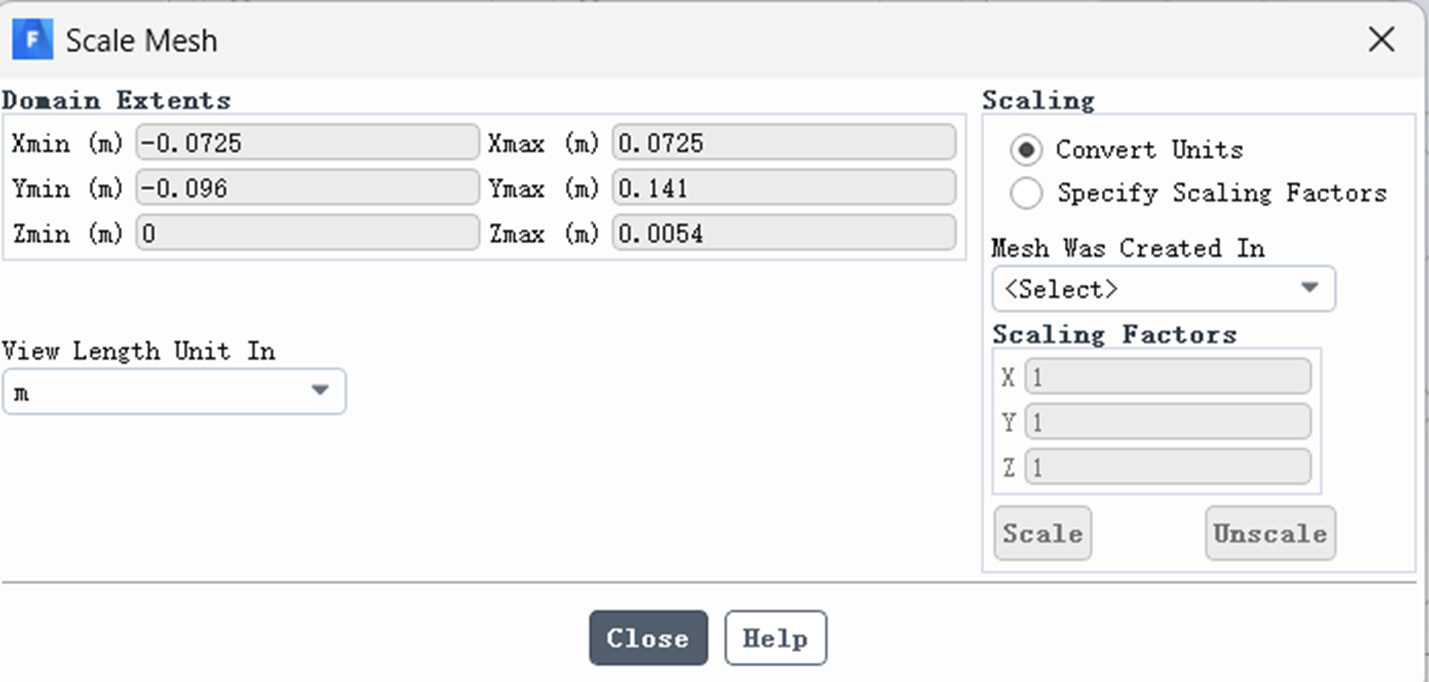
图5.1 网格放缩
Domain extents:计算域尺寸,也就是模型在三个坐标上的尺寸分布,例如上图中的模型x方向上尺寸为-0.0725~0.0725m,
Scaling:放缩方法及缩放的参数
Convert units:采用单位进行放缩,例子:m→cm,缩放因子为100
Specify scaling factors:采用自定的放缩因子
Scaling factors:各向放缩因子
其中mesh was created in 在选择convert units后可选,选定对应的网格创建单位为毫米或者米,在对应的view length units中选择对应需要展示的网格单位
2.2、网格检查(check)
2.3、网格显示
在网格显示中,通常用来显示对应的网格的划分情况。Options下的五项分别为:节点、边、面、分区、重置
如下为选择节点和面所显示的部分

图5.2 选择节点和面所显示的部分
如下为选择节点、面、分区三个所显示的部分

图5.3 选择节点、面、分区三个所显示的部分
Edge type中只有在options中选择edge时才能够进行选择,在surfaces中选择需要展示的面进行展示即可。或者也可以选择new surface进行单个面或块部分网格的展现,具体看个人需求。
Shrink Factor:收缩因子或者收缩系数
3、求解器
3.1、压力基与密度基求解器
压力基求解器分为分离求解器和耦合求解器两种
3.2、密度基求解器
密度基求解器包括显式求解器和隐式求解器
关于两种求解器的说明:
压力基求解器是从原来的分离式求解器发展来的,按顺序一次求解动量方程、压力修正方程、能量方程和组分方程及其他标量方程,如湍流方程等,和之前不同的是,压力基求解器还增加了耦合算法,可以自由在分离求解和耦合求解之间转换,耦合求解就是一次求解前述的动量方程、压力修正方程、能量方程和组分方程,然后再求解其他标量方程,如湍流方程等,收敛速度快,但是需要更多内存和计算量。
区别1:压力基求解器主要用于低速不可压缩流动(Ma<0.2为低速流动)的求解,而密度基方法则主要针对高速可压缩流动而设计,,但是现在两种方法都已经拓展成为可以求解很大流动速度范围的求解方法。两种求解方法的共同点是都使用有限容积的离散方法,但线性化和求解离散方程的方法不同。
区别2:密度基求解器从原来的耦合求解器发展来的,同时求解连续性方程、动量方程、能量方程和组分方程。然后依次再求解标量方程。(注:密度基求解器不求解压力修正方程,因为其压力是由状态方程得出的)。密度基求解器收敛速度快,需要内存和计算量比压力基求解器要大
分离和耦合算法通常是针对压力-速度耦合方程求解的,而显式和隐式则是对时间项的离散而言的
3.3求解方法/算法的选择
选择压力基求解器后,有4中算法:SIMPLE、SIMPLEC 、PISO 、Coupled
其中前三种均为分离算法,后一种为耦合算法,在瞬态问题中一般选择PISO算法
SIMPLE:SIMPLE算法是一种迭代方法,通过将问题分为两部分来解决纳维-斯托克斯方程:一个描述流体运动的动量方程和一个保证质量守恒方程满足的压力校正方程。
SIMPLEC:SIMPLEC(带对流的压力联系方程半隐式方法)是SIMPLE算法的变体,旨在提高原始SIMPLE算法的解的稳定性和降低计算成本。SIMPLEC算法是一种迭代方法,通过将问题分为三部分来解决纳氏-斯托克斯方程:描述流体运动的动量方程、保证质量守恒方程满足的压力校正方程以及考虑流体转移动量的对流方程
PISO :PISO (Pressure Implicit with Splitting of Operators)是一种数值算法,用于解决纳氏-斯托克斯方程。PISO算法是一种迭代方法,通过将问题分成两部分来解决纳氏-斯托克斯方程:一个描述流体运动的动量方程和一个保证质量守恒方程满足的压力校正方程。PISO算法的特点是在求解压力校正方程时使用了一种叫做“操作器分裂”的技术。这种技术可以提高算法的稳定性并降低计算成本。
Coupled:耦合算法是用于解决涉及多个耦合物理系统的问题的数值方法。耦合系统是通过能量、质量或动量交换相互作用的两个或更多物理系统的组合。耦合算法用于在各种设置中模拟耦合系统的行为,包括机械、电气和热系统。耦合算法可分为两类:弱耦合算法和强耦合算法。当耦合系统之间的相互作用相对较弱时使用弱耦合算法,当耦合系统之间的相互作用较强时使用强耦合算法
在这里说一下什么是耦合,在流体动力学中,当两个或更多的流体系统之间相互作用时,这些系统就是耦合的。这种相互作用可能包括能量、质量或动量的交换。举个例子,当一个流体经过另一个流体时,它们之间可能会相互影响导致流体运动的改变。耦合算法是用于模拟这种相互作用的数值方法。
选择密度基求解器后,求解格式有两种,Implicit和Explicit两种,分别对应隐式求解和显示求解算法
3.4稳态与瞬态计算
这里先介绍下稳态与瞬态的概念
稳态:指计算域内的任何一个物理量分布不随时间变化,比如一个圆管里,我假定速度一直是3m/s,过了一天速度还是这么多那么对应的在这段时间内,可以看作稳态处理。
瞬态:与稳态相反,瞬态则表示计算域内的物理量随时间变化的情况
需要说明的是,在自然界中,并不存在标准的稳态或瞬态,只是在特定的模拟场合将其简化,有了稳态和瞬态
另外,在对稳态和瞬态收敛性的判断中,稳态通常根据以下方法判断:
观察残差收敛曲线,是否所有收敛残差均降至所设置的收敛标准,可认为达到收敛
而在瞬态中,每一个时间步相当于计算一个稳态过程,因此要保证每一过程均达到收敛
瞬态时间步长判断:可大致通过以下公式进行预估
分子为局部网格尺寸,分母为特征流动速度
3.5 监视器定义
顾名思义,监视器就是对某一物理量随时间变化情况进行记录
fluent包括三种监视器类型,分别为:残差曲线和力监视器(residuals)、面监视器(surface monitor)、体监视器(volume monitors)
残差和力监视器通常用来监视物理量计算残差,还可以定义监视器检测力;面监视器主要用于监视边界面位置的物理量随时间的变化情况;体监视器主要用于观察计算域内物理量随时间变化的情况
3.6fluent中的压力
FLUENT计算过程中存在诸多的压力,最典型的压力包括静压(Static Pressure)、表压(Gauge Pressure)、动压(Dynamic Pressure)、总压(Total Pressure)、操作压力(Operating Pressure)、相对压力(Relative Pressure)、绝对压力(Absolute Pressure)等。
在FLUENT软件中,涉及压力输入的位置包括:压力入口边界设置,设置入口总压:压力出口边界设置,设置出口静压;操作条件设置,设置操作压力。
4、湍流模型
在流体流动中,主要将流体流动分为层流和湍流。当流速很小时,流体分层流动,互不混合,称为层流,又称稳流或者片流,当流速逐渐增大,流体的流线出现摆动,摆动的频率及振幅随流速的增加而增加,此种称为过渡流;当流速增加到很大时,流线不在清楚可辨,流场中有许多漩涡,层流被破坏相邻流层间不但有滑动,还有混合,这时流体做不规则运动,有垂直于流管轴线方向的分速度产生,这种称为湍流,又称稳流和扰流或乱流。
从流体力学中可知,N-S方程包含一个质量守恒方程和3个动量守恒方程,求解4个物理量,三个速度分量(u,v,w)以及压力p,目前出现的湍流模型都是基于雷诺平均的方法对湍流脉动项进行时间平均处理,进而出现各式各样的湍流模型,但大多数的结果都一样是为了计算出速度及压力。
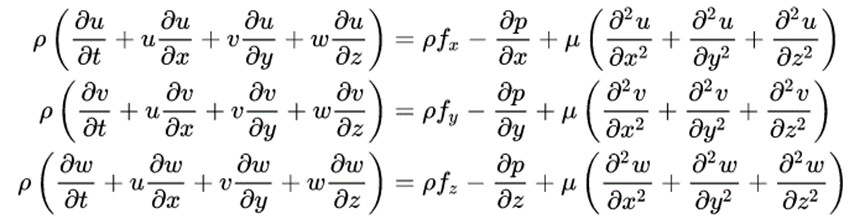
图5.4 直角坐标系下的N-S方程
层流湍流流动
图 5.5 层流湍流流动示例
4.1 湍流和层流的判断
湍流和层流通常用雷诺数来判断
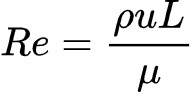
式中,为流体密度,kg/m3;u为流速,m/s;L为特征长度,m;
为动力黏度,Pa s。
对于内部流动,通常认为雷诺数Re高于2300为湍流,低于2300为层流
外部流动,沿表面位置分布的雷诺数Re大于500000时通常认为其为湍流沿障碍物的雷诺数Re大于20000时,认为流动为湍流
对于自然对流,则利用瑞利数与普朗特数的比值进行判断,当满足Ra/Re>10^9时,可认为流动状态为湍流
瑞利数:

普朗特数:
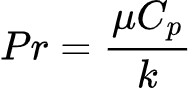
式中,α为热膨胀系数;为温差;
为特征长度;
为运动黏度;k为热导率;
为动力黏度;
为定压比热容。
4.2 湍流求解方法
直接数值模拟(DNS)
从理论上来讲,湍流流动能够由数值方法求解NS方程来模拟,能够求解得到尺寸频率,无需接触额外的模型。但是利用此方法进行求解花费太大(其计算开销随雷诺数成几何倍数增长),因此在工程上的应用受到限制。目前在FLUENT中无法应用DNS方法。
大涡模拟(LES)
由于湍流直接模拟计算开销过大,难以在工业上得到广泛应用,因此在直接模拟的基础上发展出了大涡模拟方法。该方法利用滤波方法,对于大尺度的涡采用直接求解,而对于小尺度的涡则采用RANS方法进行求解。该方法的计算消耗低于DNS,但是对于大多数的实际应用来讲占用的资源还是比较大。随着计算机计算能力的逐渐增强,该方法已经越来越广泛地应用于工业流动计算中。在FLUENT软件中可以使用大涡模拟方法。
雷诺平均NS模型
雷诺平均NS模型(RANS)方法是工业流动计算中使用最为广泛的一种模型,其求解时间均值的纳维斯托克斯方程。在FLUENT软件中,k-e模型、k-w模型以及雷诺应力模型均为RANS模型。
分离涡模型(DES)
分离涡模型是介于大涡模型与RANS模型之间的一种湍流模型。该模型通过比较湍流尺度与网格最大尺寸而自动决定使用大涡模型还是RANS模型进行湍流求解。
4.3、Fluent的湍流模型
如图,在fluent中打开湍流模型设置步骤如下
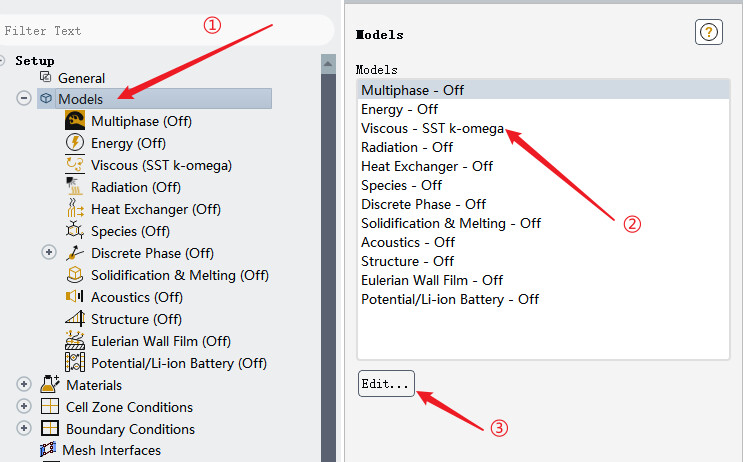
图5.6 在fluent中打开湍流模型设置步骤
主要的模型如Model列所示,下面对其做一定的介绍
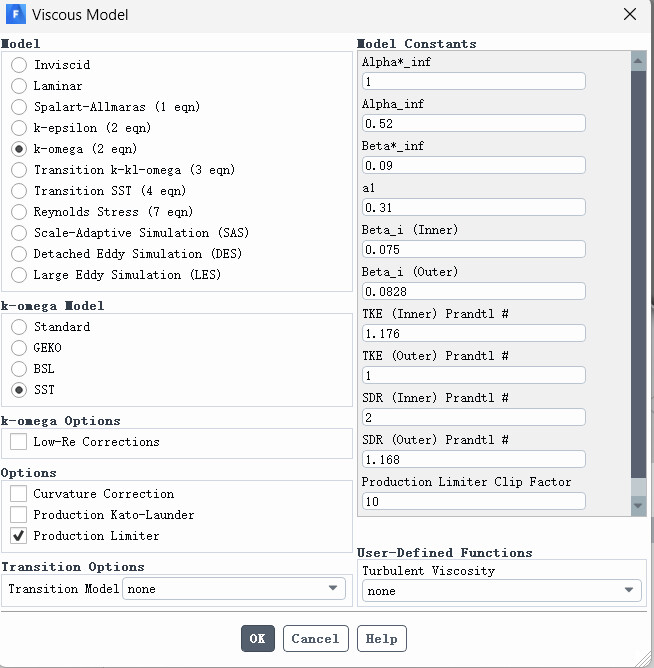
图5.7 主要模型
Inviscid:无黏模型。计算过程中忽略黏性作用,通常应用于黏性力相对于惯性力可忽略的流动。
Laminar:层流模型。默认情况下该模型被选中。计算域内流动状态为层流时采用该模型
Spalart-Allmaras (1 eqn):
SA模型。常用于航空外流场计算。对于几何相对简单的外流场计算非常有效。该方程为单方程模型,比较节省计算资源。
k-epsilon (2 eqn):工业流动计算中应用最为广泛的湍流模型,包括三种形式:标准k-e模型、RNG k-e模型以及Realizable k-e模型。
k-omega (2 eqn):k-w模型也是双方程模型。在Fluent中,它包括两种类型:标准形式以及SSTk-w模型。在对于外流场模拟中,该模型的竞争对手是SA模型。
Transition k-kl-omega(3 eqn):3方程转捩模型,用于模拟层流向湍流的转捩过程。
Transition SST (4 eqn):4方程转捩模型,用于模拟湍流转捩过程。
Reynolds Stress (7 eqn):雷诺应力模型。没有其他RANS模型的各向同性假设,因此适合于强旋流场合。
Scale-Adaptive Simulation(SAS):SAS湍流模型主要用于求解瞬态湍流流动问题。当使用SAS模型时,强烈建议在Solution Methods面板中设置Momentum:选择使用Bounded Centeral Differencing
Detached Eddy Simulation(DES):分离涡模型。当使用分离涡模型时,可选的RANS模型包括Spalart--Allmaras、Realizable k-epsilon以及SSTk-omega模型。
Large Eddy Simulation(LES):大涡模拟模型。在默认情况下,LES模型只在三维模型情况下才可选。若要在2D模型中使用大涡模拟模型,则需要使用TU1命令进行激活。
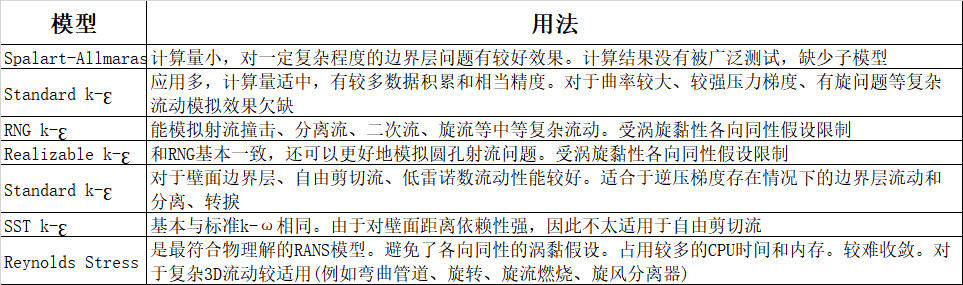
对于在工业流动计算中得到广泛应用的RANS湍流模型,适用场合见表所示
4.4、y+的基本概念
在临近壁面位置,法向速度存在非常大的梯度。在非常小的壁面法向距离内,速度从相对较大的值下降到与壁面速度相同。因此对于该区域内流场的计算,通常采用两种方式:利用壁面函数法;加密网格,利用壁面模型法。对于这两类方法的选取,可以通过y+来体现。
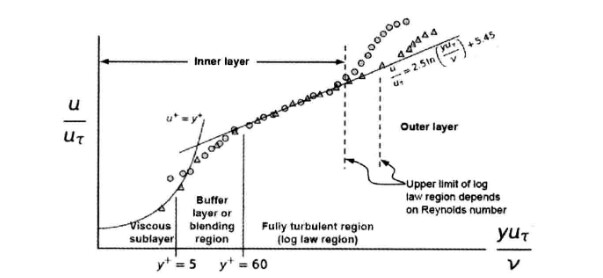
图 5.8 近壁面位置速度分布
图横坐标所表示为无量纲壁面距离
纵坐标为无量纲速度
其中,
为壁面剪切应力,y为壁面法向距离。从图中可以看出,在y+<5的区域,速度呈非线性形式,该区域通常称为黏性子层(Viscoussublayer region);在y+>60区域,速度与距离几乎成线性趋势,该部分区域为完全发展湍流,也称为对数律区域(loglaw region);两部分之间的区域,常称为过渡层(Buffer layer region).
对于近壁区域求解,主要集中在黏性子层的求解上,主要有以下两种方式。
1.求解黏性子层
若想要求解黏性子层,则需要保证+值小于1(建议接近1)。由于y+直接影响第一层网格节点位置,因此对于求解黏性子层的情况,需要非常细密的网格。对于湍流模型,需要选择低雷诺数湍流模型(如k-omega模型)。通常来说,若壁面对于仿真结果非常重要(如气动阻力计算、旋转机械叶片性能等),则需要采用此类方法。
2.利用壁面函数
壁面函数要求第一层网格尺寸满足条件30<y叶<300,当尺寸过小时,壁面函数不可用:当尺寸超出该范围时,无法求解黏性子层。通常使用高雷诺数湍流模型(如标准k-epsilon模型、Realizable k-epsilon模型、RNGk-epsilon模型等)。一般来说,在黏性子层数据不是特别重要的时候可以选用壁面函数进行求解。
3.y+在CFD计算中的应用
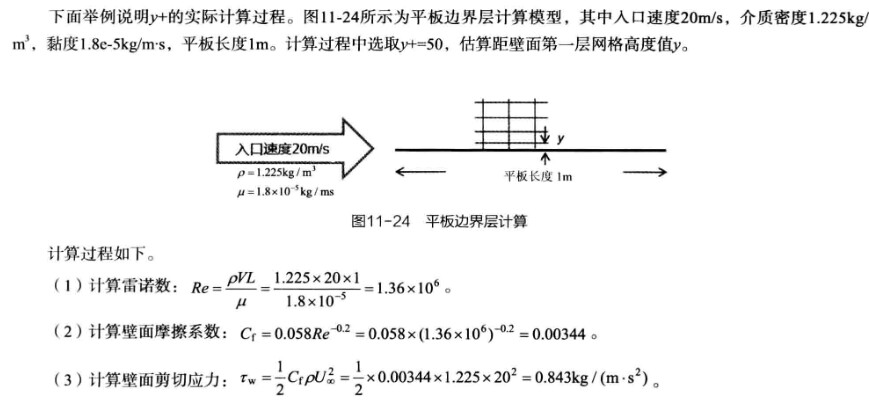
在CFD计算过程中,y+的作用体现在划分网格过程中计算第一层网格节点高度。其计算过程如下。

y+的实际计算过程:

4.5、壁面函数
FLUENT中有5种近壁面处理方法,
这些近壁面处理方法包括标准壁面函数(Standard Wall Functions)、可缩放壁面函数(Scalable Wall Functions)、非平衡壁面函数(Non-Equilibrium Wall Functions)、增强壁面处理(Enhanced Wall Treatment)以及自定义壁面函数(User-Defined Wall Functions).
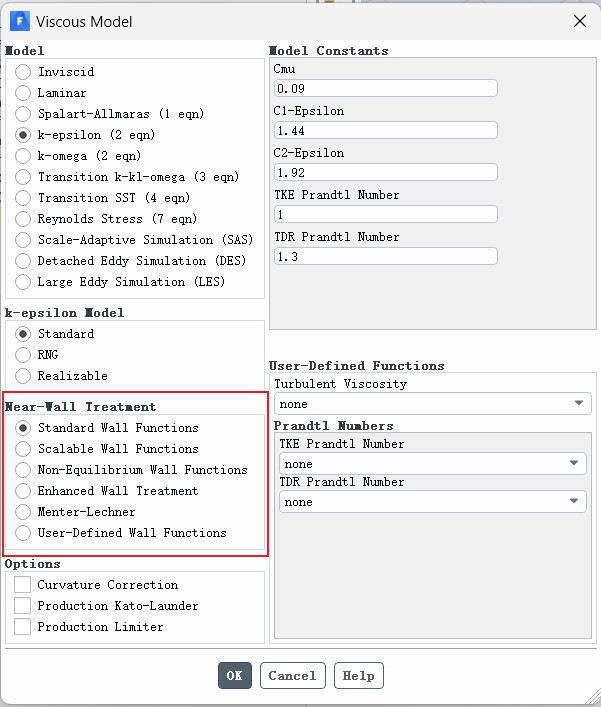
图5.9 近壁面处理方法
这些壁面处理方式中,标准壁面函数、可缩放壁面函数以及非平衡壁面函数均为壁面函数法,适合于高雷诺数湍流模型(k-epsilon模型以及雷诺应力模型),其要求第一层网格节点处于湍流核心区域,即y+值处于30~300之间。而近壁面处理则并非壁面函数法,其适合于低雷诺数湍流模型(k-omega模型),需要在近壁区域划分足够细密的网格,其要求第一层网格节点位于黏性子层内,即y+<5,且要求边界网格层数至少为10~15层。
虽然壁面函数法是一种近似处理方法,然而其在工业流动问题计算中仍然应用非常广泛。对于简单的剪切流动问题,利用标准壁面函数法可以很好地得到解决,而使用非平衡壁面函数法可以对于强压力梯度及分离流动计算进行改善。而可缩放的壁面函数法则可改善第一层网格节点在计算迭代过程中处于黏性子层与核心层之间摇摆从而导致计算不稳定的问题。增强壁面处理通常用于无法应用对数律的复杂流动问题(如非平衡壁面检查层或雷诺数较低的情况下)。近壁面建模的一些推荐策略如下。
(1)对于大多数高雷诺数流动情况(R>10°)下使用标准的或非平衡的壁面函数。在存在分离、再附或者射流流动中常使用非平衡壁面函数法。
(2)对于雷诺数较低或需要求解贴体特征时,需要使用增强壁面处理方法。
(3)增强壁面处理是SA模型与k-omega模型的默认壁面处理方式,但是其也可以用于k-epsilon模型与雷诺应力模型。
5、边界湍流设置
若在计算模型中使用了湍流模型,则在边界条件设置过程中,对于进出口边界需要设定湍流条件,对于不同的湍流模型,在边界设置中湍流组合方式略有不同。若使用了k-epsiloni模型,则在湍流指定方法中可以选择方法K and Epsilon、Intensity and Length Scale、Intensity and Viscosity Ratio以及Intensity andHydraulic Diameter。而若使用了k-omega模型,则湍流指定过程中可以选择K and Epsilon及其他三项。
湍流边界中的一些物理量计算方式如下
1.湍流强度
湍流强度定义为速度脉动的均方根与平均速度的比值。其计算方式如下。
式中,R为雷诺数。例如当雷诺数为50000时,根据式(11-5)计算出湍流强度约为4%。通常I<1%称为低湍流强度,I>10%称为高湍流强度,I=5%通常称为中等湍流强度。
2.湍流尺度(Turbulence Length Scale)
湍流尺度通常用下式进行计算:
式中,L为特征尺寸。
3.湍动能(Turbulent Kinetic Energy)
湍动能可以通过湍流强度及平均速度进行估算:
4.湍流耗散率(Turbulent Dissipation Rate)
湍流耗散率可以利用湍动能、湍流尺寸进行估算:
式中,为k-epsilon模型的经验常数,默认值为0.09。
5.omegai计算(Specific Dissipation Rate)
k-omega湍流模型中的omega可以通过下式进行估算:
式中,k为湍动能;为k-omega模型的经验常数,默认值为0.09。
6.湍流黏度比(Turbulent Viscosity Ratio)
湍流黏度比取值范围通常为1~10。对于雷诺数非常大的内流场,湍流黏度比可能会较大,如可能达到100的量级。
7.水力直径(Hydraulic Diameter)
水力直径可以利用下式进行计算:
式中,A为过流面积;L为湿周长度。
FLUENT边界湍流参数的指定通常采用以上参数的组合,主要包括以下几种方式:显式输人k、epsilon以及omega;Intensity and Length Scale;Intensity and Viscosity Ratio;Intensity and Hydraulic Diameter。这四种组合方式是可相互转换的,通常任意选择一种组合方式即可。用户可以根据计算模型的实际情况,选择最合适的组合方式。
(1)对于内流模型,通常选择湍流强度与水力直径组合。
(2)对于外流场计算模型,可以选择湍流强度与长度尺度组合。
5.1、边界条件分类
边界条件类型主要有以下方面。
(1)axis:轴边界,通常用于旋转几何的2D模型,无需设置边界参数。
(2)outflow:自由出流边界。用于充分发展位置,受回流影响严重,无法应用于可压缩流动模型,也不能与压力边界一起使用。
(3)massflow inlet:质量流量入口边界。设置入口质量流量,通常用于可压缩流动。在不可压缩流动中,通常设置速度入口。
(4)pressure inlet:.压力入口。设置入口位置总压,应用非常广泛。
(5)velocity inlet:速度入口。设置入口速度,通常用于不可压缩流动。设置负速度值可当做出口使用。
(6)symmetry:对称边界。对于2D Symmetry模型,对称轴通常为X轴,模型必须建立在X轴上方。
(7)wall:壁面边界。默认为无滑移光滑壁面,用户可以设置壁面滑移速度。
(8)inlet vent:通风口边界,与压力入口类似,不过需要设置压力损失系数。
(9)intake fan:进气扇边界。与压力入口类似,需要设置总压和压力阶跃。
(10)exhaust fan:排气扇边界。与压力出口类似,需要设置出口表压与压力阶跃。
(11)outlet vent:出风口设置。与压力出口类似,需要设置出口表压与压力损失系数。
(12)pressure far-feld:压力远场边界。通常用于航空航天外流计算中,用于模拟无穷远来流,需要设置马赫数与表压。
(13)fan:风扇边界。为内部双面集总边界(即边界两侧均为同一计算域)。需要定义风扇性能参数。
(l4)interior:内部面边界。通常为计算域内部网格面。无需进行任何设置。
(15)porous jump:多孔阶跃边界。通常需要设置多孔介质的厚度以及压力阶跃系数。
(16)radiator:散热器。需要定义热损失系数及传热效率。
对于以上的边界条件可以简单地分为两类:单面边界及双面边界,见表11-2。单面边界通常指的是几何模型的边界面,而双面边界则通常由内部面转化而来,常常是集总参数边界。

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删