一文教你用优化算法求解工程问题及仿真对比

     优化就是利用各种优化算法求解实际问题的过程。新手在刚开始接触优化问题的时候往往很疑惑，不知道该怎么利用算法解决实际工程问题。今天就结合经典的最速下降法（梯度法）来介绍如何用纯算法进行优化，并将之与optistruct的优化结果进行对比。采用的例子见图1，一个简单的悬臂梁一段被约束，另一端受到垂向力100N，梁尺寸：长1000mm，截面尺寸40X40mm。现在考虑在不增加重量、甚至减重的情况下如何进行优化。

                                      图1 悬臂梁实例

1.最速下降法优化

     1.1 最速下降法介绍

     最速下降法是一种经典的优化算法，该算法利用迭代点处的一阶导数和二阶偏导数，使得每步搜索方向都沿着函数值下降最快的方向（即负梯度方向），因此最速下降法又被称为梯度法。梯度法的优点是开始时步长很大，有利于加快计算速度，迭代过程简单易懂，方法和程序都较为简单，容易实现；但是梯度法每次迭代都是沿迭代点的负梯度方向搜索，相邻两代的搜索方向正交，因此目标函数的性质对收敛速度有极大影响，假设目标函数的等值线与坐标轴正交，两步即可完成收敛，若是斜交，则搜索路径十分曲折，且越是靠近极值点，收敛越慢，因此各大优化软件往往在优化开始时使用最速下降法，达到边界约束时，改用其它算法，如可行方向法，综合各个算法的优点，加快优化进程。

     1.2最速下降法的迭代公式

      首先求解出n维目标函数f在初始点X0的梯度向量：                         

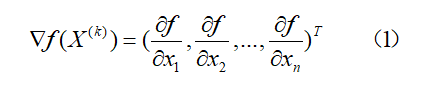
      它是该点函数值增加最快的方向，它的负方向则是函数值下降最快的方向。

      由迭代下降公式：

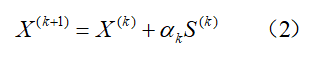
      取搜索方向S(k)为负梯度方向，该方向的单位向量可表示为：

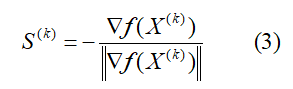
      分母数值代表该点梯度向量的模。

      确定了搜索方向，还需要确定迭代的最优步长，即αk，有两种方法求取αk，一种是利用一维搜索的黄金分割法，另一种是利用泰勒展开式将X(k+1）在X(k)点展开成二次函数求取驻点而得。它的解析式见下式：

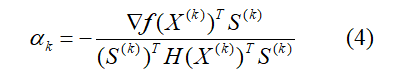
     式中的H矩阵代表X(k)点的Hesse矩阵。

      1.3最速下降法的计算步骤

      1）设定初始点X0,允许误差ξ,迭代代数k=0;

      2）计算迭代点处的梯度和方向；

      3）若满足收敛条件，结束计算，不满足收敛，进入下一步；

      4）计算最优步长αk；

      5）迭代计算得到下一代的点X(k+1)：

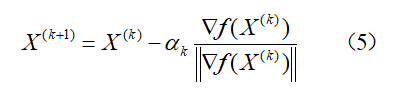
      6)令k=k+1,转步骤2重新计算。

2.建立悬臂梁的优化模型

      2.1结构解析

      悬臂梁一段被完全固定，另一端受到垂向力100N，根据经典材料力学计算公式，其刚度K=3EI/L^3，I=b*h^3/12。

      经计算杆端垂向位移为0.744mm,解析解和有限元计算结果完全一致。现在寻求在不增加重量的情况下，提高该悬臂梁的刚度，从刚度的计算公式可知，减小横截面宽度b，提高截面高度h有利于增加悬臂梁的刚度。

      2.2悬臂梁截面优化模型的建立

      所有的优化问题都要经过转化为数学模型方能利用各种优化算法进行求解。优化数学模型又包含三个要素：

      1）优化变量；

      2）目标函数

      3）约束

     优化变量本例很明了，就是截面尺寸，目标函数是刚度最大，归根结底是让f=b*h^3最大，为了利用基于下降迭代的最速下降法，目标函数可以定义为f的倒数或相反数，此处定义为：g=1/(h^3)*b,之所以将b设立为分子，是因为上文已经分析过，增大截面高度更有利于提高刚度，因此如果截面高度增加，为了减轻质量或维持质量不变，必须减少截面宽度。因此结合实际问题设立合理的目标函数也是利用好优化的一大要点。

      最速下降法的MATLAB实现代码见图2，使用optistruct进行详细优化的过程附在其后。