导读:自9月以来,我的《教你Matlab有限元编程对悬臂梁进行受力分析》原创文章发布以来,我的精品课《Matlab有限元编程从入门到精通》(点击试看)受到了越来越多的工程师朋友的关注,已超过50多人已经订阅学习,欢迎大家加入订阅用户交流群一起讨论Matlab有限元编程那些事(哈哈哈,为大家答疑和分享资料)。
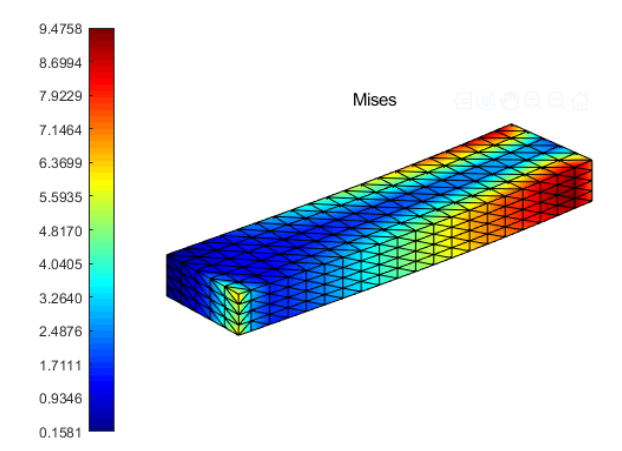
今天,我接着分享Matlab有限元编程专业技能。之前的课程我们学习了一维梁单元,二维平面单元,三维板壳单元的matlab有限元编程,本次案例主要讲解如何用matlab实现针对四面体单元划分的三维结构进行有限元编程,具体案例是一个悬臂梁受集中荷载的问题。图1为本案例Matlab编程计算得到的结果。主要内容涉及四面体单元的有限元基本理论的推导,主要是单元刚度矩阵的推导,此外还包括等参单元和Hammer数值积分以及三维问题的后处理计算。
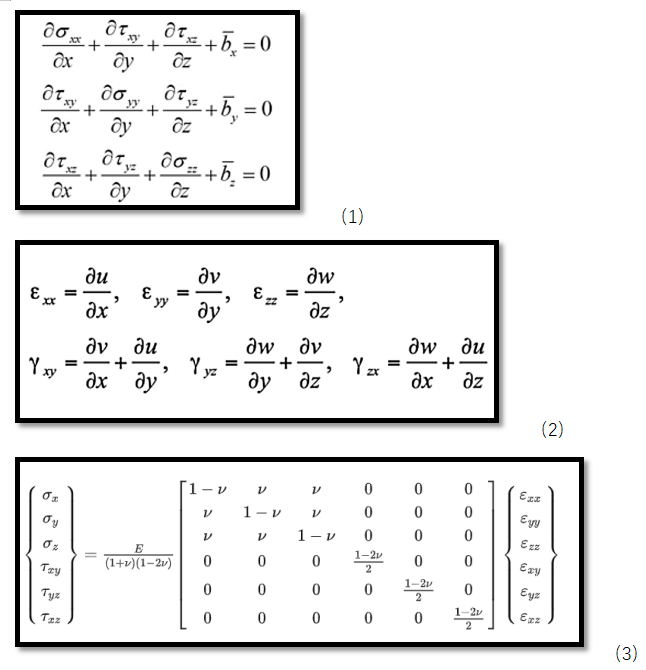
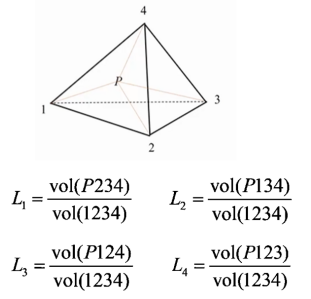
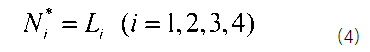
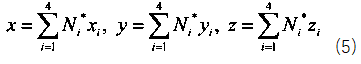
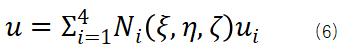
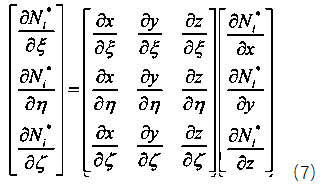
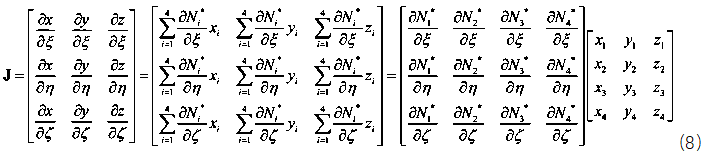
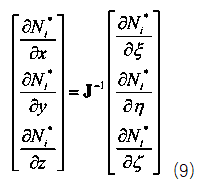
function [NDxyz,JacobiDET] = ShapeFunction(ElementNodeCoordinate)%计算形函数及形函数对局部坐标ksi eta zeta的导数NDL = [-1 1 0 0;-1 0 1 0;-1 0 0 1];%3*4 [N1Dksi N2Dksi N3Dksi N4Dksi;N1Deta N2Deta N3Deta N4Deta……]Jacobi = NDL*ElementNodeCoordinate;%计算雅可比矩阵3*4 4*3JacobiDET = det(Jacobi);%计算雅可比行列式3*3 [DxDksi DyDksi DzDksi;DxDeta……JacobiINV=inv(Jacobi);%对雅可比行列式求逆3*3NDxyz=JacobiINV*NDL;%利用雅可比行列式的逆计算形函数对结构坐标的导数[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……]end这样求出形函数对物理坐标的导数后就可以代入公式(2)几何方程求出应变场矩阵B,经过能量原理的推导可以得到单元刚度矩阵的表达式,注意刚度矩阵的表达式是一个积分的运算,由于被积函数较为复杂,如果代数积分进行计算要消耗大量的计算资源,因此有限元理论中引入数值积分,即我们熟悉的高斯积分和hammer积分,对于直角坐标系我们采用高斯积分,对于面积或者体积坐标系我们采用hammer数值积分,具体这两类积分的原理大家可以参考相关数值积分教材即可,这里我们只利用hammer数值积分的结论。四面体单元具体的数值积分公式如下:
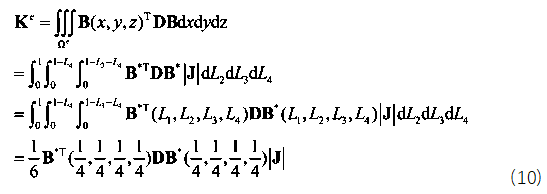
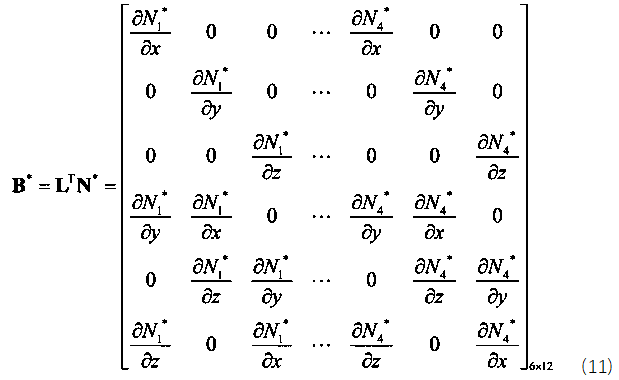
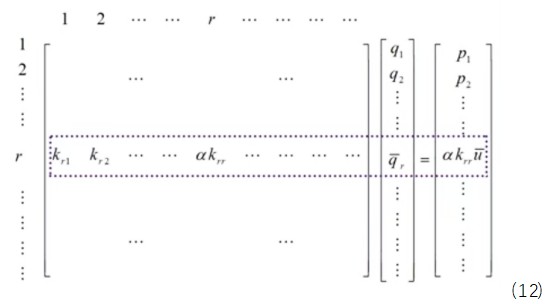
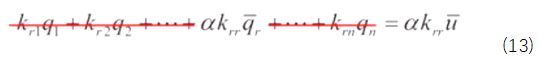
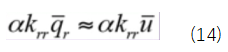
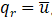

% 计算形函数导数 [NDxyz, ~] = ShapeFunction(ElementNodeCoordinate);%[DN1Dx DN2Dx DN3Dx;DN1Dy DN2Dy DN3Dy;……] ElementNodeDisplacement=U(ElementNodeDOF);%12*1 节点位移列阵 ElementNodeDisplacement=reshape(ElementNodeDisplacement,Dof,4);%3*4 % 计算单元应变 Strain3_3 3*3的应变矩阵 Strain3_3=ElementNodeDisplacement*NDxyz';%高斯积分点处应变 3*4 4*3 %把单元应变矩阵改写成6*1 Strain=[Strain3_3(1,1) Strain3_3(2,2) Strain3_3(3,3) ... Strain3_3(1,2)+Strain3_3(2,1).... Strain3_3(2,3)+Strain3_3(3,2) Strain3_3(1,3)+Strain3_3(3,1)]'; Stress(1:6,1) = D*Strain;%高斯积分点处应变
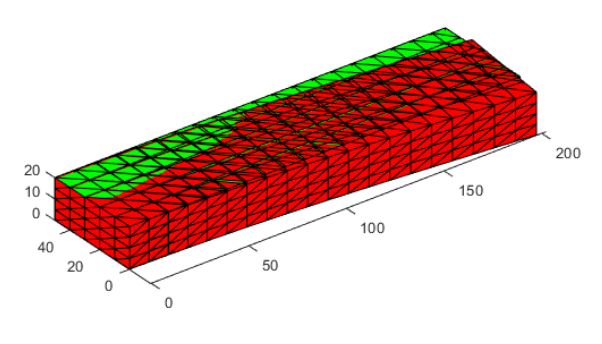 图3 变形前后的网格对比
图3 变形前后的网格对比
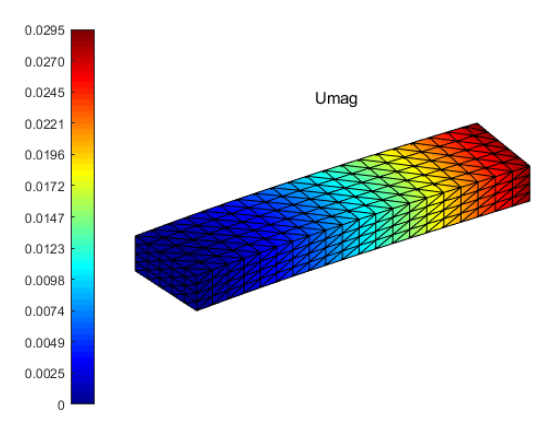 图4 位移云图
图4 位移云图
此外,为帮助大家更好的入门学习Matlab有限元编程分析能力,欢迎大家私信我索要如下 Matlab有限元 资料包。

-
快速获得各典型有限元案例的Matlab代码;
-
学习并掌握有限元基础理论;
-
掌握Matlab编程实现有限元算法的流程;
-
掌握多种有限元单元的基本理论Matlab编程实现过程;
-
掌握静力学、动力学、材料非线性、几何非线性、接触非线性问题的Matlab编程实现;
-
为订阅用户提供知识圈答疑服务,并建立VIP用户交流群,后续可根据订阅用户需求进行加餐直播。此外还提供课程对应的学习资料模型一份。
-
理工科院校学生和教师;
-
学习型仿真设计工程师;
-
Matlab有限元编程兴趣爱好者和应用者。




