VKI高压涡轮叶片湍流隐式大涡模拟技术研究

案例来自陆面体科技公众号。

1 问题描述和流动条件

对VKI高压涡轮叶片[1]进行隐式大涡模拟（ILES）,文献[2]中提供了大量的实验数据。文献[2]中MUR129的流动情况为没有来流湍流。流动参数以SI为单位，雷诺数和马赫数基于等熵出口边界值：

l  进口总压：1.849*10⁵Pa

l  进口总温：409K

l  出口静压：1.16487*10⁵Pa

l  攻角：0

l  基于弦长和出口边界值的雷诺数：1.16*10⁶

l  等熵出口马赫数：0.84

l  普朗特数：0.713

l  气体常数：287.55J/(kg*K)

l  壁面温度：300K

l  粘性系数符合萨瑟兰定律

2 几何和网格参数

l  叶片宽度是弦长的16.6%（0.0676m）；

l  粗网格具有169,750个六面体和278,425个棱柱体单元，其中沿叶片展向有35个单元，如图1所示；

l  网格的平均y +值（来自p2模拟）：3.3；

l  通过将每个单元细分为8个更小的单元生成细网格。

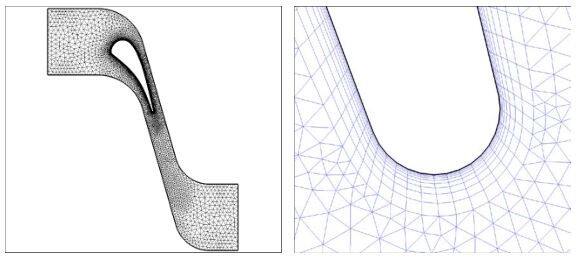
图1 非结构混合网格

3 计算结果

进行网格加密和变精度（p）研究以评估网格和阶次的灵敏度和收敛性。图2显示了不同网格密度和求解阶次下的纹影分布。这些纹影分布清晰地显示了声波、激波，尾迹结构和后缘附近的转棙区。注意到粗网格上的p2模拟具有比细网格上的p1模拟更高的分辨率，表明p细化在解决非定常流动特征方面比网格细化更有效。也可以看出在粗网上转棙区还没有在p2和p3模拟之间完全收敛。粗网格上的p1模拟具有很早的转棙位置，而细网格上的p1模拟具有很晚的转棙位置，p2和p3模拟预测到的转棙位置介于p1粗网格模拟和p2细网格模拟之间。

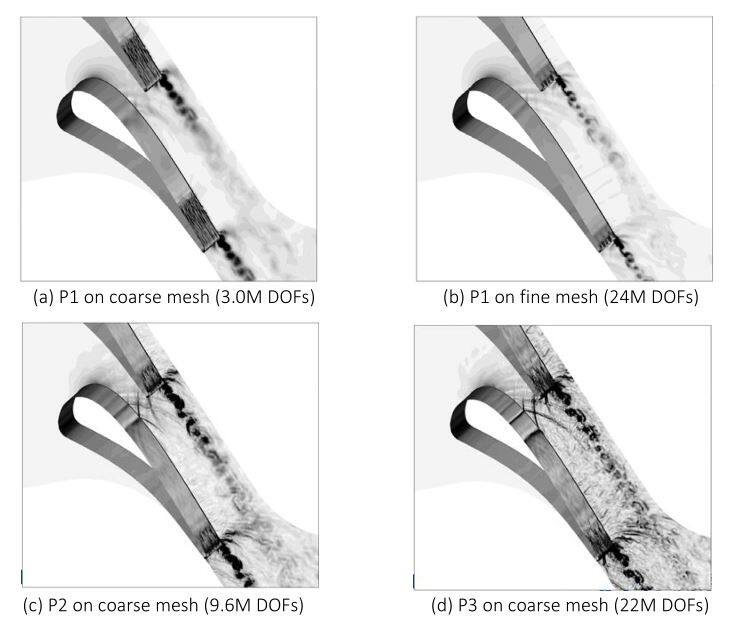
图2 不同多项式次数和网格密度下纹影分布对比图

图3显示了粗网格上不同阶次计解结果的时间平均值。随着多项式次数的增加，收敛性增强。p2模拟和p3模拟结果接近，但p1计算预测的转棙位置较早，而p2计算预测的转棙位置较晚。

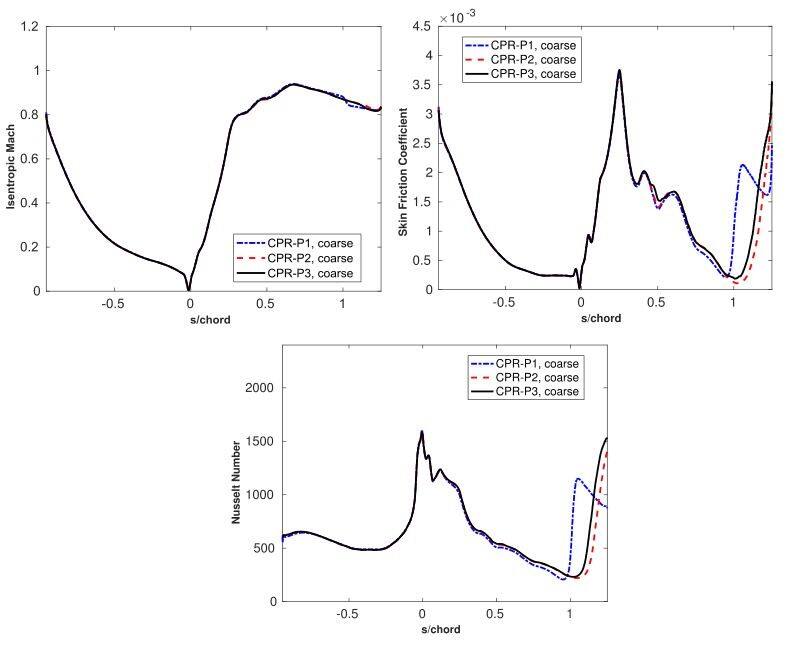
图3 粗网格上p=1,2,3时的载荷和热传递时间平均值计算结果

图4显示了不同阶次的计算结果在后缘附近两个位置处的压力功率谱密度。随着阶次增加，频谱范围更广并趋近Kolmogorov的-5/3法律。

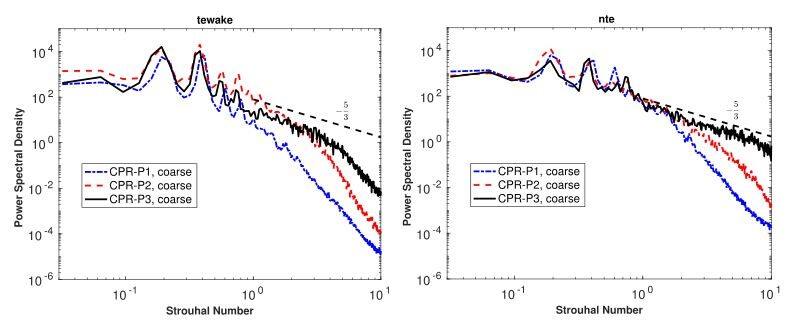
图4 监控点压力功率谱密度

图5显示了细网格上当前模拟数据、实验数据和另一个采用商业软件的模拟数据之间的对比。所有求解器计算的等熵马赫数与实验数据吻合良好，而p3高阶模拟与实验数据最接近。

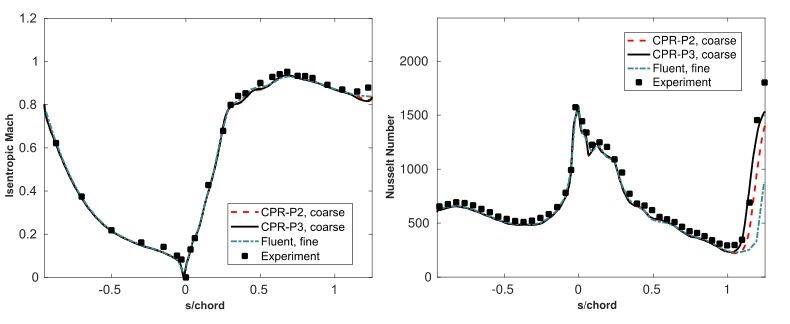
图5 当前模拟、Fluent模拟和实验数据对比

4 仿真详情

l  仿真从p0模拟开始，以便为高阶模拟快速建立合理的初始条件；

l  非定常状态下p1模拟从p0模拟开始，采用BDF2时间积分方法，时间步长为2e-7，运用LUSGS解算器，使用了SMOOTH限制器（mid = -2.5和h_width = 1）；

l  p2模拟从p1结果开始，采用BDF2时间积分方法，时间步长为5.0e-8，运用LUSGS解算器，使用了SMOOTH限制器（mid = -2.0和h_width = 1）；

l  p3模拟从p2结果开始，采用BDF2时间积分方法，时间步长为2.5e-8，运用LUSGS解算器，使用了SMOOTH限制器（mid = -3.5和h_width = 1）；

l  计算资源（Intel Xeon CPU E5-2660, 2.2GHz）：

²  P1：116个CPU核心小时/单位无量纲时间，3M自由度/方程；

²  P2：810个CPU核心小时/单位无量纲时间，9.6M自由度/方程；

²  P2：3300个CPU核心小时/单位无量纲时间，22M自由度/方程。

5 参考文献：

1. Feilin Jia, Jeremy Ims, and Z. J. Wang, James Kopriva and Gregory M. Laskowski, Evaluation of Second- and High-Order Solvers in Wall-Resolved Large-Eddy Simulation, AIAA Journal， Vol. 57, No. 4, April 2019.

2. Arts, T., and Rouvroit, M., “Aero-thermal Performance of a Two-dimensional Highly Loaded  Transonic Turbine Nozzle Guide Vane: A Test Case for Inviscid and Viscous Flow Computations,”  Journal of Turbomachinery, Vol. 114, No. 1, 1992, pp. 147-154.