MATLAB实操经验：思路分享与心得总结

     考虑到大家的时间都很紧张，而且小部分同学对于Matlab软件的操作比较陌生，为了在大学里留下美好的回忆，也为这门实操课增加实践出真知的意义，本文因此撰写思路分享与心得，旨在帮助同学们快速打开思路，节约宝贵时间去做更加有意义的事情。

前排提示：

    本文相关内容仅作参考，切勿奉行拿来主义！激发兴趣和开阔脑洞才是本文的初衷！

前前排提示：

    uu们在看吗？在看正文之前能不能帮我三连一下之前投稿的视频🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️谢谢大家🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️🙇‍♂️

https://space.bilibili.com/51269400

关注一下吧~给个三连吧~

正文

题目一：

前排再提示

由于老师布置作业的那一周我一直忙其他事情，一直到9/15晚上才有空看一眼题目，问题解答也做的比较仓促，所以题目一的建模比较粗糙，没有考虑各种细节，不能保证此解答最为标准；而且我也不太擅长编程，还是初学者，写的代码就很不美观也不优雅，希望有在看的大佬能在评论区提出宝贵的建议🙇‍♂️

1.1我的思路分析，仅供参考

    本题是简单的物理应用题，在着手Matlab代码工作之前，我建议应先在草稿纸上大致列出本题解答的详细过程，画出自己思路的草图，这样在coding中能更有效率的看出什么时候该用哪个变量；

    由于我在物理方面并不处于强项，知识水平停留在高中阶段，因此我对该问只进行了最简单、基本的变量选择，并简化了该物理模型；

位移-路程问题理论分析及假设

  

  这里我主要是以“能量守恒”作为贯穿整个题的核心，因为简化过了模型，所以我认为这应该能符合题目要求；在该基础模型上我有想到若干可以待拓展的方向：

1. 小球质量m 2.重力单位g  3.是否会有空气阻力影响？ 4.小球速度的方向是否会影响它在速度-时间关系图的呈现  5.等等

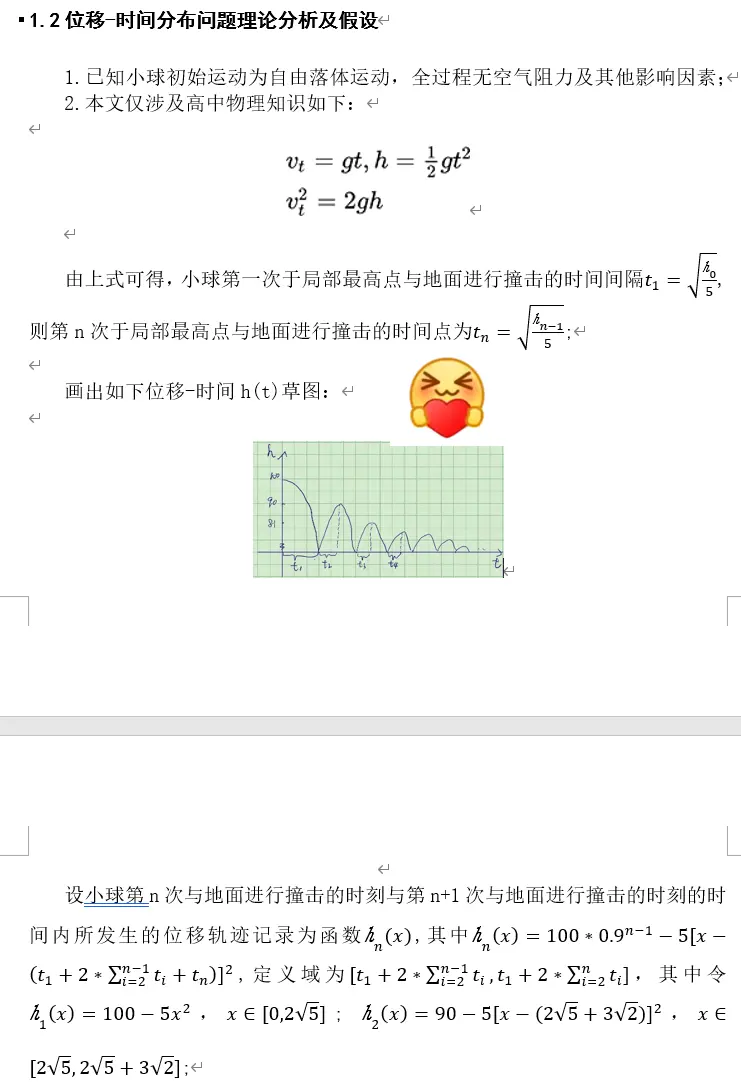
位移-时间分布问题理论分析及假设

例如我在这里画的

这里需要仔细判别每个“周期”函数对应的定义域和函数域！

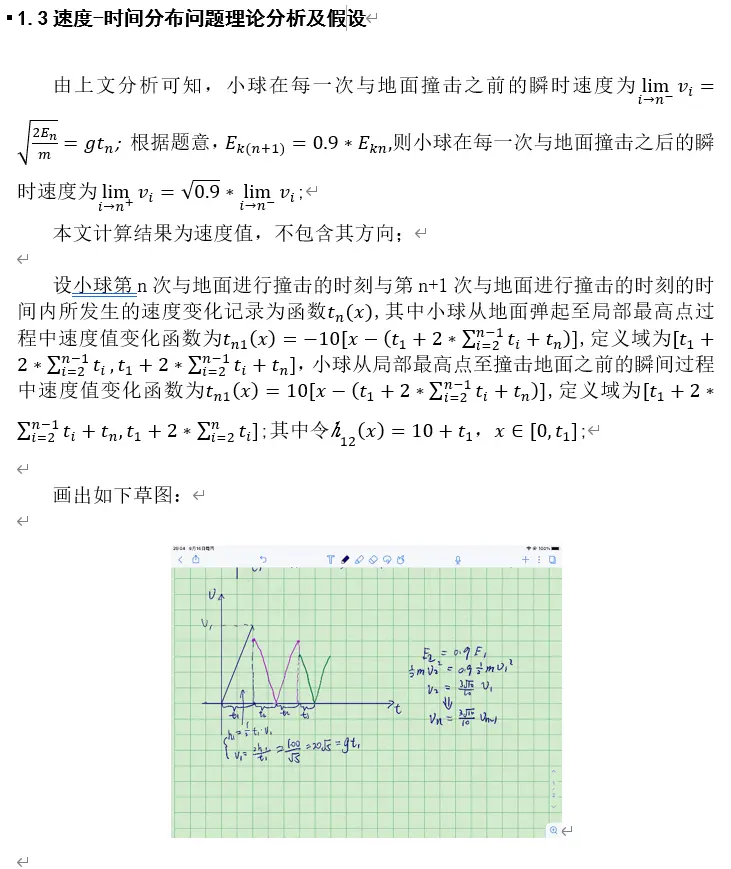
速度-时间分布问题理论分析及假设

同上，该“周期”函数有规律性的定义域和函数域

我觉得这题的每个“周期函数”的定义域和函数域有点像考研数学的数列{an}的证明题，你需要找到an+1和an之间的关系！判断其收敛方向！那么接下来所有的问题都能迎刃而解！（个人解题感想，不一定对，一定不对，对的不一定🤔🤔🤔）

这里我的评价是：想画出对应问题的图像，一定要自己动手先画一下，每个人预设的标准不同，画出来的图也不尽相同！！理清思路，看一下哪一个y点对应上哪一个x点，这样才能为编程提供理论依据！

编程思路方向——加了表情符号的是会有用到的

    该类问题主要的障碍点在于物理公式及推导，在做完如上的工作后，剩下的就是看图说话了：

    给不熟悉matlab的小伙伴讲一下我用到的基础公式及使用实例，大家按这些用法去看图说话，题目便迎刃而解：

    tem = linspace(0,5,n);  % 将[0,5]这个区间等分为n个点（等差数列的形式）

    tem=0:0.1:5; %把[0,5]这个区间分为0,0.1，0.2,0.3，...，4.8,4.9,5.0🤗🤗

  矩阵取值

    A([2,5],:)      %只取第二和第五行（一共两行）

    A(2:5,:)        %取第二到第五行（一共四行，2345）

    A(2:2:5,:)     %取第二和第四行（从2开始，每次递增2个单位，到五结束）

    A(2:end,:)    %取第二到最后一行

    A(2:end-1,:) %取第二到倒数第二行

    A=zeros(m,n) %建立m*n的0矩阵，方便后续在每个位置上填入数字🤗🤗🤗

for循环结构 

循环+求和的组合是本题会用到的 🤗🤗🤗🤗

例题1：

>>sum=0;

>>for i=1:5

        p=1;

               for j=1:i

               p=p*j;

               end

        sum=sum+p;

end

sum

二维平面绘图🤗

pi  ----π

例题一

x=0:0.01:2*pi;

y=sin(x);

figure   %建立一个幕布

plot(x,y)

title ('y=sin(x)')

xlabel('x')

ylabel('sin(x)')

xlim([0 2*pi])    %图像上x值范围

颜色选项参数：

红r  绿g  蓝b  黄y  粉红m  青c   白w   黑k

 

线型选项参数🤗🤗

往往其中的x、y都为一维数组，其实y也就是x对应的函数值，后边的参数用于指定曲线的线形、颜色和数据点标记，如下：

 x = [0:0.01:10]  y = sin(x)  plot(x,y,'-r*')

可以看到，x是一个长度为1001的一维数组，y是和x等长的在sin(x)上的一维数组，后边的-r*分别为曲线线性、颜色、数据点标记，其中参数的一些具体属性如下表所示：

线形\颜色

数据点标记

'-' : 实线

'k' : 黑色

* : 星号

':' : 虚线

b : 蓝色

o : 圆圈

'-.' : 点划线

c : 蓝绿色

s : 方块

'--' : 双划线

g : 绿色

p : 五角星

m : 洋红色

^ : 朝上三角符号

r : 红色

X : 叉

w : 白色

+ : +

y : 黄色

d : 菱形

v : 朝下三角符号

< : 朝左三角符号

> : 朝右三角符号

H : 六角形

详细绘图见网页

https://mp.weixin.qq.com/s?src=11&timestamp=1611664336&ver=2852&signature=L63IFIsEpnl1Jl--h3dQQvfN53bjV6bdr7CJZr3e99vEEzbvKZRPk4qdS3ZKPG0Dq55BDOYL7LKqBg2i3rDY88K-xmYerQPDjnlYseam5NMKBKJVwLlLq7txDt5GM-ai&new=1

***************************************************

绘图标注（以样条插值为例）

Matlab有内置的函数： p = spline (x,y, new_x)  x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

 

例如： x = ‐pi:pi; y = sin(x); new_x = ‐pi:0.1:pi;

p1 = pchip(x,y,new_x); %分段三次埃尔米特插值

p2 = spline(x,y,new_x); %三次样条插值

plot(x,y,'o',new_x,p1,'r‐',new_x,p2,'b‐')🤗🤗

legend('样本点','三次埃尔米特插值','三次样条插值', ‘Location’,‘SouthEast’) %标注显示在东南方向

 

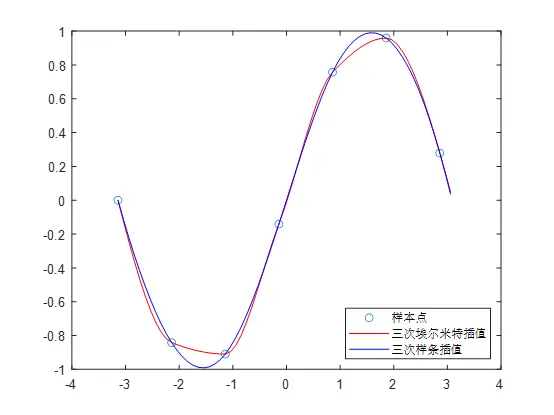
说明： legend(string1,string2,string3, …) 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时 的图标。 ‘Location’用来指定标注显示的位置

    感觉列了这么多你们要打我了，但的确是在我写的时候用上了（一部分，我在图像上没有花功夫去美化），接下来我会列出按上文思路的流程图，让编程方向一目了然：

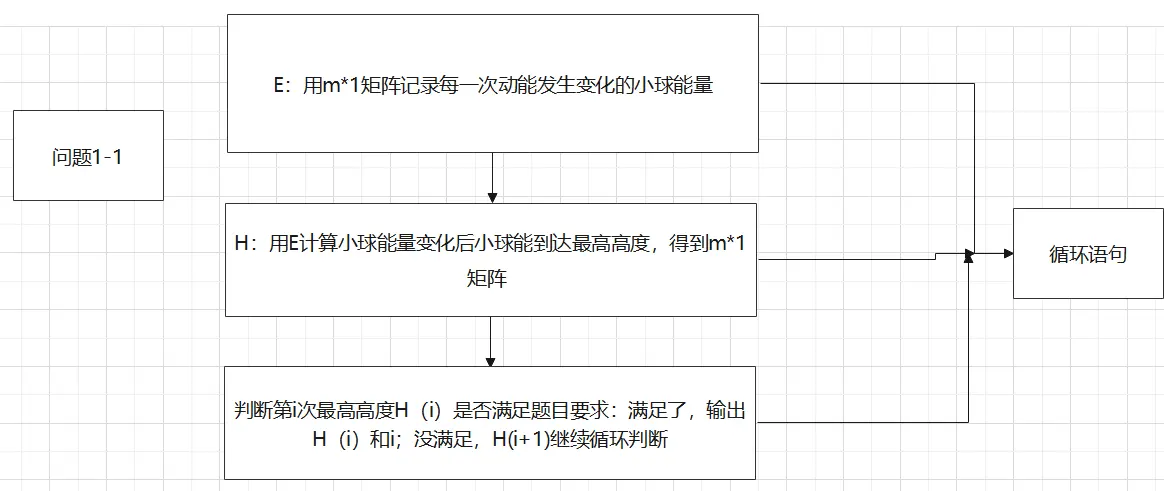
1-1

核心代码及结果图我已发了pyq，大家可以借鉴一下，有更好的操作可以私我一份

 第三问同上，但是按我的思路来看，此题得到的图表为不连续的、分段的函数，大家注意一下，按你们的思路来走！

第二问

本题没有思路，只有搬运！

    这题乍一看很唬人，我也一开始懵逼了，直到我打开老师发的代码里面第二行注释Runge's polynomial interpolation example，我就马上意识到这个是插值问题中的经典问题。

    给大家一个非常好用的参考连接，是该原作者Cleve Moler在The Mathworks上发表的一篇博客：https://blogs.mathworks.com/cleve/2018/12/10，大家一定要看一看，看了一眼就全明白了，就是纸老虎！在评论区我也会给大家链接，里面包含插值定理的基本概念以及该作者新发布的code文件！对完成报告有很大帮助！如果阅读英文文献有障碍，那么在百度直接搜关键词“龙格现象”就能有很多解答思路及其原理！

    我为大家推荐如下链接：

https://zhuanlan.zhihu.com/p/82439672

https://baike.sogou.com/v73855001.htm?fromTitle=%E9%BE%99%E6%A0%BC%E7%8E%B0%E8%B1%A1

https://www.doc88.com/p-1252903560628.html

https://www.zhihu.com/question/39329749/answer/149497977

https://max.book118.com/html/2017/0516/107074067.shtm

都不难的，如果最近有一直复习高数部分的话应该会对原理的理解没有特别大的障碍

代码建议自行按网上教程手打一遍，加深对插值原理的理解

如下是我对原作者Cleve Moler在The Mathworks上发表的一篇博客：https://blogs.mathworks.com/cleve/2018/12/10的搬运翻译，大家想看就看，关键还是要看原博发的函数动态变化图：

Carl Runge（1856-1927）之所以为人熟知，是因为他是第一个写当今称为Runge-Kutta方法的常微分方程数值解的人。他的论文发表于1895年。六年后马丁·库塔（1867-1944）出现在人们的视野。但是Runge做了很多其他的贡献，包括如下的主题。

Runge的顾问KarlWeierstrass的一个经典结果是，对于任何连续函数，有存在收敛的递增阶多项式序列均匀（there exists a sequence of polynomials of increasing order that converge uniformly to the function）。但是这个结果并没有告诉我们多项式是否可以内插或者插值点的位置(whether the polynomials can be interpolating or where the interpolating points might be located.)。

 

Runge著名的插值反例是函数：

f(x) = \frac{1}{1+25x^2}

如果此函数在区间[-1，1]中的等距点上插值，则多项式不一致收敛，最大误差是无限大的。(If this function is interpolated at equally spaced points in the interval [-1,1], the polynomials do not converge uniformly. In fact, the maximum error goes to infinity.)

代码作者Cleve Moler给出三个参数，c, n和w可供调用：c为函数二次项系数；参数n是区间[-11]中的插值点数。插值多项式的阶数是n−1；点的分布涉及到权重w，这些点是等距点和Chebyshev点之间的加权平均值，集中在区间的末尾。

如下作者给出若干不同参数变化下原函数带来的动态变化：（原博有GIF图）

1.当二次项系数c增大时，同时保持等距点的数目不变，目标峰值增大，插值误差增大；

2.当 c不变&点距不变，As n increases, we see the error near the ends of the interval increase dramatically.此结论与上文结论类似，龙格现象明显；

3.增大权重w，其他不变，As we move from equal spacing towards Chebyshev spacing, the error near the end points decreases significantly.龙格现象逐渐消失。

 

同时，作者也给出确定参数组(c,n,w)时函数的静态表现：

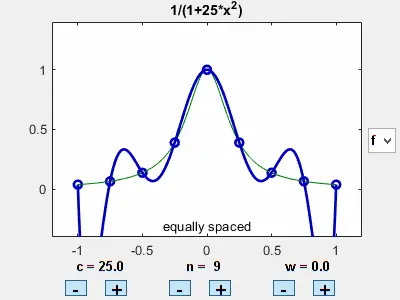
就那样

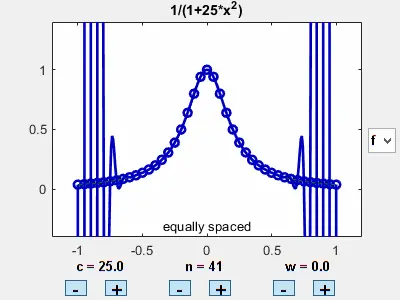
中间拟合的很好，但是两边误差接近无穷大

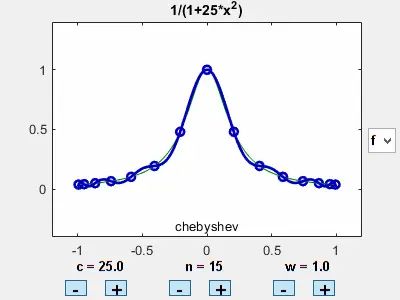
切比雪夫永远的神

结语

拿来主义目标时间规划安排：

题一模型建立参考并创新（1.5h）+代码实现（1h）+题二思考（1h）=3.5h完成

心累，给个三连吧~