信号采样与恢复：MATLAB实验报告与分析

实验说明：

1----验证连续信号和抽样信号

2----验证理想抽样信号的频谱

3----验证频谱混叠的抽样定理

实验过程一：

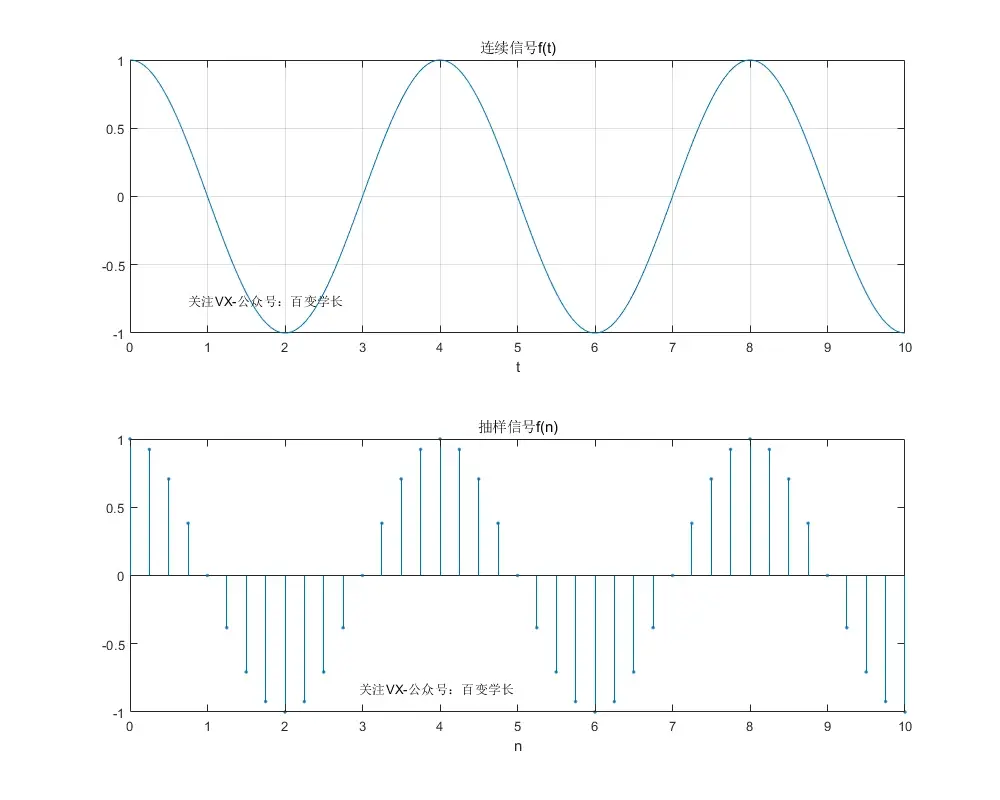
已知一个正弦信号：f(t)=cos(0.5*pi*t),抽样周期为Ts=1/4s，用Matlab绘制信号f(t)和抽样f(n)的波形图；

实验结果示意图： 在这个实验的例子当中，程序首先将连续时间t进行离散化，使之成为以Ts=1/4s的离散时间n，然后将n带入信号x(t)的数学表达式当中进行计算； 以此来完成整个信号的抽样过程，而且得到了抽样后的离散时间序列x(n)的信号波形示意图；

实验过程二： 

实验结果示意图：

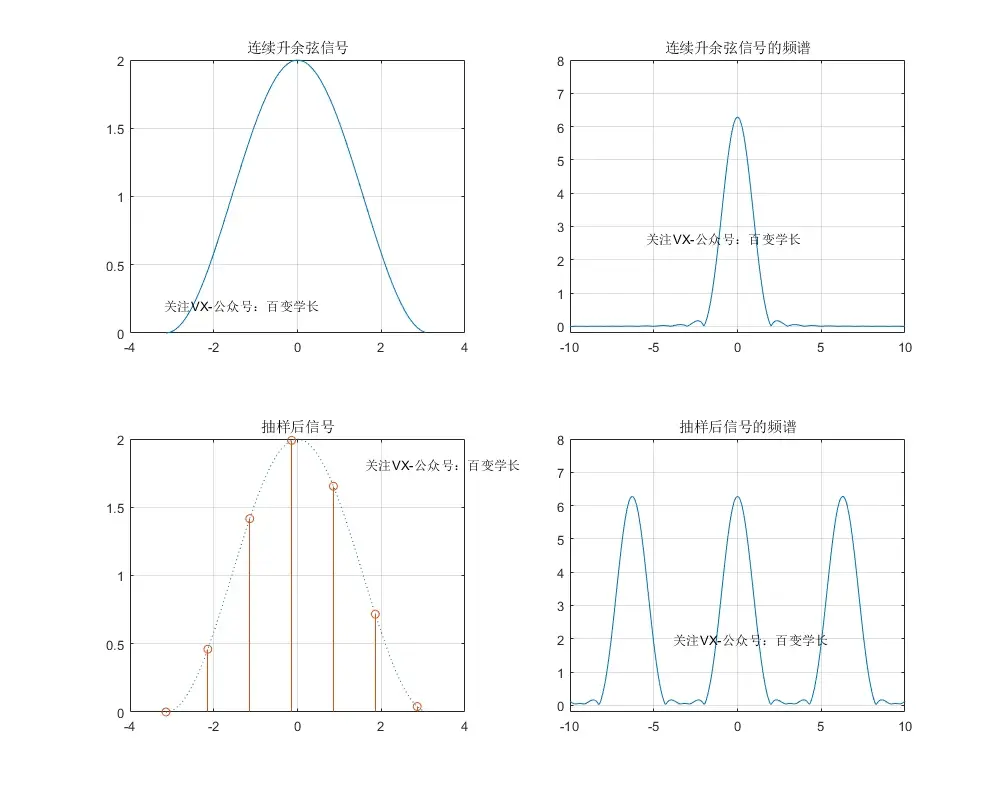
实验结果分析：

从升余弦脉冲信号的频谱抽样后发生了周期延拓，频域上面周期为Ws = 2*pi/Ts。 频谱能量集中分布在w=[0 2]区间内；

实验过程三：

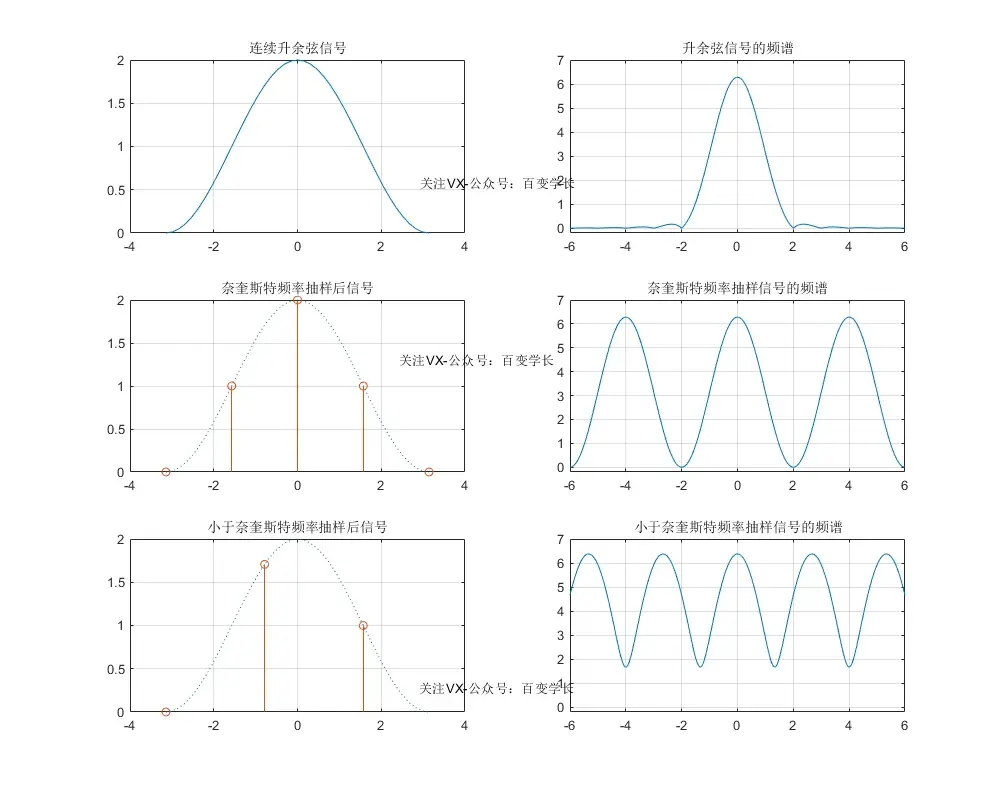
实验结论分析：

程序运行结果如上图所示。由图可见，升余弦信号的频谱抽样后发生了周期延拓； 当为奈奎斯特频率抽样之后，信号的频谱不会发生混叠； 当抽样频率小于奈奎斯特频率时，频谱会发生混叠失真； 本次实验可以用来观察在不同的抽样频率条件下已抽样信号频谱的混叠程度， 从而更加牢固的理解抽样定理； 

实验过程四：

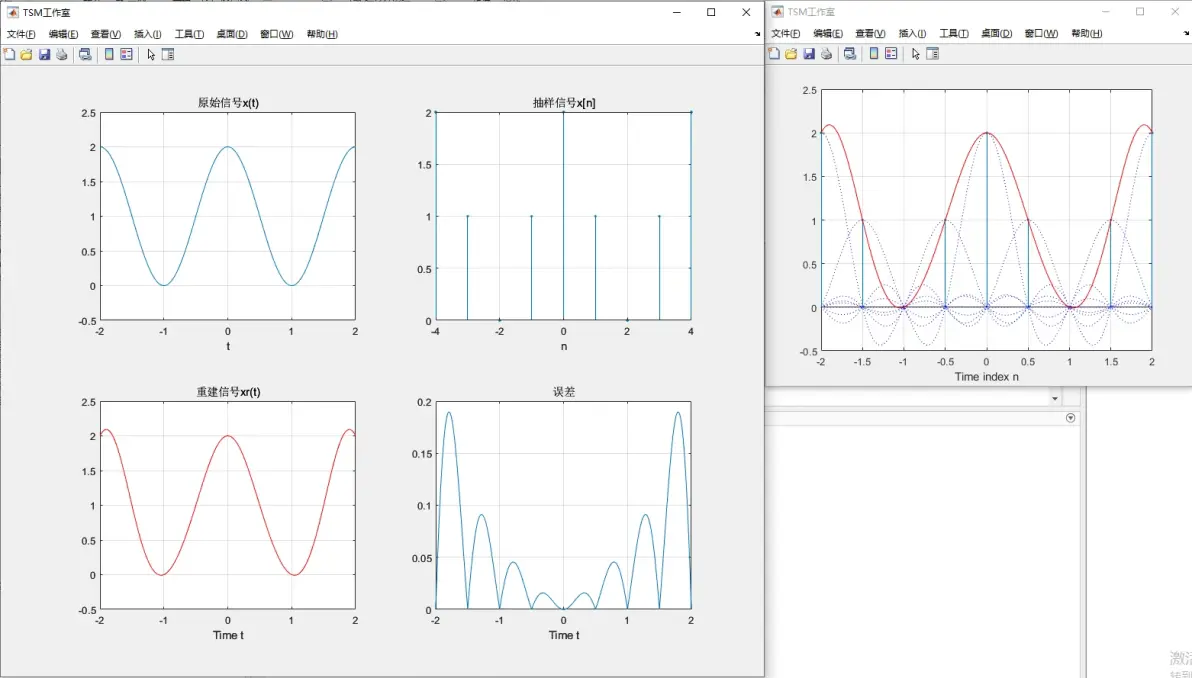
实验目的：信号重建

实验原理： 信号重建是指从采样信号中还原原始连续信号的过程。在信号采样中，连续信号在时间上进行离散化，转换为离散时间信号。

信号重建的目标是通过采样信号来还原原始连续信号，以便进行进一步的处理或分析。 信号重建原理基于采样定理，也称为奈奎斯特定理。奈奎斯特定理指出，要完全重建一个带限信号，就需要对信号进行至少两倍带宽的采样频率。 具体而言，如果一个信号的最高频率为B，则它的采样频率必须大于或等于2B才能完全还原原始信号。

在信号重建中，常用的重建方法是插值。插值是通过在采样点之间插入新的采样点来还原连续信号。 最简单的插值方法是线性插值，它假设采样点之间的信号变化是线性的。更高阶的插值方法如样条插值或多项式插值可以提供更精确的重建结果。 除了插值，信号重建还可以使用一些信号处理技术，如滤波和谱估计。

滤波可以去除采样过程中引入的混叠和噪声，以减小重建误差。 谱估计可以通过分析采样信号的频谱信息来还原原始信号的频谱特性。 需要注意的是，信号重建并非总能完全还原原始连续信号。采样定理只能保证在满足一定条件下对信号进行完全重建。

如果采样频率不足以满足奈奎斯特定理的要求，将引入采样误差，并可能导致重建信号中的混叠现象。因此，在进行信号采样时，需要根据信号的频率特性和重建需求来选择合适的采样频率。

实验题目：

已知升余弦信号f(t)=1+cos(pi*t),0=<|t|=<2,利用不同抽样周期Ts进行理想抽样，并进行重建；

实验结果：

程序运行结果：根据不同的抽样频率，得到不同的结果图。 运行过程中出现暂停，可以按任意按键继续程序运行，从而方便观察其重建过程以及结果；

实验波形图：