循环码的定义:
一个(n, k)线性分组码,若将其任意一个码字的码元向右或向左循环移一位,所得的或仍然是码字,则称该码为循环码。如果该码同时也是系统码,那么称为系统循环码。
生成多项式:
在(n,k)循环码的2^k个码字中,取一个前k-1位皆为0的码字,此码字对应有一个次数最低,且为n-k=r的多项式g(x),其它码字所对应的码多项式都是g(x)的倍式,则称g(x)生成该码,并且称g(x)为该码的生成多项式。由生成多项式可以得到循环码的所有许用码字。
1.1、编码过程
由生成多项式得到系统循环码的具体方法如下:
(1).将信息多项式m(x)预乘x^(n-k),即右移(n-k)位,移位后的进位位置补零。
(2).将x^(n-k)·m(x)除以g(x),得到余式r(x)。
(3).系统循环码的码多项式可写成C(x)=x^(n-k)·m(x)+r(x)
1.2、解码原理
设R(x)为接收码字多项式,E(x)为差错图样多项式,S(x)为伴随式,则根据循环码的性质有以下结论:
S(x)=Rg(x)[R(x)]=Rg(x)[E(x)]
当R(x)=C(x)时,有E(x)=0,S(x)=0
当R(x)≠C(x)时,E(x)≠0,S(x)≠0
可通过计算每一种可能被纠正的错误图样E(x)的伴随式,Si(x)=Rg(x)[E(x)],将结果一一对应保存起来,用作译码时查表纠错。
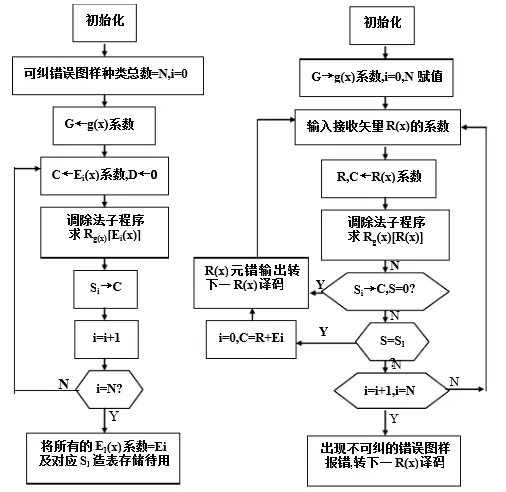
纠错表生成与纠错译码流程图
MATLAB代码实现
clc;clear;close all;
% 以下为(10,6)循环码,g=x4+x+1生成的码组,一位发生错误后打表程序
tab = zeros(1,10);
for i =1:10
E = [0 0 0 0 0 0 0 0 0 1];
E = circshift(E',i)';
x_r = [1 1 0 0 0 0 1 1 1 1];
x_r = double(xor(x_r,E));
g = [1,0,0,1,1];
r_g = gf(x_r,1); % r_g为接收码字的二元域形式r(x)
g_g = gf(g,1); % 生成多项式向量的二元域形式g(x)
% 用r(x)除以生成多项式g(x),得出余式即校验子多项式s(x),
[~,s_g] = deconv(r_g,g_g);
s = s_g.x;
tab(11-i)= s(7)*8+s(8)*4+s(9)*2+s(10);
end
clc;clear;close all;
N=1000;
x = randi(64,1,N)-1;%生成N个随机数列
x_bit = reshape((de2bi(x))',1,6*N); %转换为二进制信息流,长度为N*6
g = [1,0,0,1,1]; %生成多项式
x_encode = cyclic_enco(x_bit,g);%编码序列
SER_sum = zeros(1,1000);
Pe = linspace(0.01,0.5,1000);
for i = 1:1000
%差错图谱
E = randsrc(1,length(x_encode),[[0,1];[1-Pe(i),Pe(i)]]);
%根据差错图谱得到实际接收码字
x_r = double(xor(x_encode,E));
%译码
x_decode = cyclic_deco(x_r,g);
%计算误码率
x1 = bi2de(reshape(x_decode,6,N)')';
SER = sum(x1~=x)/N;
SER_sum(i) = SER;
end
plot(Pe,SER_sum)
title('错误概率与误码率曲线');xlabel('Pe');ylabel('SER')
% 绘制直接传输时的误码率图用作对比
for i = 1:1000
%差错图谱
E = randsrc(1,length(x_bit),[[0,1];[1-Pe(i),Pe(i)]]);
%根据差错图谱得到实际接收码字
x_r = double(xor(x_bit,E));
x1 = bi2de(reshape(x_r,6,N)')';
SER = sum(x1~=x)/N;
SER_sum(i) = SER;
end
hold on
plot(Pe,SER_sum)
legend('循环码','直接传输');
function [ code_out ] = cyclic_enco(x,g)
%(10,6)循环码编码
%输入原序列x,生成多项式g
% 系统循环码编码的原理是,首先用x^r乘以信息码字多项式m(x),这里r = 4;然后用x^r*m(x)除以生成多项式g(x),
% 得余式r(x);最后得系统循环码多项式c(x) = x^r*m(x) + r(x)
code_out = zeros(1,length(x)/6*10);
for i=1:length(x)/6
x_code = [x(6*i-5:6*i),zeros(1,4)]; % 在信息码字后面补上4个零,相当于乘上x^r
% 把信息码字多项式向量和生成多项式向量转到二元域GF(2)上,函数gf(X,M)用于从向量X生成GF(2^M)上对应的向量
x_g = gf(x_code,1);
gen_g = gf(g,1);
% 用x^r*m(x)除以生成多项式g(x)
[~,rem_g] = deconv(x_g,gen_g); % 在Matlab中,多项式除法等同于解卷积运算
rem = rem_g.x; % rem_g.x表示二元域向量rem_g的一个属性,即多项式的系数。注意rem_g.x是在实数域中,而rem_g是在二元域中
% 输出系统循环码
code_out(10*i-9:10*i) = [x(6*i-5:6*i),rem(7:10)];
end
end
function [ decode_out ] = cyclic_deco(x_r,g)
%(10,6)系统循环码译码器
decode_out = zeros(1,length(x_r)/10*6);
for i=1:length(x_r)/10
x_code = x_r(10*i-9:10*i);
r_g = gf(x_code,1); % r_g为接收码字的二元域形式r(x)
g_g = gf(g,1); % 生成多项式向量的二元域形式g(x)
% 用r(x)除以生成多项式g(x),得出余式即校验子多项式s(x),
[~,s_g] = deconv(r_g,g_g);
s = s_g.x;
% 查表求错误图样
switch s(7)*8+s(8)*4+s(9)*2+s(10) % s[1..10]的后四位是理论上的余式;因为case语句不接受向量参数,所以把校验子向量按二进制转化为标量
case 0
e = 0; % e表示错误的位置,如果e为零,则表示没有错误
case 1
e = 1; % 第一位错,以下类推
case 2
e = 2;
case 4
e = 3;
case 8
e = 4;
case 3
e = 5;
case 6
e = 6;
case 12
e = 7;
case 11
e = 8;
case 5
e = 9;
case 10
e = 10;
otherwise
e = 0;% disp('检测出错误,但无法纠正');
end
if e~=0
E = [0 0 0 0 0 0 0 0 0 1];
E = circshift(E',11-e)';
x_code = double(xor(x_code,E));
end
decode_out(6*i-5:6*i) = x_code(1:6);
end
end

(以上代码循环遍历了不同误码率情况下循环纠错码与直接传输之间的误码率,用作分析对比,故而运行较慢,仅需要实现编码与译码请删除该部分)
(该例程实现为(10,4)循环码,需要其他循环码可以修改生成多项式与纠错码表实现)