文中的代码测试环境为MATLAB R2019a,CPU为Intel 8700,睿频至4.3GHz。
对于MATLAB新手来说,这是最容易犯的错误之一。
MATLAB中的数组在使用之前不需要明确地定义和指定维数。当赋值的元素下标超出现有的维数时,MATLAB 就为该数组或矩阵扩维一次,这样就会大大降低程序的执行效率。因此,在循环前,预分配内存,可以有效提高程序执行速度。
function test
fprintf('f1 is finished in %.4f second.\n',timeit(@f1));
fprintf('f1_pro is finished in %.4f second.\n',timeit(@f1_pro));
% f1 is finished in 3.0272 second.
% f1_pro is finished in 0.0571 second.
end
function A = f1
for ii = 1:1e3
for jj = 1:1e4
A(ii,jj) = ii + jj;
end
end
end
function B = f1_pro
B = zeros(1e3,1e4);
for ii = 1:1e3
for jj = 1:1e4
B(ii,jj) = ii + jj;
end
end
end这种低级错误在循环次数很大时,运行时间会成倍增长。
MATLAB大部分内置函数是m文件,本身也是MATLAB程序,执行效率较低。但有一部分底层的基本函数是built-in函数,执行效率更高,如sum、max、find、exp、fft等等,优先使用built-in函数能够获得更快的执行速度。
一个例子是sum和mean函数,求数组平均值时,sum之后除以数组长度比直接调用mean函数快。
function test
A = randn(1e4,1e5);
fprintf('f2 is finished in %.4f second.\n',timeit(@()f2(A)));
fprintf('f2_pro is finished in %.4f second.\n',timeit(@()f2_pro(A)));
%f2 is finished in 0.4895 second.
%f2_pro is finished in 0.4875 second.
end
function [B,C] = f2(A)
B = mean(A,1);
C = mean(A,2);
end
function [B,C] = f2_pro(A)
B = sum(A,1)/size(A,1);
C = sum(A,2)/size(A,2);
end判断一个函数是否是built-in function最直接的手段就是执行edit命令,如
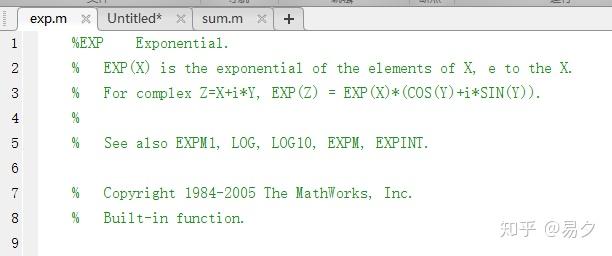
edit exp编辑器会打开exp.m文件,里面没有代码,只有注释,清楚的写明这是一个built-in函数。
MATLAB继承了Fortan按列储存的特点,意味着按列计算时,内存命中率更高,速度更快。
function test
A = randn(1e4,1e4);
fprintf('f3 is finished in %.4f second.\n',timeit(@()f3(A)));
fprintf('f3_pro is finished in %.4f second.\n',timeit(@()f3_pro(A)));
% f3 is finished in 0.7349 second.
% f3_pro is finished in 0.3419 second.
end
function B = f3(A)
B = fft(A,[],2);
end
function B = f3_pro(A)
B = fft(A,[],1);
end上述例子中,对矩阵按列做fft,比按行做fft快一倍。
MATLAB调用函数时,需要搜索该函数并进行匹配,搜索的优先级按照如下:
可以看到,搜索时,文件夹内的函数优先级时很低的,如果改用局部函数,则会更快地搜索该函数。
function test
A = randn(1e4,1e4);
fprintf('f4 is finished in %.4f second.\n',timeit(@()f4(A)));
fprintf('f4_pro is finished in %.4f second.\n',timeit(@()f4_pro(A)));
% f4 is finished in 4.2265 second.
% f4_pro is finished in 2.4430 second.
end
function B = f4(A)
for ii = 1:size(A,1)
for jj = 1:size(A,2)
B = myFun(A(ii,jj)); %myFun函数与localFun函数内容一致,但位于文件夹内的myFun.m中
end
end
end
function B = f4_pro(A)
for ii = 1:size(A,1)
for jj = 1:size(A,2)
B = localFun(A(ii,jj));
end
end
end
function y= localFun(x)
y = abs(x);
end一个矩阵中,如果只有少量的非0值,则可以将其用稀疏矩阵来表示。稀疏矩阵仅记录了矩阵中的非0值。当矩阵的稀疏度足够大时,将矩阵转化成稀疏矩阵,可以降低内存占用空间,同时减少计算量。
function test
A = diag(1:1e4); % A占用内存约800MB
fprintf('f5 (full matrix) is finished in %.4f second.\n',timeit(@()f5(A)));
B = sparse(A); % B占用内存约240KB
fprintf('f5 (sparse matrix) is finished in %.4f second.\n',timeit(@()f5(B)));
% f5 (full matrix) is finished in 0.0246 second.
% f5 (sparse matrix) is finished in 0.0000 second.
end注意:若矩阵的稀疏度不大,强行转换成稀疏矩阵反而会导致内存占用空间变大,执行效率降低。
在新版本的MATLAB中,for循环的执行效率得到很大的提高,但是对于在for循环中进行一些复杂的操作,比如在for循环中改变数组的维数,向量化仍是提升MATLAB执行效率的有效手段。
这里举一个例子,有一个1e6*1的数组A,现在需要去掉数组中索引为1e3的倍数的数,形成一个9.99e5*1的数组。
function test
A = randn(1e6,1);
fprintf('f6 is finished in %.4f second.\n',timeit(@()f6(A)));
fprintf('f6_pro is finished in %.4f second.\n',timeit(@()f6_pro(A)));
% f6 is finished in 4.7358 second.
% f6_pro is finished in 0.0049 second.
end
function A = f6(A)
for ii = 1:numel(A)/1000
A(ii*999+1) = [];
end
end
% 时间已过 5.909668 秒
function A = f6_pro(A)
A = reshape(A,1000,[]);
A(end,:) = [];
A = A(:);
end更新:为何不直接写成A(1e3:1e3:end)=[]的形式,主要是因为MATLAB对大数索引的效率比较低。这里也做一个对比。
function test
A = randn(1e8,1);
fprintf('f6_pro is finished in %.4f second.\n',timeit(@()f6_pro(A)));
fprintf('f6_extra is finished in %.4f second.\n',timeit(@()f6_extra(A)));
% f6_pro is finished in 0.5674 second.
% f6_extra is finished in 0.8525 second.
end
function A = f6_pro(A)
A = reshape(A,1000,[]);
A(end,:) = [];
A = A(:);
end
function A = f6_extra(A)
A(1e3:1e3:end) = [];
end免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删