产品
以后会有视频课程讲解,敬请期待。
简介
蒙特卡罗法本质:当无法求得精确解时,进行随机抽样,根据统计试验求近似解。
通俗理解:
简单例题
圆周率π没有精确值,如何求出其近似值?`
1、什么时候会用到π?求面积的时候;如果能求到面积的近似值,自然能求得π的近似值;
3、一个半径为1的圆,与其相关的其外切正方形面积有精确值4;
4、若在正方形内随机撒大量的点,有些落在圆内,有些落在圆外;
5、统计意义上,圆内点数 / 总点数 = 圆面积 / 正方形面积;
6、第5条中有3项是有统计值或精确值的,所以可求出“圆面积”的统计意义值即近似值
7、圆面积S = π*(r^2),基于前6条即可求出π的近似值
MATLAB代码实现
clc;clear
%蒙特卡洛算法求解圆周率近似值
% 参数初始化:投放10000个点,圆半径为1,圆心坐标(0,0)
% 初始时还未投放点,有0个点在圆内
p = 10000; r = 1; x0 = 1; y0 = 1; n = 0;
% 将p个点随机放在一个边长为2的正方形内,该正方形内有个内切圆
% 正方形的面积是4
% 因为每个点都是“随机投放”的,最终落在圆内的点数比上总点数,就近似等于圆的面积比上正方形面积
% 即pi*(r^2)/4 = (圆内点数)/(总点数)
hold on % 保持绘图窗口,多次绘图
for i = 1:p % 对于要投放的总共p个点
% rand函数产生在(0, 1)之间的随机数;rand函数还有其他多种形式,可自行百度
px = rand*2; % 随机生成该点的横坐标
py = rand*2; % 随机生成该点的纵坐标
% 所以,
% 若该点在圆内,则颜色设为蓝色,变量n加一;在圆外则设为红色
if (px-1)^2 + (py-1)^2 < 1 % 横纵坐标的平方和小于半径,则在圆内
plot(px,py,'.','Color',"b");
n = n+1;
else
plot(px,py,'.','Color',"r");
end
end
axis equal % 绘图时横纵坐标单位长度相同,便于观察圆
s = (n/p)*4;
pi0 = s;
% 注意:matlab本身有圆周率值,在计算时直接调用pi即可
% a = 2*pi结果:
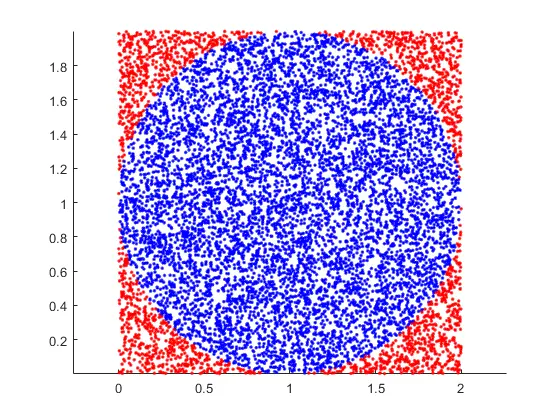
求得的近似值为3.1420。
重点
随机性:matlab中的rand函数,rand(n)意味着生成n个介于0到1的随机数
统计性:n要足够大,太少的话不构成统计意义
近似解:并不是严格的精确解。如果有求精确解的方法,就不要求近似!!!

关注公众号:数学建模BOOM,在后台回复
回复 “群”,获得交流群群号,课件在群文件
回复“最新资料”,免费领取超全数模资料
(注意是去公众号回复,不是b站本账号~)