logistic回归是一个用于二分分类的算法。
例子:假如你有一张图片作为输入,想要输出识别此图的标签,是猫则为1,不是则为0。用y来表示输出的结果标签。
图片在计算机中是如何表示的呢?计算机保存一张图片,要保存成三个独立的矩阵,分别对应图片中红绿蓝三个颜色通道。所以如果图片像素为64*64,则就有三个64*64的矩阵,分别表示像素中红绿蓝三种颜色的亮度。
给一个5*4(高*宽)规模的矩阵作为例子,要把这些像素亮度值放进一个特征向量中,就要把这些像素值都提出来,放入一个特征向量x。定义一个特征向量x,先将红色的像素强度值列出来,然后列绿色、蓝色,全部列成一长列,把图片中所有的红绿蓝像素强度值都列出来。所以如果图片是64*64像素,则特征向量x的的总维度是64*64*3=12288。nx表示特征向量x的维度,为了简洁,用n表示。
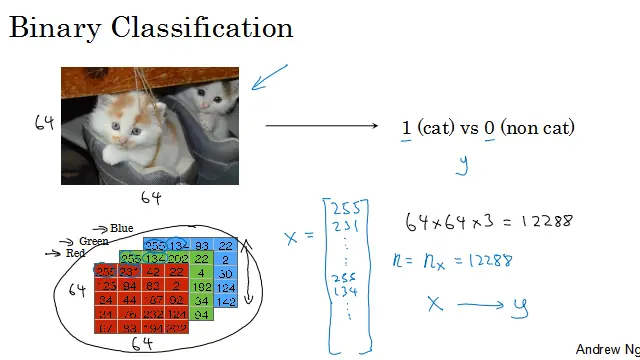
在二分分类问题中,目标是训练出一个分类器。它以图片的特征向量x作为输入,预测输出的结果标签y是1还是0,也就是预测图片中是否有猫。
符号约定:用一对(x,y)来表示一个单独的样本,x是nx维的特征向量,y是标签,值为0或1。m代表训练集的训练样本个数,或m_train表示训练集,m_test表示测试集的样本数。
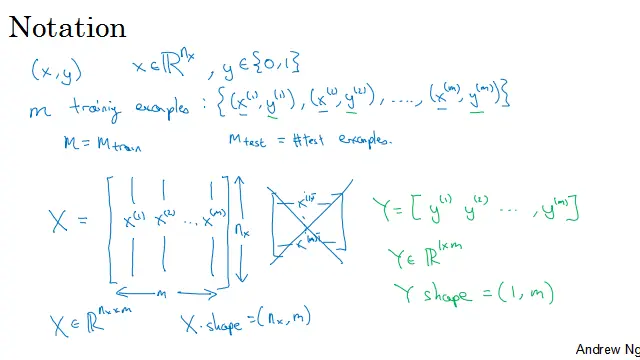
如上图所示,用一个矩阵(X)来表示训练集,它由训练集中的x1、x2这些组成,将其写成矩阵的列,每一列是一个特征向量x(如一张图片、一句话),一共m列(m个图片、m个文本)。这个矩阵的高度为nx,即特征向量的维度(一张图片的像素数*3、一句话的长度)
要注意的是,有时矩阵X的定义,将训练样本作为行向量堆叠,而不是这样的列向量堆叠。即将x1、x2、……、xm进行转置。但是构建神经网络时,用列向量堆叠的形式,会让构建过程简单许多。
则X是一个nx*m的矩阵,当用Python实现的时候,有一条命令X.shape用来输出矩阵的维度,即(nx,m),表示X是一个nx*m的矩阵。这就是如何将训练样本,即输入x用矩阵表示。输出标签y呢?为了方便,构建一个神经网络,将y标签也放在列中,即y1、y2、……、、ym,这里的Y是一个1*m矩阵。同样的在Python中,Y.shape等于(1,m),表示这是一个1*m矩阵。
好的惯例符号,能够将不同训练样本的数据联系起来。将不同的训练样本数据取出来放在不同的列上。




