1.算法描述
在一些应用领域数据可以自然而然地表示成图结构,包括 蛋白质组学,图像分析,场景描述 ,软件工程,和自然语言处理。最简单的图结构包括单一节点和序列。但在一些应用中,信息组织在一些更为复杂的图结构中,比如树,非循环图或循环图中,数据关系开采 已经成为归纳逻辑设计工作室许多研究的主题,并且近年来这项研究主题已经深化到诸多不同领域,当然这和数理统计和神经网络的相关概念在这些领域的应用密不可分。
在机器学习中,结构化数据和通过对样本(有监督或无监督的)学习的目标有关,通过一个将图像G映射到实数矢量的函数。 在这篇论文中,图像领域的应用大致可以区分为两大类:聚焦线和聚焦节点的应用。在聚焦连线的应用中,该函数不依赖节点并将一个分类或回归量运用于图结构数据集。比如,一个化合物可以用图建立模型,其中那些节点表示原子,边表示将原子联系起来的化学键[见图.1(a)]。这种映射可以用于估计该化合物造成某种疾病的概率。在图.1(b),一张图片由区域邻接的图表示,其中节点表示强度上具有同性质的区域,弧线表示他们的邻接关系。在这个例子中,被用于对图片归类,根据图中城堡,车,人等内容。
在聚焦节点的应用中,依赖节点,以此其分类或统计回归依赖于每个节点的固有关系。目标侦查是这类应用的一个例子。找出一张图片是否包含了被搜寻目标,并且如果有,标示其位置。这个问题可以由一个函数解决,它能将邻接区域图的节点分类,根据对应区域是否符合目标。比如,图1.(b)的输出可能是1标示契合城堡的黑色节点,并且其他的用0表示。另一个例子来自网络。网站可以由图表示,节点表示网页,边表示之间的超链接[图.1©]。网站连通性可以被利用,通过网页内容,来达到一些目的,比如将网页划分为一组主题。

传统机器学习的应用通过使用一个预处理阶段处理图结构数据,这一阶段将图结构信息映射为一个简单的表述,比如实数向量。换句话说,预处理步骤将图结构“压扁”成实数向量,之后通过基于列表的数据处理技术处理预加工数据。然而,重要信息,比如每个节点的拓扑从属信息可能会在预处理阶段损失并最终结果会以不可预测的方法取决于预处理算法的细节。更近年来,有各种方法,尝试保留数据的图结构属性。这种思路想将存在潜在图结构的数据编码,通过使用图中节点的拓扑关系,借此将图结构信息包含在数据处理阶段。
GNNs是基于信息扩散机理。一个图被处理为一系列单元,每个相当于图的节点,他们根据图的连通性联结着。这些单元刷新它们的状态并交换信息直到它们达到稳定平衡。之后基于单元的状态,GNN的输出可以在节点层间计算出。扩散机理的限制使得一个独特的稳定平衡总是存在。这种认识机制已被用在蜂窝神经网络及Hopfield神经网络。在这些神经网络模型中,连通性根据预定义的图描述,网络的连接自然属性上是循环周期性的,神经元的状态通过达到一个平衡点来计算。GNNs有别于蜂窝神经网络及Hopfield神经网络在于它们可以用在处理更广泛类型的图,如无向图,并且它们采用更综合的扩散机制。
GNN神经网络,整个训练的算法流程我们按如下的步骤进行:



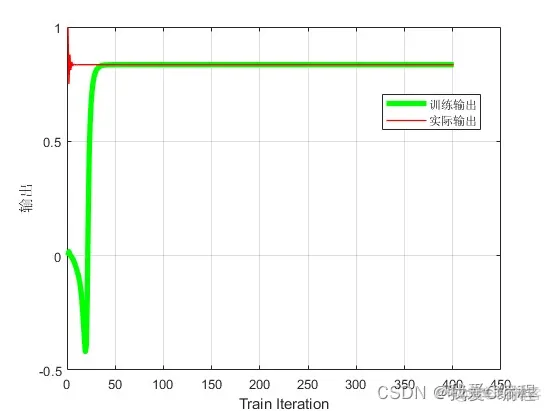
2.仿真效果预览
matlab2022a仿真结果如下:





3.MATLAB核心程序
Index = 0;
for nn = 1:length(Nodes)
Nodes(nn)
tic;
Index = Index + 1;
%初始参数
%学习率
Learn_rate = 0.2;
%惯性
lemda = 0.01;
%网络结构参数
Num_I = 40;
Num_Hide = 120;
Num_O = 1;
%训练次数
Train_Time = 40;
%初始化神经元输入信号
dw = cell(1,Num_I);
delta = [zeros(1,Num_Hide)];
x = [zeros(1,Num_I)];
Yout = 0;
du = 0;
Yout_Delay = zeros(1,Num_I);
l = zeros(1,Num_I);
%隐藏层神经元的输出
Oh = zeros(Num_Hide,1);
I = Oh;
Oh_delay = Oh;
%初始化突触权值参数
Net = func_initialize(Num_I,Num_Hide,Num_O);
%forward
x = func_forward(Net,l);
k = 0;
while(k <= Train_Time | k <= Nodes(nn))
k = k + 1;
%模拟训练数据和训练目标
P(k) = 1;
Yout(k) = (0.5*Yout_Delay(1)+P(k))/(1 + Yout_Delay(1)^2);
[Yout_Est(k),I,Oh] = func_backward(x,Net,Oh_delay,Num_Hide);
Err(k) = Yout(k) - Yout_Est(k);
%Jacobian
Jacobian_out(k) = func_Jacobian(Net,delta,Num_Hide);
%更新网络系数w
[Net,dw,delta] = func_w_update(x,I,Net,dw,Err(k),Learn_rate,lemda,Oh,Oh_delay,Num_I,Num_Hide);
%FORWARD
l = [Err(k),Yout(k),Yout_Delay(1:end-2)];
x = func_forward(Net,l);
%Delay;
Yout_Delay(1) = Yout(k);
for idx = 2:Num_I
Yout_Delay(idx)=Yout_Delay(idx-1);
end
Net.wd2{1} = Net.wd1{1};
Net.wd1{1} = Net.w{1};
Net.wd2{3} = Net.wd1{3};
Net.wd1{3} = Net.w{3};
Net.wd2{2} = Net.wd1{2};
Net.wd1{2} = Net.w{2};
end
toc;
time(Index) = toc;
end
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删