计算机层析成像技术(CT)是近十几年发展起来的一种新的非接触无损检测技术,它具有检测精度高、重建图像无影像重叠、空间分辨率和密度分辨率高、可以直接进行数字化处理等优点,现已被广泛应用于航空、航天、机械、公安、海关、医疗等诸多领域。滤波反投影算法是目前比较常用的CT图像重建算法,它速度快,图像质量好。但在二维平面上,Radon变换不具有局部性。于是,寻找一种既能减少辐射剂量,又能重建感兴趣区域的局部图像重建算法,引起了人们的极大兴趣,这就是所说的局部CT。最后利用MATLAB对滤波反投影算,多尺度全局重建和多尺度局部重建进行了仿真,从而验证算的正确性。

其中O(x,y)代表原始图像,R(x,y)代表重建图像。当然孤立地去看相对误差并不是一个好的衡量标准,它必须同人们的视觉评估结合起来进行考虑。
用S-L头模型进行计算机仿真研究的主要好处之一是可以获得该模型投影数据的解析表达式。一个中心位置在原点且未经旋转的椭圆,其长轴与X轴重合,短轴与Y轴重合。假设椭圆内的密度为r、椭圆外密度为零,则该椭圆图像可用以下方程表示:
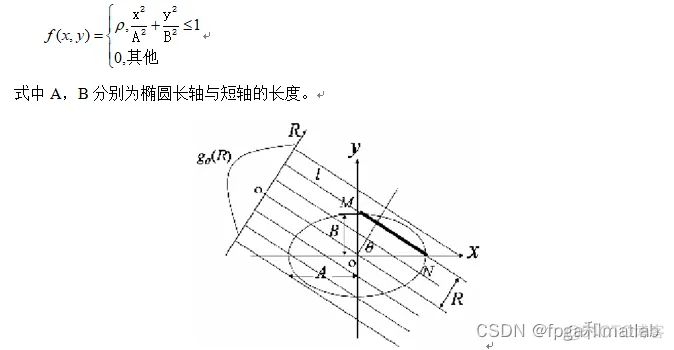
在研究从投影重建图像的算法时,为了比较客观的评价各种重建算法的有效性,人们常选用公认的Sheep-Logan 头模型作为研究对象。该模型由10个位置、大小、方向、密度各异的椭圆组成,象征一个脑断层图像。图3-2是S-L头模型的灰度显示图像。

clc;clear;close all;I=phantom(256); %生产头部模型图figure(1);imshow(I); %显示图像IMG=double(I);
%双精度显示%=====step1================================THETA=0:179;PR=touyin(IMG,THETA) %进行投影figure(2);
imshow(PR,[]);%=====step2================================filtPR=lvbo(PR);%进行滤波figure(3);imshow(filtPR,[]);
%=====step3================================BPI=fantouyin(filtPR,THETA);%反投影figure(4)imshow(BPI,[]);
imwrite(BPI,'BPI.bmp'); 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.
function filtPR=lvbo(PR);n = size(PR,1);sideSize = n;a = 1;[Length, Count] = size(PR);
w = [-pi:(2*pi)/Length:pi-(2*pi)/Length]; rn1 = abs(2/a*sin(a.*w./2));rn2 = sin(a.*w./2);
rd = (a*w)./2;r = rn1*(rn2/rd)^2; f = fftshift(r);for i = 1:Count IMG = fft(PR(:,i));
fimg = IMG.*f'; g(:,i) = ifft(fimg);endfiltPR= real(g); 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18
.19.20.21.22.
clc;clear;close all;I=phantom(256); %生产头部模型图figure(1);imshow(I); %显示图像IMG=double(I);
%双精度显示[cod_a,cod_h,cod_v,cod_d,map]=wtest(IMG);%一层小波变换figure(2);subplot(221)imshow(cod_a,map);
subplot(222)imshow(cod_h,map);subplot(223)imshow(cod_v,map);subplot(224)imshow(cod_d,map);
Z1=idwt2(cod_a,cod_h,cod_v,cod_d,'db1');figure(3);imshow(Z1,map);for i=1:256 for j=1:256
error(i,j)=(I(i,j)-Z1(i,j))^2/I(i,j)^2; endendfor i=1:256 for j=1:256 if I(i,j)==0
error(i,j)=255; end endendfor i=1:256 for j=1:256 if error(i,j)>255;
error(i,j)=255; end endendfigure(4);imshow(error,map); 1.2.3.4.5.6.7.8.9.10.11.12.13.14.
15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.
51.52.53.54.55.56.57.58.59.60.61.62.63.64.基于shepp-Logan模型的多尺度局部重建的MATLAB仿真与分析
其仿真图像为:

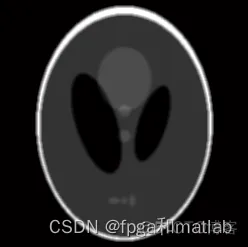
图1 原始仿真图(左)和局部数据仿真图(右)
其小波系数仿真如下所示:
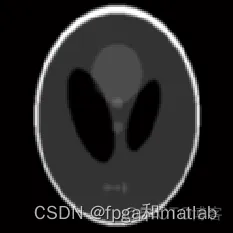
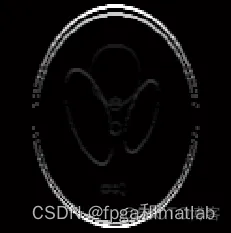


图2 小波系数
最后由局部数据重建的图像如下所示:
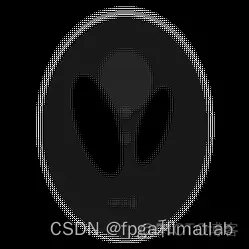
图3 局部数据重建效果
基于shepp-Logan模型的多尺度全局重建的MATLAB仿真与分析
我们首先用一层小波变换得到分解后的小波系数。仿真结果如下所示:




图4 小波系数
然后通过二维反小波变化,可以得到如下仿真结果:

图5 小波重建结果
A09-02
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删