最近在学习师兄师姐的论文,看到海梅师姐的论文,对SAMP算法有了一些兴趣,遂将代码进行调试更改,尝试更深入的学习压缩感知重构之稀疏度自适应匹配追踪算法。
首先对压缩感知的基本理论作一个说明:


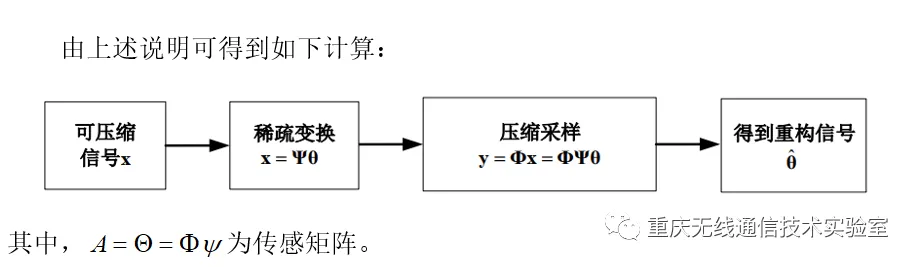
SAMP算法不需要知道信号稀疏度K,通过设置步长和合适的停止条件来进行稀疏度的估计和支撑集的填充。SAMP算法思想主要源于SP算法,SAMP算法是在SP算法基础上设置了固定步长S,在稀疏度未知的前提下,逐段估计原始信号稀疏度K,具有较好的重构效果。但是SAMP自适应的过程中对步长要求比较苛刻,S的取值一旦固定,在方法执行过程中无法更改。当S取值较大时,SAMP算法的迭代次数较少,但稀疏度估计值与实际值相差较大,重构效果较差。当S取值较小时,虽然信号的稀疏度估计值与实际值误差较小,但是降低了算法的效率。
SAMP实现算法如下:
1. function [ theta ] = CS_SAMP( y,A,S ) %这里的y输入是观测向量
2. [y_rows,y_columns] = size(y);
3. if y_rows<y_columns
4. y = y';
5. end
6. [M,N] = size(A); % 传感矩阵A为M*N矩阵
7. theta = zeros(N,1); % 用来存储恢复的theta(列向量)
8. Pos_theta = []; % 用来迭代过程中存储A被选择的列序号
9. r_n = y; % 初始化残差(residual)为y
10. L = S; % 初始化步长(Size of the finalist in the first stage)
11. IterMax = M;
12. for ii=1:IterMax % 最多迭代M次
13. % 初步测试
14. product = A'*r_n; % 传感矩阵A各列与残差的内积
15. [val,pos]=sort(abs(product),'descend');% 降序排列
16. % 详细说明:这里得到val是降序排列之后的向量,pos则是排序之后val向量中每个元素原先的索引值
17. Sk = pos(1:L); % 选出最大的L个,也就是得到最初的索引值
18. % Ck这里的操作是将两个数组合并,去掉重复数据,并且升序排序,也就是支撑集
19. Ck = union(Pos_theta,Sk);
20. % 最后测试
21. if length(Ck)<=M % 如果支撑集小于观测向量的长度
22. At = A(:,Ck); % 将A的这几列组成矩阵At
23. else
24. theta_ls=0;
25. break;
26. end
27. % y=At*theta,以下求theta的最小二乘解(Least Square)
28. theta_ls = (At'*At)^(-1)*At'*y; % 最小二乘解
29. [val,pos]=sort(abs(theta_ls),'descend'); % 降序排列
30. F = Ck(pos(1:L));
31. % 计算残差
32. % A(:,F)*theta_ls是y在A(:,F)列空间上的正交投影
33. theta_ls = (A(:,F)'*A(:,F))^(-1)*A(:,F)'*y;
34. r_new = y - A(:,F)*theta_ls; % 更新残差r
35.
36. if norm(r_new)<1e-6 % 满足停止的阈值 残差的范数<1e-6
37. Pos_theta = F;
38. break; % 满足阈值条件就停止迭代
39.
40. elseif norm(r_new)>=norm(r_n)
41. % 这里做了一个切换,意思是说,如果新的残差的范数比之前的范数大,说明
42. % 重构不够精准,差距过大.
43. L = L + S;
44. if ii == IterMax % 最后一次循环
45. Pos_theta = F; % 更新Pos_theta以与theta_ls匹配,防止报错
46. end
47. %ii = ii - 1;%迭代次数不更新
48. else
49. Pos_theta = F; % 更新Pos_theta以与theta_ls匹配,防止报错
50. r_n = r_new; % 更新残差
51. end
52. end
53. theta(Pos_theta)=theta_ls;%恢复出的theta
54. end
可以发现步长S在一定范围内时,其残差之间的变化是非常小的,说明在超过一定迭代次数之后,重构的精度几乎没有什么变化。我们试着改变一下信号x的长度,也就是增大数据量。详细的数据不在列出,发现增大信号x的长度到512,会直接导致残差的增大一倍,在步长为40时,残差增大到30左右,那整个重构就是失败的。另外,时间则随着步长的增大减小,是因为迭代次数的减小从上述整个测试的过程发现,在相应的信号长度下,也就是M值,步长和稀疏度会对整个重构精度有不小的影响。
1、更改稀疏度为5-50,其余保持不变,得到下表:
| 稀疏度K | 时间s | 残差 |
| 5 | 0.011483 | 2.2204e-15 |
| 10 | 0.024718 | 6.4422e-15 |
| 15 | 0.003003 | 1.3206e-14 |
| 20 | 0.008967 | 1.0616e-14 |
| 25 | 0.004132 | 1.5783e-14 |
| 30 | 0.003435 | 1.4340e-14 |
| 35 | 0.008961 | 2.2982e-14 |
| 40 | 0.004503 | 2.2043e-14 |
| 45 | 0.012251 | 2.4469e-14 |
| 50 | 0.034211 | 4.3466e-14 |
能够发现,稀疏度在15-30之间时,其重构的精度更好。所以在面对实际情况时,变换域的选择以及相对的稀疏度值非常重要。
在经过仿真分析之后,我们发现SAMP在不知道具体稀疏度值时依然能有一个非常好的表现,但是其固定步长对实际情况中算法的影响还是非常大的,在不同的稀疏度,不同信号长度下,其重构的精度和成功的概率会受到很大的影响,那么一个自适应步长的SAMP算法可能在面对这个问题时能够有更好的重构成功的概率。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删