齿轮动力学行为仿真分析

2K-H行星齿轮传动由于具有体积小、重量轻、速比大、效率高的特点,在民用、国防工业中都得到

了广泛的应用。近年来,国内外学者对行星齿轮传动的动态特性已经进行了大量研究[1～ 6]。但其中绝大多数研究者在进行建模和分析时不考虑间隙的影响,采用线性振动理论研究系统的动态特性[1～ 5]。即使考虑了间隙非线性因素,也仅用于讨论系统的动载问题,而未对系统的非线性动力学特性,如次谐响应、混沌与分岔等进行深入分析[6]。由于润滑、安装、加工以及磨损等原因,齿轮啮合不可避免地存在间隙,导致轮齿间在高速轻载下接触、脱离、再接触的重复冲击,从而引发强烈的振动、噪声及较大的动载荷,影响齿轮传动的寿命和可靠性。在实际齿轮传动系统中,引起灾难性事故的原因常常是系统的异常振动(非工频振动),这种动态行为是无法用线性振动理论解释的。因此,必须采用非线性振动理论,对系统的动力学行为进行研究。以2K-H行星齿轮系统为研究对象,考虑齿侧间隙,深入研究行星齿轮系统的非线性动态特性,不仅对于进一步探究行星齿轮系统的动态特性、降低行星齿轮减速器的振动与噪声具有重要的实用指导意义,而且可以为设计

高质量的行星齿轮系统提供有益的理论根据和有效手段。

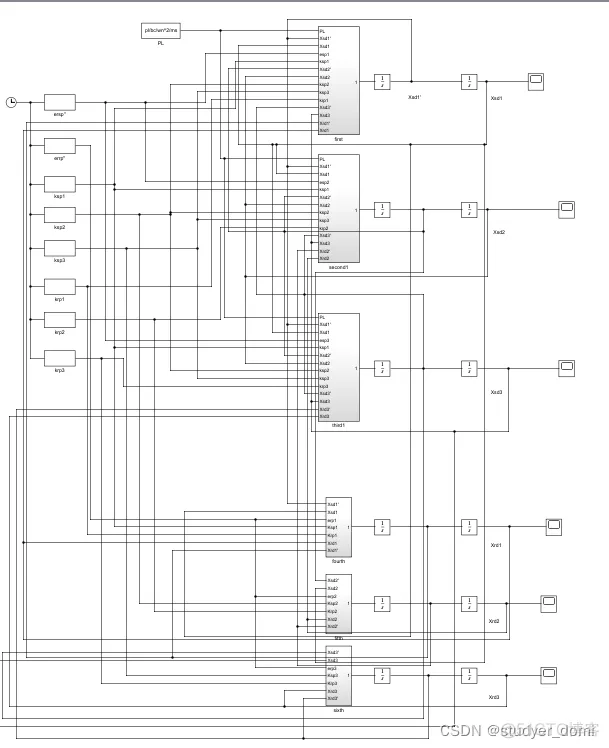
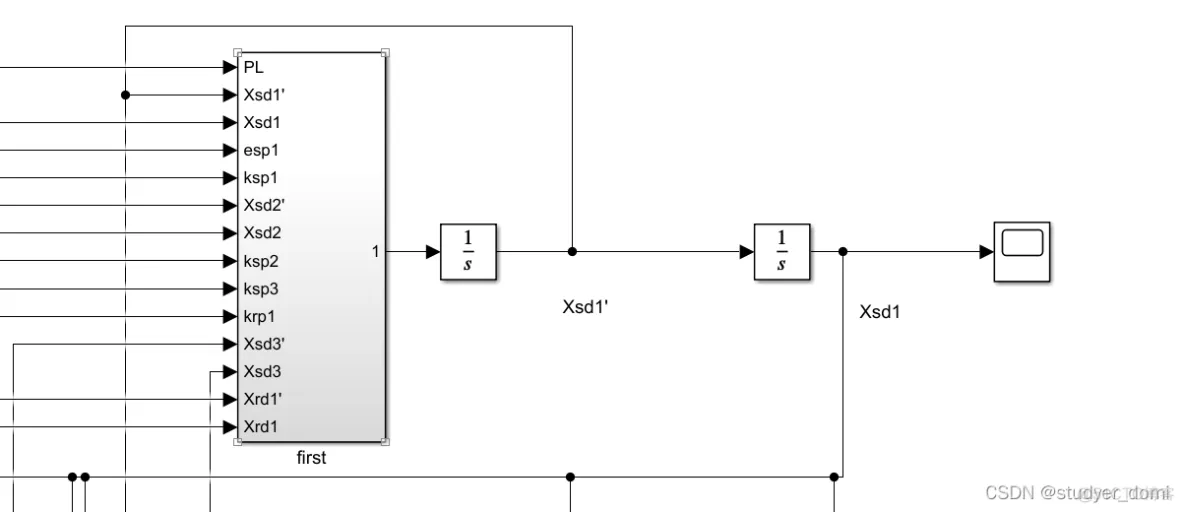
1　 2K-H行星传动的非线性动力学模型2K-H行星齿轮传动如图1所示。系统由太阳轮、N个行星轮、行星架和齿圈构成。　　建模时采用集中质量模型。假定齿轮均为直齿圆柱齿轮,且各行星轮具有相同的物理和几何参数,不计齿轮啮合时摩擦力的影响。建立的2K-H行星帀車

参数：

Wn=0.7297 ;

T=9549*(pw)/n ;

Pw=200 ;

Rbs=38.3 ;( Rbs就是Rb1)

pL= T/ Rbs ;

RP（Rb2）=6;

Rbr=49.4;

Tp=7T/72;

Pdi= Tp/RP;

MS=219.72

MP=67.2;

W=123.4568

Tm=0.0081;

KSp1=27.4182+13.2788*sin(w*t);(i=1-2)

Kspi=ks1(t-13*i* Tm);

krp1=16.4182+7.28*sin(775.71*t);

Krpi=krp1(t-13*i* Tm);

=0.03;

ers=20e-6;

err=20e-6;

ersp= ers+0.2*ers*cos(w*t);

errp= err+0.2*ers*cos(w*t);(注意方程是误差的二阶导数，请变换)

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删