FPGA探索（61）时间换空间的时空策略

逻辑合并

逻辑合并，是用时间换空间时，最常用、也是最简捷有效的一种做法。它的基本思路是将寄存器从组合逻辑的路径上抽掉，从而让它前后的组合逻辑融合为一个较复杂的组合逻辑，进而在增加了组合逻辑的时间延迟情况下，节省了一些寄存器资源。当然了，前提是这样做不会改变时序电路的功能。举例说明如下：
下述示例代码实现的是四个数A~D的求和功能：

-- VHDL example	
	signal tmp1, tmp2 : std_logic_vector(7 downto 0);
	process(clk)
	begin
		if clk'event and clk = '1' then
			tmp1 <= A + B;
			tmp2 <= C + D;
			SUM <= tmp1 + tmp2;
		end if;
	end process;
	
	// Verilog example	
	reg [7:0] tmp1, tmp2;	 
	always@(posedge clk)
	begin
		tmp1 <= A + B;
		tmp2 <= C + D;
		SUM <= tmp1 + tmp2;
	End

对于上述代码，编译器通常会将它翻译成如下电路：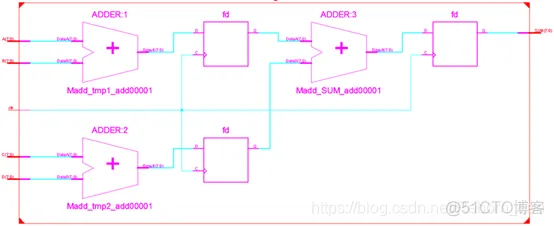

从上图可以清晰的看到，该电路的时间性能是比较好的，因为从输入端口到第1级寄存器之间，以及从第1级寄存器到第2级寄存器之间，组合逻辑的延迟都仅为1级加法器，不过它却消耗了3组寄存器（每组的数量跟输入端口的位宽有关）资源。若现在对求和电路的时间需求并不高，但希望其能变得更加节省资源一些，便可以应用逻辑合并的思路，对其进行以时间换空间的变换。修改后的代码如下所示：

-- VHDL example	
	process(clk)
	begin
		if clk'event and clk = '1' then
			SUM <= (A + B) + (C + D);
		end if;
	end process;
	
	// Verilog example	
	always@(posedge clk)
	begin
		SUM <= (A + B) + (C + D);
	end

而编译器所给出的对应电路通常如下：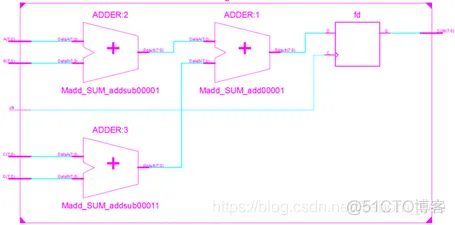

对比代码修改前，编译器所给出的电路结果，可以明显看出，组合逻辑所占用的资源前后等价，但修改后的求和电路仅消耗了1组寄存器资源，比修改前的电路减少了2组之多，因此提升了该求和电路在空间方面的余量。不过从输入端口到寄存器之间却经历了2级加法器，因此该求和电路在时间方面的性能也大大下降。这便是逻辑合并所带来的以时间换空间的结果。

模块复用之提速复用原理

提速复用是模块复用的第二类方式，也是一种比较高级的以时间换空间的方法。
提速复用也是针对处理当FPGA设计中需要用到两个以上功能一样的模块时的空域优化需求，但比较特殊的是，此时每个模块所占用的资源都已经被充分利用，并且各个模块的调用又都是同时的，因此无法使用【时空变换之空域优化】章节中介绍的资源合并与分时复用的方法来提升空间方面的性能。
提速复用的原理是通过提高模块的工作时钟速率，来提高模块的瞬时处理能力，从而可以人为的将原本需要被同时调用的模块在微观或宏观上设计成串行调用的方式，这样一来，便可采用分时复用的方法来进行空域优化。由于提升模块的工作时钟，会极大的减小模块在时域方面的余量，因此提速复用是典型的以时间换空间的做法，并且如果提速过多，将会造成时序约束不满足的情况，所以在实际的运用中需要拿捏准确。由此也可以看出，以时间换空间的前提条件是时间方面具有足够的余量。
按照提速后，具体的复用方式，又可将提速复用划分为简单提速复用、复杂提速复用和缓存提速复用三种。其中，简单提速复用和复杂提速复用都是利用模块提速后微观的空闲时隙完成复用，而缓存提速复用则是利用模块提速后宏观的空闲时隙完成复用，下面各个小节将对它们分别进行详细的介绍。

简单提速复用

简单提速复用是指提速后的模块具有可以直接分时复用的特性，即可以采用类似【模块复用之时分复用】小节中介绍的方法来完成资源方面的节省。通常来说，可以采用简单复用的模块，主要是纯组合逻辑的模块，因为只有对于这样的模块，提速后在微观上才具有直接的串行特性。
例如，逻辑块A需要持续使用一个乘法器进行乘法运算，由于A中的数据率为10MHz，因此该乘法器只要在100ns的时间内完成运算就可以保证逻辑A行为的正确性。若逻辑块B、C也需要持续使用一个一摸一样的乘法器，并且也以10MHz的频率进行乘法运算，那么最初的方案通常都是为每一个模块单独配备一个乘法器，所以总乘法器消耗量为3个。假设该乘法器只需要在20ns内就可以给出正确的乘法结果，那么对于每一个乘法器来说，时间方面还有80ns的余量。此时如果将它们的工作时钟频率提高到3倍，即达到30MHz，时钟周期变为33.3ns，那么每个乘法器仍然具有13.3ns的时间余量，可以给出正确结果。但是此时由于逻辑块A~C中的数据率仍然是10MHz，因此每个乘法器就会出现微观上的时间冗余，即每3个连续的时钟周期中，仅有1个是乘法器工作状态，剩下2个都是其空闲状态。对于每一个逻辑块来说，3个连续时钟周期中，到底哪一个对应乘法器的工作状态都是无所谓的，因为只要在100ns内给出乘法结果，原有逻辑块的功能行为就不会改变。因此，如果我们人为的安排逻辑块A在第1个时钟周期使用其乘法器，逻辑块B在第2个时钟周期使用其乘法器，逻辑块C在第3个时钟周期使用其乘法器，那么接下来，仅需要采用【时空变换之空域优化】章节中介绍的模块分时复用的方法，就可以将乘法器的个数从3个降至1个，达到以时间换空间的目的。
在上例中，倘若每个乘法器需要90ns才能得出正确的乘法结果，那么提速复用的方法将不能使用，因为此时该乘法器在时间方面已经没有足够的余量。
在现实中，简单提速复用方法的一个最典型的应用当数数据通信时的“并串+串并转换”了。“并串+串并转换”的方法，将原本需要用多根并行的数据线来实现的低速率数据通信方式转化为仅需要1根串行数据线的高速率数据通信方式。这虽然减少了通信系统的时间余量，但是却极大节省了通信线缆等硬件资源。具体的“并串+串并转换”方式请大家回顾【本篇->编程思路->关于外界接口的编程思路->按数据位宽分类】章节中的介绍。

复杂提速复用

虽然说提速后的模块，在时间方面都会出现一定的余量，但是由于模块内部算法结构的不同，有些情况下无法直接通过简单套用时分复用的方法来达到节省资源的目的。通常来说，时序逻辑模块的复用为复杂提速复用，因为提速后的模块必须经过较大修改才能保持原有的逻辑行为。因此，我们将那些提速后，还需要对模块内部结构进行修改方可进行模块复用的情况，统称为为复杂提速复用。而复杂提速复用又跟模块内部的算法结构有关，因此不同情况下的具体表现形式也可能往往大相径庭，下面就以数字信号处理中最常用到的FIR滤波器为例，来介绍一下其复杂提速复用的表现形式，并以此为基础，推理出复杂提速复用的一般处理方案。

一个简单的FIR滤波器

让我们以一个简单的4阶FIR滤波器作为研究对象，滤波器的公式为：
y[n] = h[0]x[n] + h[1]x[n-1] + h[2]x[n-2] + h[3]x[n-3];
参考数字信号处理的相关知识，可知其对应的滤波器结构框图如下：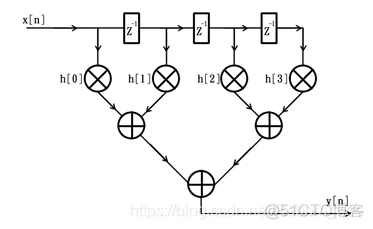

FIR滤波器的转置结构

上述FIR滤波器的结构框图并不适合在FPGA中实现，因为随着阶数的增加，从输入x[n]到输出y[n]之间的组合逻辑延迟也会不断增大（即使采用了二叉树的组织结构，当阶数超过几十之后，加法器的级数也会增加到6级以上），而这会极大的限制滤波器的性能和应用场合，因此，通常情况下，我们在FPGA中采用的都是滤波器的转置结构。仍以上述4阶滤波器为例，其转置结构的原理框图如下：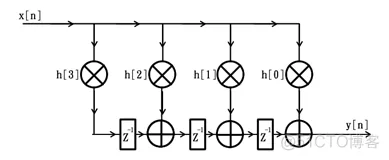

对比之前的滤波器结构框图，可以发现采用了转置型的滤波器结构框图后，无论滤波器的阶数为多少，从输入x[n]到输出y[n]之间的组合逻辑延迟始终为1个乘法器加一个加法器的延迟，因此FPGA中的滤波器均采用转置型的滤波器结构。当然了，为了保证滤波器的输出正确性，转置结构中的滤波器系数h[0]~h[3]的分布与初始结构中的滤波器系数排列恰恰相反。

多路FIR滤波需求初步分析

现在，若有3路连续的数字信号需要同时被上述4阶FIR滤波器处理，那么初步的方案一般是为每一路数字信号单独配备一个FIR滤波器，方案原理框图如下：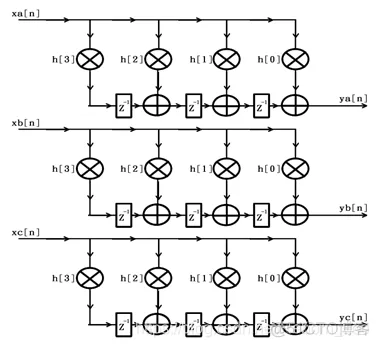

通过上图可见，该方案同时对3路数字信号进行FIR滤波处理，需要消耗3倍于对单路数字信号进行FIR滤波处理时的资源。

提速后的问题分析

FIR滤波器中需要用到乘法运算，而且现实情况中，为了达到比较好的滤波效果，FIR滤波器的阶数一般都不会太小，有时候甚至在一、两百阶左右，因此其对FPGA资源的消耗是比较大的。尤其是当我们同时连续采集多路数字信号时，如果每路信号都需要做同样的滤波处理，当采用上一小节中的方案时，同时例化多个同样的FIR滤波器对FPGA资源的侵蚀会是一件非常可怕的事情。而且，这种同时处理多路数字信号的需求是非常普遍的，因此，我们必须找出更加合适的方案，来让具有N个同样滤波器的FPGA设计具有明显小于N的资源膨胀比率。
由于资源方面使用充分，时间方面也没有互斥关系，因此资源合并或分时复用都不可能，现在唯有尝试一下提速复用的方法。可是与简单提速复用的情况不同，滤波器属于时序逻辑，此刻的输出不光取决于此刻的输入，还和前几个输入有关，因此，就算乘法器和加法器的时间性能允许我们对其提速3倍工作，但由于输入序列是按照原始速率进行更新的，所以上述FIR滤波器将不能给出正确的结果。那么，为了将提速复用进行到底，我们必须对FIR滤波器的结构进行修改，以使其在提速后，不光能在微观上呈现出不同时工作的特性，并且仍能得到正确的输出结果。

FIR滤波器的复用方案

以下便是典型的FIR滤波器复用方案框图，注意，该框图工作的时钟频率是原来的3倍：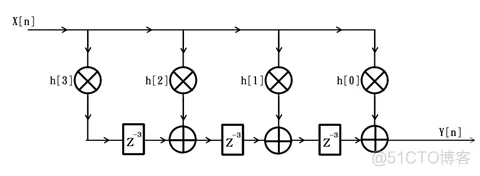

通过仔细观察可以发现，复用后的滤波器结构框图中，除了延迟单元由Z^{(-1)全部变为了Z}(-3)以外，其它部分的结构都没有变化。此时，如果我们令输入X[n]为：
xa[0]、xb[0]、xc[0]、xa[1]、xb[1]、xc[1]、xa[2]、xb[2]、xc[2]、xa[3]、xb[3]、xc[3]……
那么输出Y[n]就应该对应为：
ya[0]、yb[0]、yc[0]、ya[1]、yb[1]、yc[1]、ya[2]、yb[2]、yc[2]、ya[3]、yb[3]、yc[3]……
若FIR滤波器内部的寄存器初始值均为0，则，逐步分析滤波器内部的情况如下：
为了简便起见，令该FIR滤波器的所有系数均为1，那么第1个时钟周期过后，滤波器内部情况如下图所示：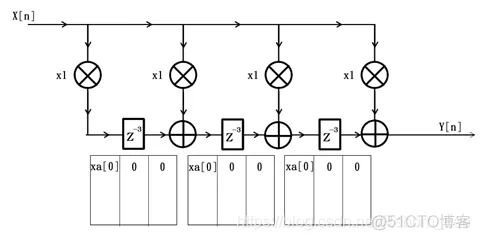

3个时钟周期过后，滤波器内部情况如下图所示：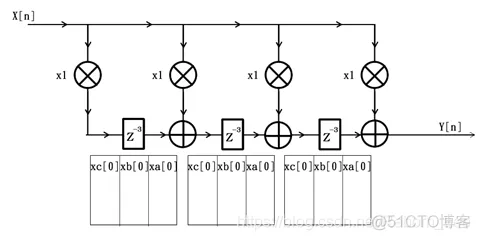

6个时钟周期过后，滤波器内部情况如下图所示：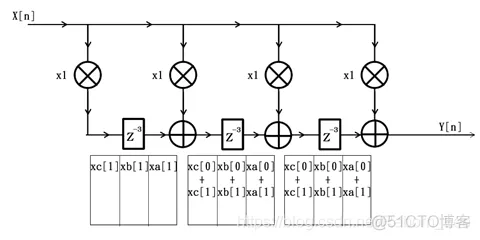

9个时钟周期过后，滤波器内部情况如下图所示：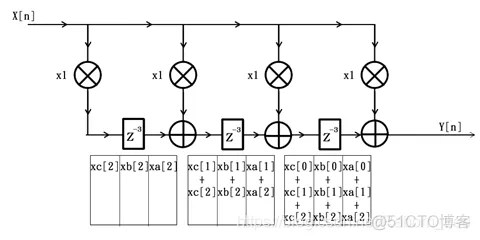

那么，第10个时钟周期后，滤波器的输出为
Y[10] = xa[0] + xa[1] + xa[2] + xa[3] = ya[3];
第11个时钟周期后，滤波器的输出为
Y[11] = xb[0] + xb[1] + xb[2] + xb[3] = yb[3];
第12个时钟周期后，滤波器的输出为
Y[12] = xc[0] + xc[1] + xc[2] + xc[3] = yc[3];
同时，滤波器内部情况如下图所示：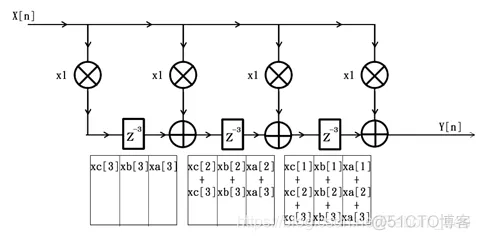

如此往复，该滤波器的输出序列Y[n]其实就对应为
、、、、、、、、、ya[3]、yb[3]、yc[3]、ya[4]、yb[4]、yc[4]、ya[5]、yb[5]、yc[5]、……
注意，前9个输出没有意义，因为我们无法得到负索引的X[n]，所以用表示，不过这9个输出等效于负索引X[n]全为0的情况。
综上所述，3路数字信号处理所采用的滤波器复用方案相比于单路数字信号处理方案，寄存器资源膨胀了3倍，但乘法器、加法器等资源没有任何一点增加，因此整体资源膨胀率远小于3倍，为系统节省了相当的空间余量，这便是复杂提速复用对于时间换空间的贡献。

FIR滤波器的其它优化

这里需要明确一点，那就是FIR滤波器在具体使用时，其所能优化的地方并不限于上述转置结构和复用结构的讨论。例如：
利用其系数的固定性，可以设计出更加简洁的乘法器；利用其系数的对称性，可以将乘法器的数量再减少一半；利用系数的重复性，可以进一步减少乘法器个数；利用系数等于0的情况，又可进一步减少乘法器的数量……
因此，实际在FPGA中实现的FIR滤波器，应该是结合了上述所有优化后的结果，并且如果利用【时空变换之时域优化->分布调整】小节中的方法，将乘法运算均匀分布到滤波器复用结构中的各组移位寄存器内部，将能得到进一步提升FIR滤波器的性能。

复杂提速复用的一般形式

我们可以从FIR滤波器的复用方案中得到启发，猜测出，也许时序逻辑的复用仅需要对模块提速后，再将其内部每一个寄存器替换成深度为N（N为复用的个数）的移位寄存器阵列即可。事实上，复杂提速复用的一般形式还真是如此！证明如下：
通过【本篇->编程思路->状态机，FPGA的灵魂】章节的学习，我们了解到时序逻辑就是状态机，因此，任何时序逻辑都可以表示成Moore、Mealy或Mix型状态机的结构 。若一个时序逻辑可以表示为Moore 1型状态机，那么其对应的逻辑结构框图如下：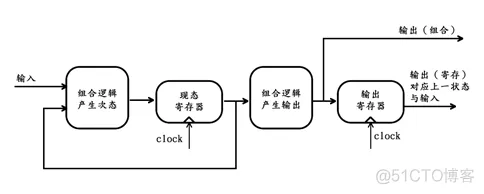

假设FPGA设计中需要同时用到2个这样的模块，那么，按照我们之前的猜想，可得该模块的提速复用方案为：将其内部每一个寄存器替换成深度为2的移位寄存器阵列。由于状态机结构中只存在两个寄存器——状态寄存器和输出寄存器，因此分别对它们进行替换后，可得复用方案如下图所示：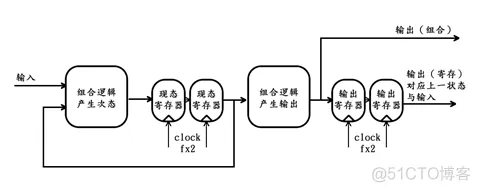

上图中，如果我们令输入X[n]为：
xa[0]、xb[0]、xa[1]、xb[1]、xa[2]、xb[2]、xa[3]、xb[3]、……
那么，我们期望——
系统的组合输出为：
yca[0]、ycb[0]、yca[1]、ycb[1]、yca[2]、ycb[2]、yca[3]、ycb[3]、……
系统的寄存输出为：
yra[0]、yrb[0]、yra[1]、yrb[1]、yra[2]、yrb[2]、yra[3]、yrb[3]、……
系统的状态输出为：
sa[0]、sb[0]、sa[1]、sb[1]、sa[2]、sb[2]、sa[3]、sb[3]、……
现证明如下：
初始或系统复位时，令状态移位寄存器阵列中的寄存器全部为该状态机的初始状态（即sa[0] = sb[0] = 初态），令输出移位寄存器阵列中的寄存器全部为0（输出寄存器的初值其实无所谓，因为有意义的输出要在状态机运行后才会出现，因此yra[0] = yrb[0] =0）。
因此初始时，该状态机的内部情况如下：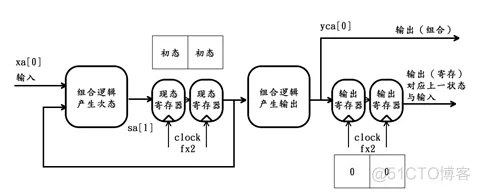

第1个时钟周期过后，该状态机的内部情况更新如下：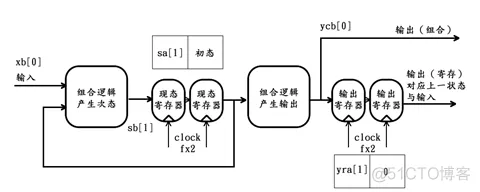

第2个时钟周期过后，该状态机的内部情况更新如下：

第3个时钟周期过后，该状态机的内部情况更新如下：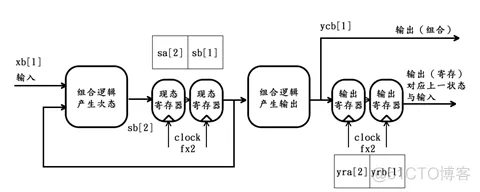

第4个时钟周期过后，该状态机的内部情况更新如下：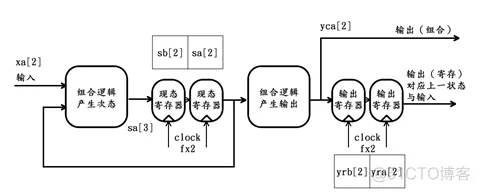

依此类推，可知该复杂提速复用方案的组合输出、寄存输出与状态输出均与之前的预期完全一致，并且若复用路数N大于2，也可类似得证。
同理可轻松证明其他Moore类型状态机以及Mealy、Mix类型状态机在直接套用最开始猜想出的方法后，也都可正确的完成提速复用，因此该猜想的正确性可证。
综上所述，针对时序逻辑模块的复杂提速复用是具有一般形式的（即通解），即，对于N路数据复用一个时序逻辑模块的情况，只需将该模块内部每一个寄存器都替换成深度为N的移位寄存器阵列即可！

缓存提速复用

简单提速复用和复杂提速复用，一个针对组合逻辑模块，一个针对时序逻辑模块，因此加起来就可以解决所有模块的提速复用问题，不过提速复用领域还存在一种方法，那就是缓存提速复用。
缓存提速复用的思路是，利用异步FIFO或者RAM，先将低速的输入数据缓存起来，当缓存中的数据达到一定数目后，再用一个比较高速的时钟一次性连续读出固定数目的数据并送给相应模块进行处理。由于原始输入数据的速率较低，因此，模块使用便会呈现出宏观的时隙，此时如果有多路数据需要被该模块处理，则可以利用该宏观时隙完成该模块的分时复用。例如，输入数据采样率为10MHz，缓存后以20MHz的时钟连续读出，若想每次都能从缓存中连续读出100个数据，那么必须每读100个数据就接着等待100个20MHz的时钟周期，因为只有这样才能保证平均读出数据速率与平均写入数据速率相等，缓存内部才能达到平衡。而这用作等待的100个20MHz的时钟周期，正是可被利用的宏观时隙。
缓存提速复用也是针对时序逻辑的一种提速复用方法，但它相比复杂提速复用具有一定的局限性。复杂提速复用适用于所有的时序逻辑，因为它有通解，但是缓存提速复用却只适用于那些可以将连续输入的数据分段进行处理的模块。例如，如果一个累加模块，每累加100个连续的输入数据后就给出一个阶段性的结果，然后再对接下来的100个数据进行累加并给出下一个阶段性的结果，依此类推，那么该模块就可以使用缓存提速复用的方法。反之，若该累加器持续累加输入数据直到系统停止工作前，那么它就无法套用缓存提速复用的方法。不过缓存提速复用实现起来更为容易，不需要更改原模块的结构，且在高频时钟的选择上更加灵活一些。
综上所述，复杂提速复用与缓存提速复用都是以时间换空间的好方法，不过相对于单个模块，复杂提速复用只会造成模块内部寄存器资源按照复用路数进行膨胀，而缓存提速复用不会造成原有模块的变化，但却需要对每路数据增加额外的缓存开销。因此对于那些即可以应用缓存提速复用，又可以应用复杂提速复用的时序逻辑模块，需要对比评估两种方法的资源开销，同时结合复用的人工工作量，选择资源与复杂度综合最优的那个作为最终的以时间换空间的方案。而对于那些不开放源代码的IP核，由于无法对其进行修改，在出现需要复用的情况时，就只有尝试使用缓存提速复用的方法了。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删