时间步长是除了单元平衡方程之外,显示动力学计算的最基础最重要理论公式
在LS-DYNA中关键字*CONTROL_TIMESTEP用于控制求解时间步长,时间步长为每一步有限元积分的长度。计算所需时间步长时,要检查所有的单元。最小时间步长计算公式
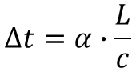
其中▲t是时间步长,α是时间步长缩放因子,L是单元特征长度,c是材料声速
α(时间步长缩放因子)对应DYNA中的关键字TSSFAC。在DYNA官方帮助文档中对α的解释为:计算稳定性的考虑,TSSFAC通常设置为0.90(默认值)或者更小。为了减少求解时间,我们希望使用更大的稳定的时间步长,但大于0.90的值通常会导致不稳定。
L是单元的特长长度,查阅DYNA帮助文档可知,各种单元特长长度的计算方法
壳单元
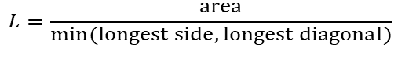
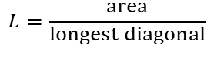
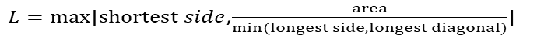
六面体单元
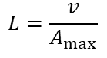
四面体单元
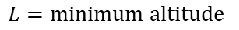
梁单元
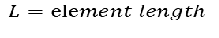
c为材料声速,查阅DYNA帮助文档可知,各种单元材料声速的计算方法
体单元
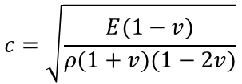
壳单元
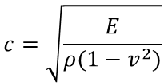
梁单元

其中E为弹性模量,p为密度,v为泊松比
通过以上公式,计算每一个单元的时间步长,例如:假设一个1mm*1mm四边形单元,密度为1,弹性模量为1,泊松比为0.3,时间步长缩放因子为0.9,该单元在DYNA显示动力学计算中的时间步长为
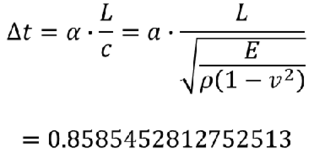
通过上述算例,,可知当某一模型完成网格建模、材料赋予后,模型的时间步长则是一个确定值(模型中最小网格尺寸单元的时间步长为模型的时间步长),然而在复杂模型中不可避免的会有小部分网格尺寸远小于模型目标网格尺寸,导致时间步长偏小,计算效率慢。

为了适当的增大时间步长,而不影响计算精度,从以下公式可知,可以适当增大c材料声速使时间步长增大,材料声速与弹性模量、泊松比、密度有关,改变弹性模量、泊松比会影响计算的应力应变结果,这是仿真不被允许的,因此,只能适当增大密度是时间步长增大。
当前行业惯例常说DNYA求解质量增量小于系统总质量的5%,对于一些刚入行的新人,在进行简单模型分析(如单轴拉伸样条仿真)仍特意调整质量增量5%,是不合理的,在此对质量增量进行说明
1.最理想求解,除去刚体、治具等非系统部件,系统质量增量为0%
2.次理想求解,除去刚体、治具等非系统部件,系统中每个零部件的质量增量小于5%
3.次次理想求解,除去刚体、治具等非系统部件,系统质量增量小于5%,关键零部件质量质量小于5%
4.次次次理想求解,刚体+治具+系统质量增量小于5%,此时容易造成计算不稳定,计算结果异常等问题(错误做法,不可取)
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删