不可压缩流动求解器基于应用于流体力学的现有有限元技术。它与固体力学求解器完全耦合。FSI 耦合分析,允许通过显式技术进行稳健的弱 FSI 耦合分析,或使用隐式进行强 FSI 耦合分析。除了能够处理自由 表面流动之外,使用保守的水平集界面跟踪技术,还可进行双相流分析功能。
还支持基本湍流模型。本求解器是 LS-DYNA 中第一个应用新的体网格划分器,它只需将流体域边界的高质量表面网格作为输入,然后由 程序自动生成体网格。另外,在随着不可压缩流的时间推进期间,求解器将自适应地重新网格化输入求解器 特点。
网格划分器的另一个重要特征是能够创建边界层网格。当在流体壁附近计算剪切应力时,这些各向异性边界层网格是模型求解关键。
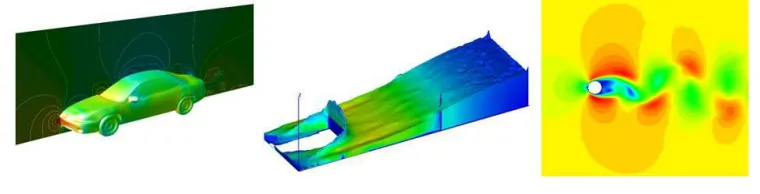
图 1 ICFD 汽车外流场、水流冲击大坝、圆柱扰流案列
ICFD 求解器使用自动体网格器划分流体域。 这极大地简化了前处理阶段,而且,提供高质量的表面网 格。 对于 FSI 流-固耦合分析,求解器使用 ALE 方法进行网格移动。 在 FSI 模拟导致大位移的情况下,求解器可以自动重新网格化以保证可接受的网格质量。

图 2 ICFD自动生成边界层及体网格
LS-Dyna为用户提供了几种工具用于细化局部体网格,以便更好地捕获网格敏感现象,例如湍流涡流或边界层分离和再附着。在几何体设置期间,网格划分器可以根据用户指定曲面,生成体积内的局部网格尺寸。如果没有使用内部网格来指定大小,则网格器将使用封闭体的表面大小进行线性插值。 为了能更好的模拟壁面效应,还可以添加一些各向异性的边界层网格。
另一种可能性是激活自适应网格细化特征。求解器将使用后验误差(a-posteriori error)估计器来计算由 用户界定的新网格大小,以满足最大感知全局误差,这将简化网格生成,同时提供准确的结果。
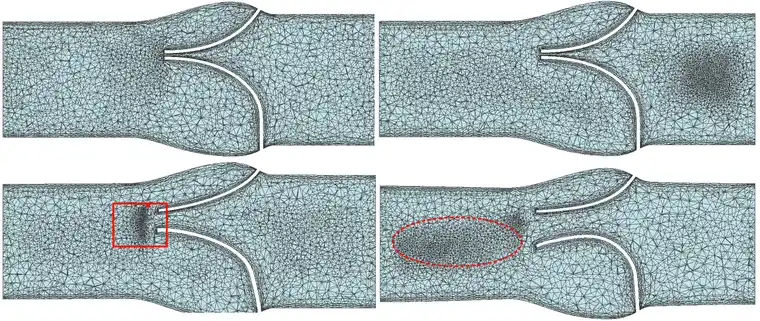
图 3 ICFD根据流场压力变化进行自适应网格重新剖分
LS-Dyna求解器的主要目标不仅是解决 Navier Stokes 方程,而且希望解决完全耦合的 FSI 流-固耦合问题,其中结构部分可以是 任何拉格朗日模型。因此,力学问题的设置与传统的 LS-DYNA 分析相同。
所有 FSI 流-固耦合边界都是拉格朗日变形,其结构允许精确地施加边界条件。结构力学的显式和隐式求解器 都可以被激活使用,从而可以实现弱 FSI 流-固耦合分析或强 FSI 流-固耦合分析。
FSI 分析有三种耦合方向:
双向耦合。载荷和位移通过 FSI 接口传递,解决了完整的非线性问题。
单向耦合。固体力学求解器将位移传递给流体求解器。
单向耦合。流体求解器将应力传递给固体力学求解器。

图 4 ICFD单向及双向流固耦合
在高雷诺数流动的情况下,对于正确地再现涡旋现象,依赖湍流模型的选择,边界层层流到湍流过渡和 其他湍流三维行为是至关重要的。以下几种湍流模型可用:
RANS 模型。 RANS 方程确定平均流量,但它们需要湍流模型来关闭它们。这些方程由不同的 RANS 模 型提供,假设流动有不同的假设。k-ε模型,这是 CFD 中使用最广泛的湍流模型之一。
LES 模型。随着计算机计算效率的提高,LES 模型已经成为一种流行的技术,以模拟湍流模型。这些模 型基于以下的假设:大涡旋包含流动的大部分动能并且取决于几何形状,而较小的涡旋被认为更通用且独 立于流动的几何形状。因此,LES 模型将对流动应用滤波器,直接解决大涡流,同时模拟较小的涡流。
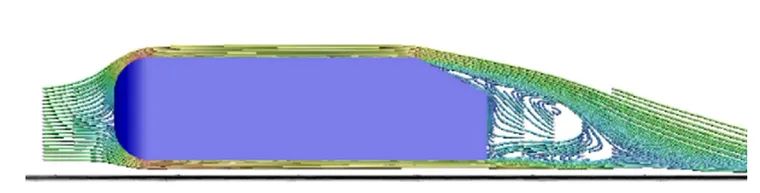
图 5 ICFD湍流模型
本血流动力学实例突出了 ICFD 求解器的最强 FSI 能力。由于压力差,心脏瓣膜小叶打开以允 许血液流动。然后,强烈的反压迫使它们再次关闭,血流量减少。本案列中对于瓣膜和血管壁均采用超弹性材料模型,难点在于当瓣膜在压力驱动下张开时,会带动流体网格产生较大的变形,通常为避免网格拉扯出现负体积,一般结合动网格,例如Comsol动网格。
但即便如此,仍会存在无法继续计算的问题,下图6展示为Comsol拉普拉斯动网格模型,并当网格质量较差时,打开网格重新划分,但是即使这样,当变形较大时,计算仍然停止了,上文介绍的ICFD网格自适应技术能够很好的弥补这点缺陷。

注:Comsol依然强大,只是本人找不到合适的方法,在此没有说明Comsol软件能力弱
图 6 Comsol动网格及网格重新划分心脏瓣膜模拟

图 7 心脏瓣膜网格自动剖分展示

图 8 心脏瓣膜仿真流场压力展示

图 9 心脏瓣膜打开模拟
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删