1. 模型介绍
本模拟主要研究单伞、三伞、四伞在重力场中负载重物下的展开情况,模型具体尺寸为(伞长,展开面积,伞绳长度),对于重物端采用实体建模,分为重物和托盘2部分组成,托盘与柔性伞绳采用共节点方式连接,初始状态预设轴向预紧力,模拟货物在重力状态下的拉紧状态。


图 1 伞衣及重物连接方式


图 2 伞衣与伞绳、伞绳与重物绳连接方式
伞衣雨伞绳尾端同样采用共节点方式连接,本模型中比较关注伞绳轴向受力及变形,可以认为伞绳仅受轴向力,因此可以简化为一维单元,采用离散梁单元来模拟伞绳以及重物绳,具体建模如图2。对于伞衣与伞绳之间的连接为一维梁单元和壳体单元的之间的接触,通常对于节点自由度不同的两个节点或者单元采用共节点的方式建立接触,但是需要注意的是建立完共节点接触后,自由度的个数由较低节点决定,本模拟中共节点处的自由度由梁单元决定。





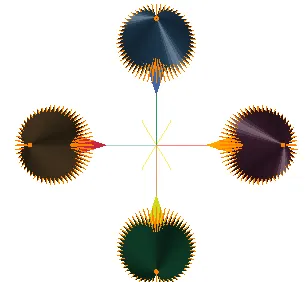
图 3 单伞衣、三伞绳、四伞衣工况
图3为三种伞衣组合工况,分别模拟三种工况下,伞衣的展开情况。降落伞是一个复杂的气动弹性体 ,具有敞开式织物可拉伸透气结构。一般把降落伞当成是由比较小的厚度而又有比较大的变形量的薄膜材料组成。由此,可将降落伞离散为一系列用阻尼弹簧连接的质点。本模拟中降落伞模型为事先折叠好的模型,当气流冲入伞衣时形成空腔,气流在伞衣内发生流固耦合,压力增大。伞衣质点在弹性力、阻尼力和气动力的共同作用下运动,使得伞衣逐渐张开。但实际降落伞在气体压力下的张开是个较为复杂的流固耦合过程,从数值模拟角度分析需要建立理想假设:
1)忽略质点的重力影响,充气过程是轴对称的;
2)各质点之间用伞绳、加强带和伞衣连接;
3)伞绳、加强带和伞衣是弹性体,符合虎克定律;
4)不考虑伞衣透气性。
2. 数值模拟软件及算法介绍
本模拟采用的是显式动力学LS-DYNA 软件,其特点是具有强大的非线性能力,拥有大量不同种类的单元模型、材料模型和算法选择,能够很方便地处理各种高度非线性问题。到目前为止,LS-DYNA是对降落伞充气过程进行仿真的最优工具之一。
LS-DYNA 971是一个主要的程序版本。它增加了透气性材料的流固耦合算法,这样就可以通 过控制流固耦合过程的各个参数,真实地模拟降落伞的充气过程。 LS-DYNA与一般的CAE辅助分析程序操作过程相似,LS-DYNA的一个完整的显式动力分析过程包括前处理、求解以及后处理3个基本操作环节,并且前后处理均可以在官方强大的LS-PREPOST中完成,大大降低工作强度。
对于LS-DYNA的数值模拟算法,一般按照选用的算法分类,可以分为拉格朗日方法和欧拉方法。这两种算法的主要区别拉格朗日算法全局坐标系与物质是固结的,并且随着物质运动而运动,能够比较准确的描述占据在不同网格中的材料在整个计算过程中的不同应力过程,对于不同部分的材料可以相对自由的选择材料本构。
另外,由于拉格朗日算法方程中不存在对流项,结构形式相较于欧拉或者别的算法相对简单,有较高的计算精度,得到的流动图案比较精细。但拉格朗日算法也存在一定缺点,当物质有较大的位移时,会产生大变形,拉格朗日网格将会产生较大畸变,产生负体积,导致计算错误停止。
欧拉算法是坐标系固定,即网格固定,材料可以自由在网格间流动,网格不会因为物质的运动而变形的,该方法优点在处理大变形问题时,由于网格不动,不会产生较大的畸变,网格可以全程保证较好的精度,因此,欧拉算法能较好的处理大变形问题。但是缺点也很明显,由于各种材料填充在区域网格之中,两种会两种以上的材料经过流动后,分界面难以区分,并且对于材料的变形不跟随网格,难以追踪。
无论是欧拉方法还是拉格朗日方法,在处理不同问题的时候各有优缺点,在面对工程问题的时候,往往结合两者的优点,所以当前比较主流的方法是同时兼顾拉格朗日和欧拉两者优点的算法,比如最近几年被大家广泛采用的任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)、相容拉格朗日-欧拉(coupled Lagrangian-Eulerian,CLE)等方法。
目前为止,运用拉格朗日方法的流体动力学程序也在不断引入新的算法,与之同时也吸收了一些欧拉方法的优点,得到了很大的发展。相比之下,传统运用欧拉的程序算法却较为落后。本文采用的为任意拉格朗日-欧拉(ALE)算法,其特点是计算过程中网格点可以随材料一起运动,也可以在空间中固定不动,甚至还可以做到网格点在一个方向上固定,另一个方向上随物质一起运动。
在解决流固耦合问题时,即简称ALE方法LS-DYNA,采用关键字*CONSTRAINED_ LAGRANGE_IN_SOLID 实现固体与流体间的耦合。采用流固耦合算法模拟问题时,往往要对 Lagrange 算法中的固体结构进行约束,将固体结构的相关参数传递给流体单元。
在 LS-DYNA 中数值模拟降落伞的充气过程时,固体结构的主要约束方法是罚函数耦合约束。对于罚函数约束而言,其原理是耦合系数追踪 Lagrange节点(结构,即从物质)和 Euler 流体物质(主物质)位置间的相对位移,顾名思义罚函数为惩罚函数,先给一个位移,一般是从物质穿透于主物质,然后在一个或若干个分析步中拉回,以此完成整个流固耦合分析。
3. 数值仿真模型建立
3.1降落伞仿真模型建立
3.1.1几何及有限元模型
具体见上图3,采用壳体单元四边形网格,对单个伞面进行扫略画法,单个伞衣一共有XX个单伞叶组成,每个伞叶网格如下图,每个伞叶网格数量为17024,四边形壳体单元(*ELEMENT_SHELL_THICKNESS),单元算法的控制关键字为*SECTION_SHELL,伞衣一共510720,最大网格尺寸为0.15m,最小网格尺寸为0.02m,保证伞衣尾部和头部节点数一直,且单片伞面网格数量完全相同,以此尽可能模拟每片伞叶均匀展开。伞衣材料属性由*MAT_FABRIC关键字来定义。
伞绳为离散的梁/索单元(*ELEMENT_BEAM),单元算法的控制关键字为*SECTION_BEAM,网格大小尺寸均匀,为0.5m,伞绳与重物连接绳分别赋予不同单元属性,共1530个单元。伞绳材料属性由*MAT_CABLE_DISCRETE_BEAM 来定义。伞绳汇交点同样采用共节点建立接触,重物连接绳与伞绳共节点,初始状态太约束该节点的Z向自由度,即垂直方向,以此保证降落伞在开始展开阶段流向与空气流向一直,保证伞面顺利展开,具体约束时间为0.1s,采用关键字* B O U N D A RY _ SPC_NODE 来进行约束。




图 4 单伞片、伞绳、伞衣网格划分
3.1.2流场域及边界条件设置
流场仿真模型形状选用圆柱形流场,如图 5所示,其尺寸大小需满足70m总长的伞衣、伞绳、重物绳、重物在一定初速度下运动3s且不出流场边界,其基本的几何尺寸确定 如下:
流场半径R=25m;流场长度 L=180m;
流场采用六面体扫略网格结构化网格,设置除底面外的流出边界,保证流固耦合时的空气压力不会从底面泄露,网格尺寸大小为0.2m,共87万流体网格,通常在处理流固耦合问题时,流体网格尺寸需大于结构体2倍,假定伞面网格平均尺寸为0.1m,流体定义为0.2m,满足流固耦合的最佳单元匹配,从而使流固耦合经常遇到的泄露问题概率降到最低。

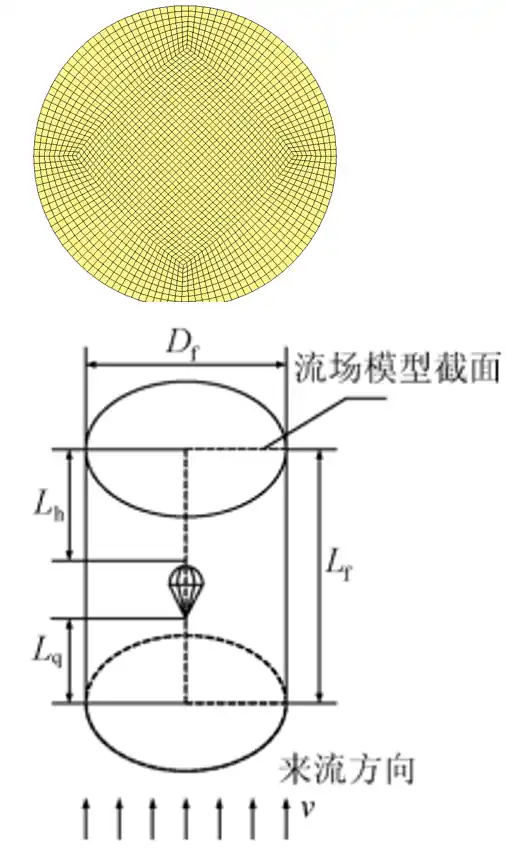
图 5 流场域大小确立
3.1.3流场域及边界条件设置
对于空气域采用六面体体单元,在LS-DYNA中体单元控制关键字为 *SECTION_SOLID,其中ELEFORM设置为11用来模拟欧拉流体。实际工况中空气域应当是无限大的,因此不会出现流场中的压力因流出而减少,但是在数值模拟中受到计算量的影响,不得不设置特定区域的流体域,这种做法的弊端会出现压力因流出边界的设置而减小,必须在流场前端增加一层流体压力入口单元,其主要作用是向流场中源源不断地输入恒压、恒速的流体,一般做法是在流场单元算法参数的选择*SECTION_SOLID中ELEFORM设置为11,AET设置为4。
本文为流体单元选择的是单点 ALE 方法的多物质单元方程。一般类似空气或者水域流体选用*MAT_NULL 的材料本构,且选择对应的状态方程组合模拟表征材料的体积变形与压力之间的关系。空气的状态方程用*EOS_LINEAR_POLYNOMIAL来定义。 流场仿真模型的流场入口单元区域用 *BOUNDARY_PRESCRIBED_MOTION_SET 来施加对单元的强制运动,使得流体压力入口单元获得恒定的速度。
4. 降落伞充气过程的仿真结果及分析
4.1 降落伞充气过程的数值模拟
4.1.1单降落伞充气展开过程

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删