前言:
铆接工艺在汽车连接工艺中具有广泛的应用,包括白车身、发动机罩、行李箱盖板、天窗等等位置都可以应用铆接工艺。铆接工艺具有以下几个特性:1.应力集中小,动态疲劳强度高;2.具有较好的撞击吸能特性;3.可以铆接带有夹层/胶层的材料组合;4.可以实现在线铆接质量监控等。
尤其是在当今社会的发展形势下,减排降耗的需求日益增加,车身轻量化设计也越来越受到关重。铆接工艺能够在以下几个方面解决车身轻量化问题:1.可实现不同形态材料之间的连接工艺问题,与焊接等其他连接工艺相比,铆接是连接有色金属的最佳选择。这便给车身轻量化材料的应用带来了可能。2.解决不同形态材料之间的连接强度和安全问题,铆接工艺充分满足静态强度和动态疲劳强度要求,且具有撞击吸能特性,克服焊接不足,满足安全方面要求;3.解决车内噪音和防水问题,允许不同形态材料之间具有涂胶,起到隔音和防水的目的。4.可连接的材料包括铝材(铸铝、型材、板材),深冲压钢、高强钢、镁、铜以及非金属材料等。
一、自穿刺铆接设备和工艺
自穿刺铆接设备主要包括:夹具、冲头、自穿刺铆钉、连接材料、底模。

自穿刺铆接的工艺过程包括:定位、加紧、施压、穿刺、变形、成型等6个步骤。工艺连接过程简单快速,铆钉在外力的作用下,通过穿透第一层材料和中间材料,并在底层材料中流动和延展,形成一个相互镶嵌的塑性变形的铆接连接过程,称为自穿刺连接,具有较高的抗拉强度和抗剪强度。

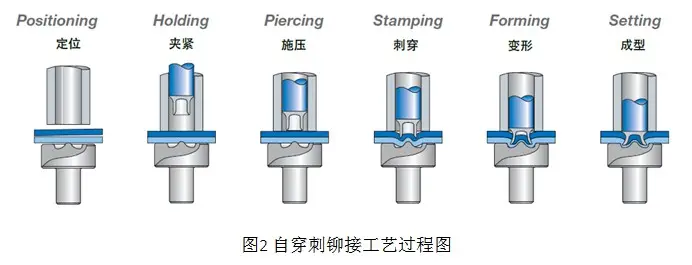

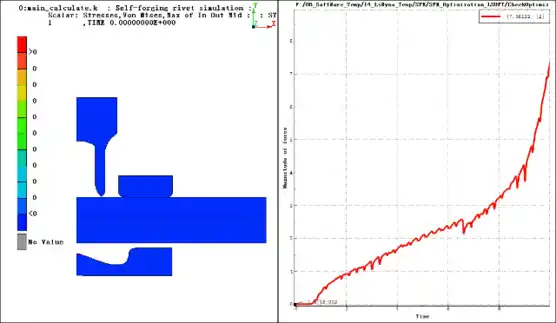
图3 SPR工艺过程

图4 SPR工艺过程监控
二、设计要求
2.1 互锁值a
为了保证连接强度、互锁值要满足一定的设计要求。如:铆钉长度规格为5mm时,要求互锁值a1、a2≥0.15 mm,铆钉长度规格为3mm时,要求互锁值a1、a2≥0.10 mm。

2.2 铆钉和连接材料要求
铆钉和连接材料不可以发生裂纹,因此需要控制铆钉和连接材料的应力和应变值。


自穿刺铆接在车身上的应用案例:

四、基于LSDYNA的SPR连接工艺过程仿真
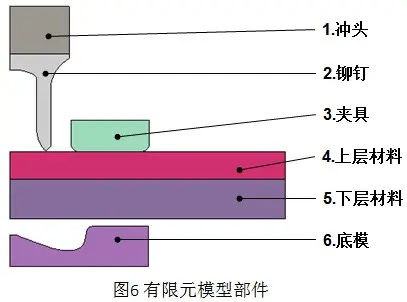
4.1 有限元模型
为了提高计算效率,将SPR连接过程分析简化为2维轴对称模型。有限元模型包括1、冲头;2、铆钉;3、夹具;4、上层材料;5、下层材料;6、底模等6个部件。
有限元模型共有11721个单元、12398个节点,其中铆钉为钢材,连接板材料为铝材,冲头、夹具和底模为刚性材料。分析采用kg、mm,ms,KN、GPa单位制。

关键字设置:
1.通过*CONTACT_2D_AUTOMATIC_SINGLE_SURFACE_ID关键字,创建除了冲头外所有部件的自接触。

2.通过*CONTACT_2D_AUTOMATIC_SURFACE_TO_SURFACE_ID关键字,创建冲头与其他部件的接触。
3.通过*SECTION_SHELL elform=15定义轴对称单元。
4.在铆接过程中,铆钉会穿透上层材料,通过关键字*PART_ADAPTIVE_FAILURE定义上板材料在满足最小厚度设置值0.1mm时断裂。
5.在铆接过程中,上下板将会发生严重的塑性变形,为了保证计算成功,需要使用LSDYNA的自适应网格变形技术。通过关键字*control_ADAPTIVE定义上下板材料网格自动重构参数。
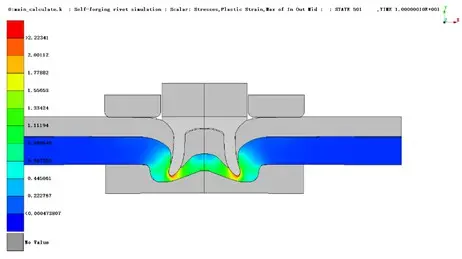
4.2 分析结果
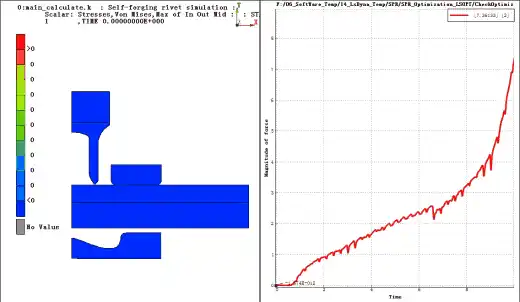
铆钉应力结果:
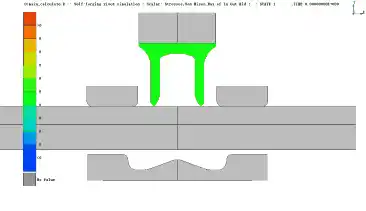
下板材料等效塑性应变结果:
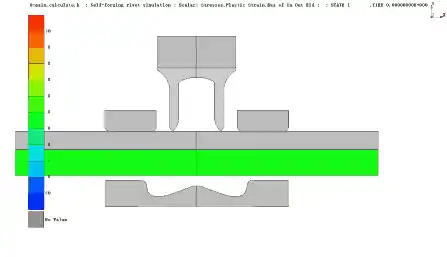
铆接力结果:
互锁值:

五.基于LS-DYNA和LS-OPT的多目标优化
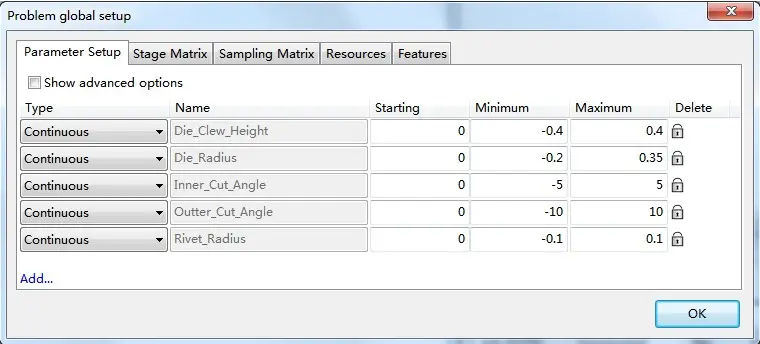
5.1 设计变量
针对铆钉和底模共建立5个形状参数变量,包括:1、铆钉外切角;2、铆钉内切角;3、铆钉内半径;4、底模内凸高度;5、底模内半径等5个参数。见图8。


图 基于网格变形技术创建的铆钉参数化模型

图 基于网格变形技术的底参数化模型
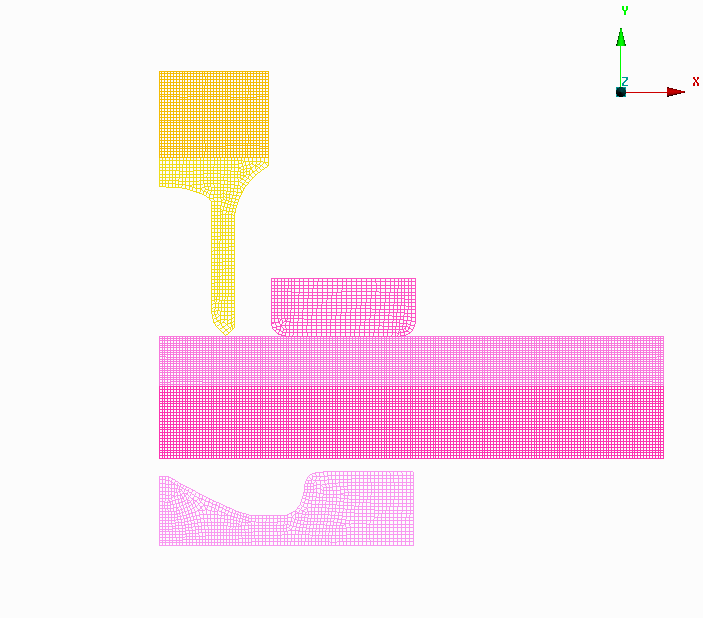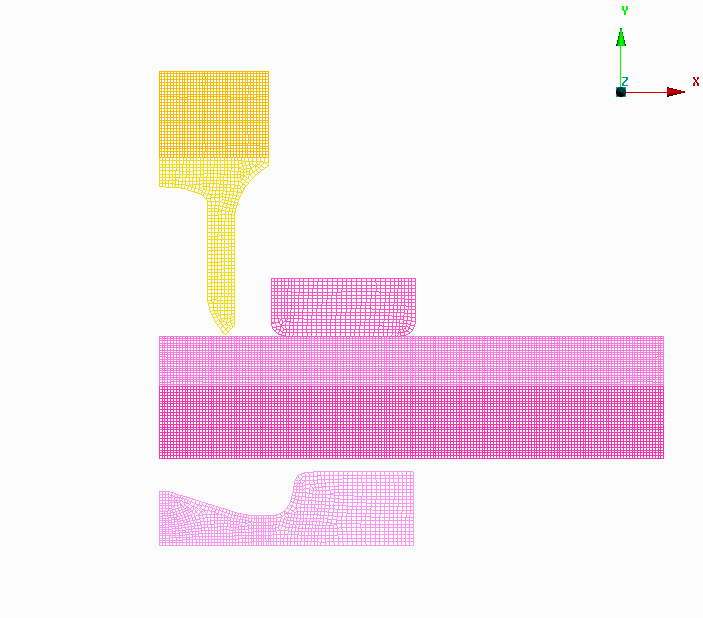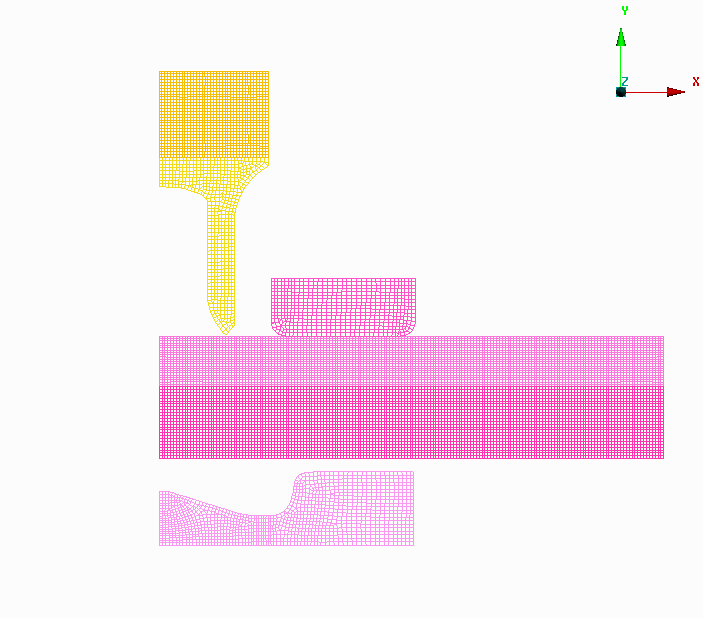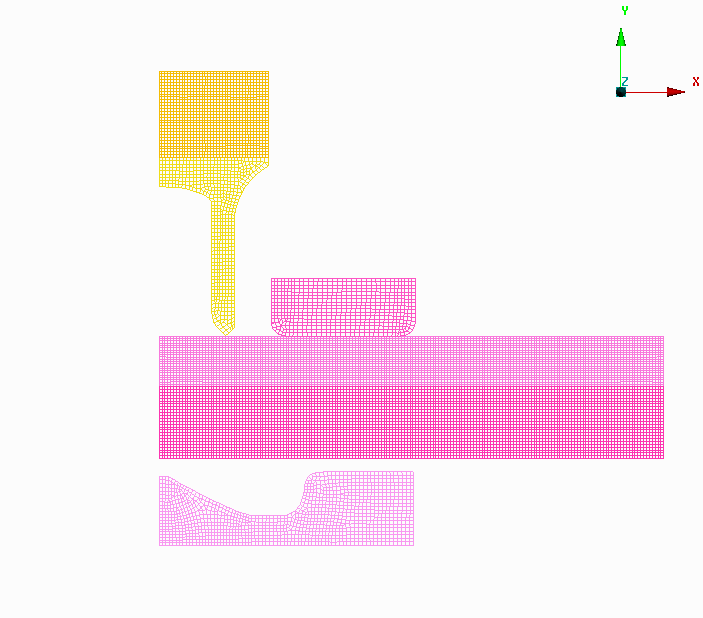
图 参数化求解模型
5.2 设计响应
设计响应包括:
1、铆钉最大应力;
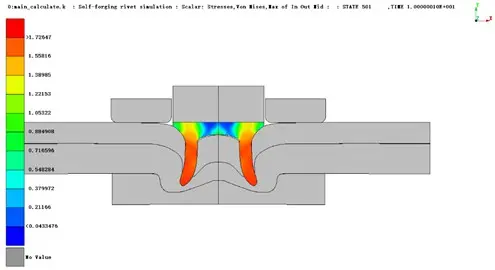
2、下板材料最大等效塑性应变;
3、最大铆接力;

4、互锁值;

前三个设计响应可以通过常规后处理方法获得,对于互锁值是通过铆钉和下板材料的特定节点间距的X分量得到。由于下板在计算过程中进行网格重构,因此单元和节点号是变化的。为了获得互锁值结果。需要通过python二次开发来完成,在后处理软件中获得互锁值设计响应。python脚本为:
def main():
model_id = 0
all_resultsets = results.Resultsets(model_id)
result = all_resultsets[-1]
part_type = constants.PSHELL
part1_nodes = nodes.NodesOfPart(model_id, part_type, 1)
part6_nodes = nodes.NodesOfPart(model_id, part_type, 6)
for n in part1_nodes:
if nodes.CoordinatesOfNode(result, n.id).y < 9.7:
if nodes.CoordinatesOfNode(result, n.id).x > node1_x:
node1_x = nodes.CoordinatesOfNode(result, n.id).x
node1_id = n.id
for n in part6_nodes:
if nodes.CoordinatesOfNode(result, n.id).x > 3.12 and nodes.CoordinatesOfNode(result, n.id).y > 7.85:
if nodes.CoordinatesOfNode(result, n.id).x < node6_x:
node6_x = nodes.CoordinatesOfNode(result, n.id).x
node6_id = n.id
dis = node1_x -node6_x
if __name__ == '__main__':
main()5.3 设计目标
多目标设置为最小化铆钉最大应力、最小化下板最大等效塑性应变、最小化铆接力、最大化互锁值。
5.4 LS-OPT多目标优化

LS-OPT优化流程图
设计参数设置

设计目标设置
在提取结果时,由于设计点可能会出现计算错误等造成的结果不正确的情况,因此需要在提取设计响应结果时判断计算是否正确并得到了正确的结果。这里通过Python脚本来实现该功能:
import os
with open('getresults.ses.results','r') as g:
for line in g.readlines():
if "Max_Stress" in line:
stress = line.split(",")[2]
if "Max_Strain" in line:
strain = line.split(",")[2]
g.close()
if float(stress) > 0:
os.system("echo 'N o r m a l'")
else:
os.system("echo 'E r r o r'")优化算法选择遗传算法,代理模型方法选择径向基函数法,样本点选择LSOPT自带的空间填充法。其他保持默认设置。
5.5 优化结果
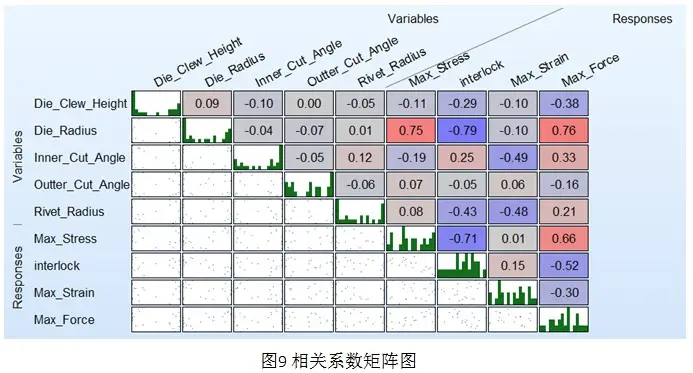
相关系数矩阵图为设计变量和设计响应直接的相关系数,有不同的颜色和数值表示。颜色从蓝色到红色变化。蓝色表示负相关,红色表示正相关。颜色越深相关系数越大。从相关系数矩阵图结果可以看出,最大应力和底模半径相关系数最大,为正相关;底板材料最大等效塑性应变和铆钉内切角相关系数最大,为负相关;最大铆接力和底模内半径相关系数最大,为正相关;互锁值和底模半径相关系数最大,为负相关。
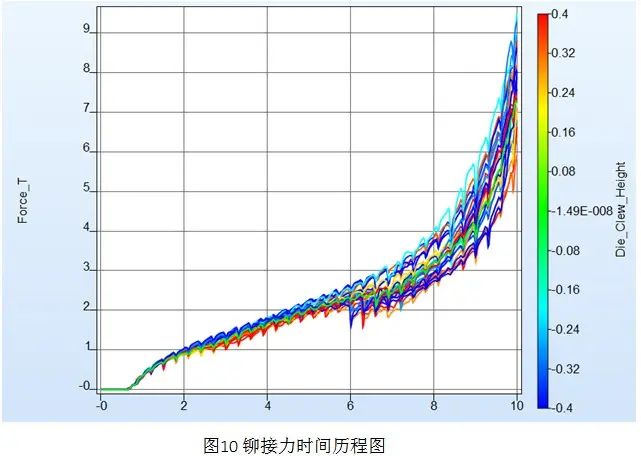
图中铆接力具有规律性的波动,是由于在求解过程中上下板不断进行网格重构,引入了解的噪声。
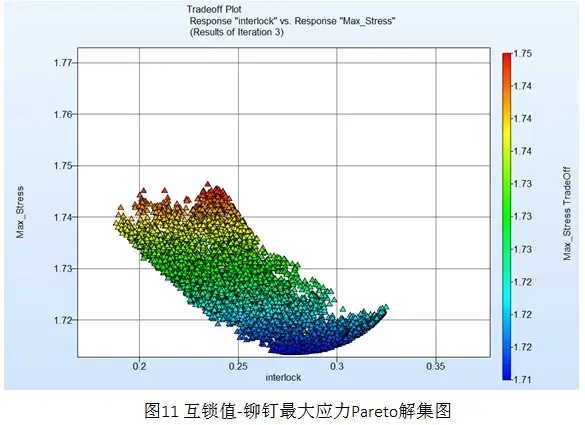


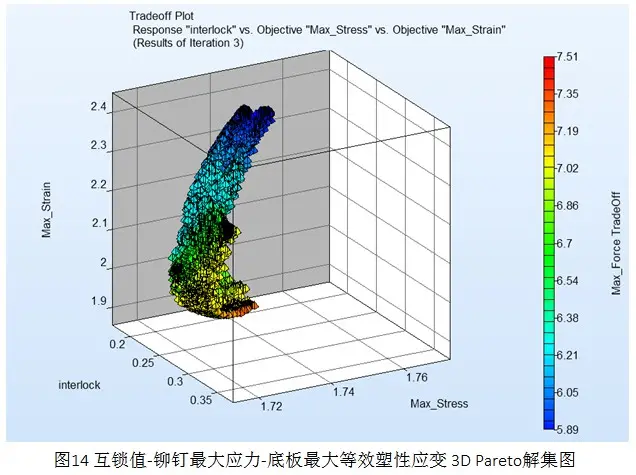
从3D Pareto解图中可以得到满足一定目标的最优解。如其中一个优化解为:


图中蓝色为原始模型,红色为优化解更新模型。

图 铆钉应力结果对比(左侧为原方案结果)

图 底层材料等效塑性应变结果对比(左侧为原方案结果)
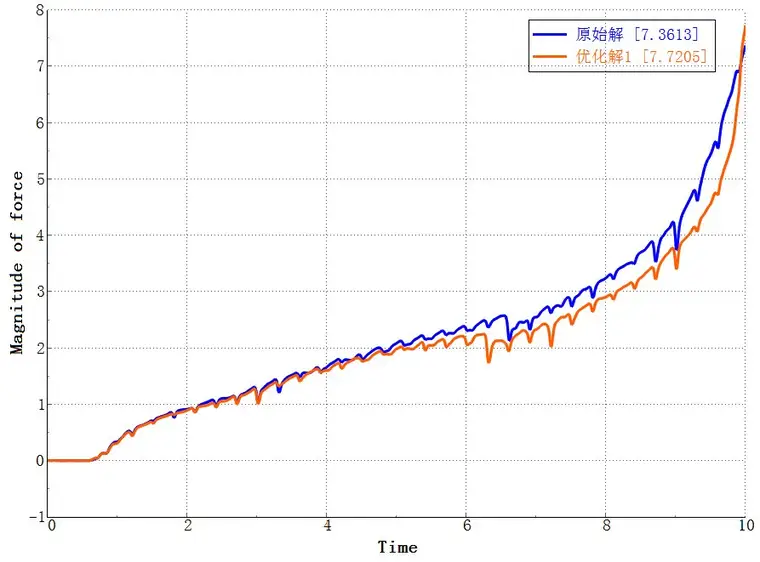
图 铆接力结果对比
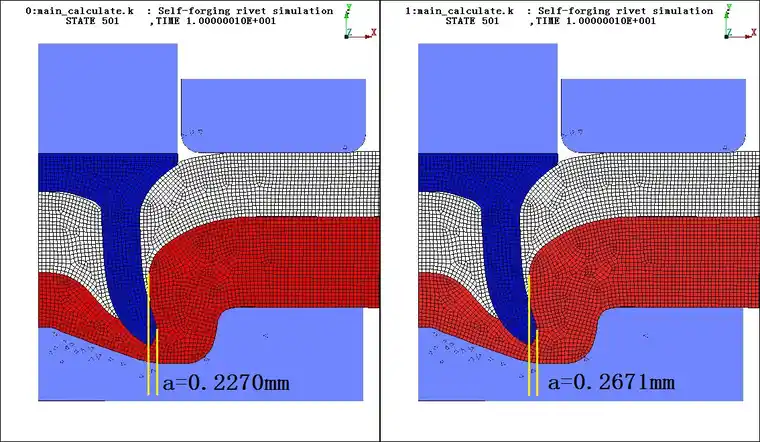
图 互锁值结果对比(左侧为原方案结果)

选择以互锁值最大化为主要目标的一组解,互锁值从0.2270增大为0.2671mm,性能提升17.67%,同时铆钉最大应力、底板最大等效塑性应变和最大铆接力性能变化分别为0.38%、-1.08%和4.88%。
结论:
1. LS-DYNA显式分析具有精度高,求解效率高等优势,适用于自穿刺铆接工艺过程等仿真分析。
2. LS-DYNA的自适应网格变形技术可以解决自穿刺铆接过程连接板大变形造成网格畸变无法正常求解的问题。
3. LS-OPT具有高效的优化效率,多目标优化针对自穿刺铆钉和底模的参数化模型进行优化,寻找铆钉应力、底板材料等效塑性应变、铆接力和互锁值的最优解。如为了提高互锁值选取一组优化解,互锁值从0.2270增大为0.2671mm,性能提升17.67%,同时铆钉最大应力、底板最大等效塑性应变和最大铆接力性能变化分别为0.38%、-1.08%和4.88%。
4. 基于LS-DYNA的自穿刺铆接多目标优化仿真可以有效地指导自穿刺铆接工艺优化设计。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删