1.工程背景
随着半导体行业的蓬勃发展,单晶碳化硅作为典型的第三代半导体材料被广泛应用于集成电路生产、光学衬底材料制备等加工过程中,晶片表面质量的好坏直接决定了半导体器件的使用性能及工作寿命[1-2],这也就对以单晶碳化硅为代表的光学材料的加工质量提出了更高的要求,其中在研磨抛光过程中产生的表面/亚表面损伤缺陷(见图1-1亚表面损伤示意图)是影响晶片性能的重要因素,而对损伤层(SSD)中的裂纹产生、扩展表征与控制更是不容忽视。
通常,通过研磨抛光单晶碳化硅晶片实验来观测裂纹是行之有效的手段,但裂纹产生、扩展是一个复杂的动态过程,通过实验后观测的手段显然与晶片表面裂纹扩展的真实情况相差甚远,其次单晶碳化硅属于典型的硬脆材料,其在加工过程中的裂纹产生、扩展往往在微秒间完成,这也是难以用实验的手段对裂纹扩展进行观测的另一原因。
因此本文采用ANSYS/LSDYNA软件建立了单颗磨粒划擦单晶碳化硅模型,通过仿*真手段来分析单晶碳化硅在研磨加工过程中的裂纹产生及扩展情况。


2.研磨加工模型分析及模型简化
2.1研磨原理
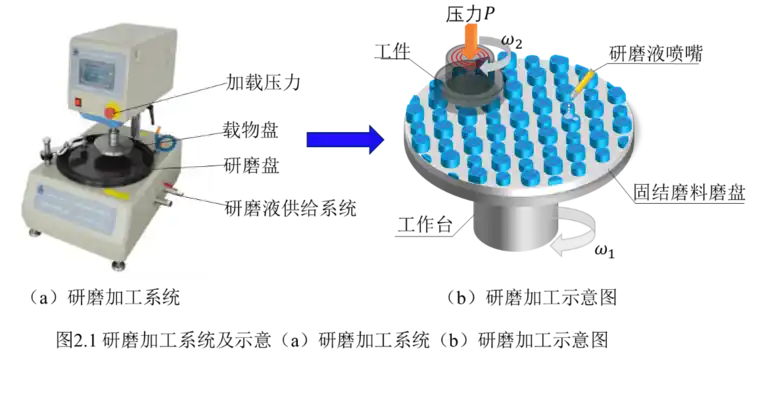
固结磨磨料研磨加工系统主要由研磨盘、载物盘、研磨液供给系统组成。研磨时,向下压力P使紧贴上盘面作自转运动的工件与下盘面接触作公转,依靠相对运动实现磨粒对工件的研磨加工[3]。研磨加工系统及示意图如图2.1所示。本文所采用的图案磨盘为课题组自行设计的双图案排布磨盘,在实验中表现出比传统图案磨盘更高的效率和加工精度,其微粉金刚石磨粒通过钎焊技术排布在磨盘上,钎焊效果图如图2.2所示。此外因研磨相对磨削具备更低的转速,在加工过程中的散热及振动很小,故忽略加工系统的振动及研磨液对磨粒加工的热作用。

2.2模型简化
为了使仿真模型更加准确反映实际磨粒加工导致的损伤及裂纹扩展情况,做出如下三点模型简化,最终模型简化示意如图2.3所示。
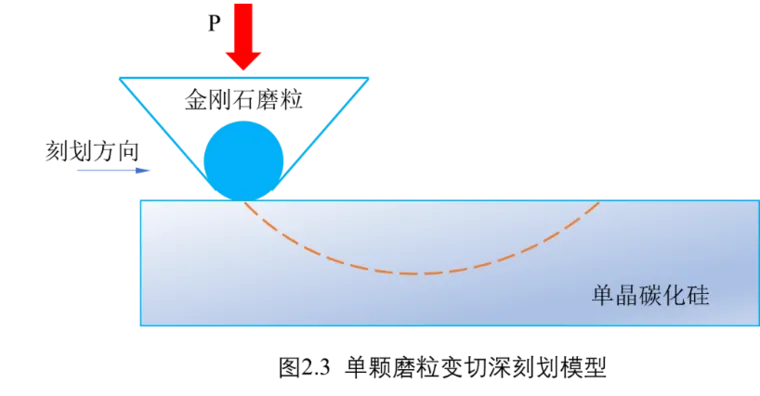
1)研磨过程简化成单颗磨粒对工件的变切深刻划过程,磨粒设为圆锥状,工件设为长方体。理由:研磨是通过磨盘上的微粉金刚石磨粒与工件之间的相互冲击、划擦等力学物理作用来去除材料(见图2.1),因此,将研磨盘加工等效为单颗磨粒加工;在极短时间内研磨盘的复杂运动可以等效为直线划擦运动;此外根据实际金刚石磨粒压头形状,将磨粒设为圆锥形状,工件设为长方体。
2)忽略加工系统的振动及工件材料的热传导。理由:研磨相对磨削具备更低的转速,在加工过程中的散热及振动很小。
3)磨粒设为刚体。理由:磨粒为金刚石材质,为自然界最硬的物质,其硬度、强度远远大于单晶碳化硅。

2.3模型几何尺寸
刻划实验中采用圆锥角为120°,圆锥倒角半径0.2mm的金刚石压头,故仿真中设置磨粒特征尺寸与之相同。工件尺寸与磨粒特征尺寸配合到同一尺度下即可,均为mm级,设为2×1×0.3mm3。
长方体工件(长×宽×高):2.0mm×1.0mm×0.3mm
圆锥磨粒尺寸:圆锥角 120°,圆锥倒角半径R=0.2mm
120°,圆锥倒角半径R=0.2mm
3.仿真方法
3.1仿真算法选择
FEM-SPH(Finite Element Method-Smoothed Particle Hydrodynamics)耦合算法,即有限元-光滑质点流体动力学耦合的方法。
本文所用的加工材料单晶碳化硅属于典型的硬脆材料,对于硬脆材料的研磨加工仿真,单纯用有限元法(FE)来模拟往往会因为网格畸变而导致计算精度低甚至计算强行终止的情况。这是因为在磨屑的形成过程中,材料的去除会经历弹性变形阶段、弹塑性转变阶段、塑性变形阶段、塑脆性转变阶段及脆性断裂,且这一过程中工件材料会产生大量的不连续裂纹。因此,网格划分的精度及材料失效判据的参数选取直接影响了模型计算的精度与效率,而采用SPH方法则避免了上述问题[4]。
SPH方法是一种纯Lagrange方法,其基本思想是:将连续的流体(或固体)用相互作用的质点组来描述,各个物质点上承载各种物理量,包括质量、速度等,通过求解质点组的动力学方程并跟踪每个质点的运动轨道,求得整个系统的力学行为。
SPH用质点代替了网格,因此不会出现网格大变形问题,同时采用SPH方法进行建模不受尺度的限制,对于微纳尺度的动态仿真(本文工件模型尺寸为μm级)结果仍然具有较高可信度。但FE方法在计算效率上相比SPH方法仍然具有极大的优势,因此本文采用FEM-SPH耦合方法建立单颗磨粒划擦单晶碳化硅模型。
3.2仿真流程
本文选用ANSYS 19.0版本进行模型建模相关操作,全程建模均采用统一的g-mm-ms单位制。首先,在Workbench中选用Workbench LSDYNA模块,完成磨粒和工件的有限元模型工作。然后忽略其他信息,直接将该模型保存为x_t格式导入到ANSYS 经典版中,选用ANSYS/LSDYNA模块进行单元、材料参数、网格划分工作;单元选用显示3D SOLID164实体单元,另外选择显示Thin Shell163单元用于圆锥模型的映射网格(mapped)划分,之后设置金刚石磨粒的材料本构(rigid),包括:密度、杨氏模量、泊松比;工件的材料本构选用JH-2模型,由于ANSYS/LSDYNA中并没有此种本构模型,故本文采用替代法设置:即先赋予工件一种弹性材料本构方便后续网格划分,模型检查等工作,之后通过在LSDYNA的二次开发软件LS-PREPOST中修改导出的K文件,将工件弹性材料本构再次替换成JH-2本构,完成工件材料的材料赋予。
完成单元、材料定义后,在对模型进行网格划分,磨粒采用mapped划分,工件采用六面体网格划分,网格划分完成后可以通过Part options查看工件Part的总网格数对模型网格大小(精度)进一步调整;之后对仿真总时长、磨粒初始刻划速度、边界条件及自由度约束进行设置(这一步骤也可以在LS-PREPOST/UE软件中通过编辑关键字进行设置),之后对沙漏、动能、内能进行控制(一般设为默认),然后在ASCII OUTPUT中设置需要输出的物理量(能量、接触力、损伤等),最后写出K文件,然后在LSDYNA的LS-PREPOST前后处理模块打开保存的K文件,进行网格化工件模型到SPH工件模型的转化替换工作及关键字的删除、添加编辑,之后设定SECTION-SPH关键字,选用材料模型MAT 110(JH-2),设定材料模型所需参数,并将材料关联到工件Part;之后设定DEFINE-CURVE 关键字定义磨粒轨迹与速度并关联到rigid Part部分。
对磨粒的约束通过PRESCRIBED_MOTIOM_RIGID关键字定义,较为简单,而对SPH模型的约束不同于网格化模型,需定义BOUNDARY及 SPH_SYMMETRY_PLANE 关键字,对 SPH 质点采用虚粒子约束法,即在 SPH 质点周围假设仍有其他粒子对模型包围从而对其形成约束。对磨粒与SPH工件的耦合接触也不同于以往有限元网格模型,本文仿真应用了AUTOMATIC_NODES_TO_SURFACE 关键字进行定义。
对于工件损伤裂纹的查看需要借用UE编辑器修改EXTENT_BINARY关键字完成,将所有已经定义的关键字在 Part 中进行关联后,并用UE编辑器检查K文件后,整个求解模型及模型检查完成。
将上述结果仍保存为K文件格式,添加到 ANSYS 中的 LS-DYNA Solver 中进行最终求解计算,求解得出的 D3PLOT 文件用 LS-PREPOST 打开来获取应力应变云图、损伤图、接触力曲线等仿真结果。
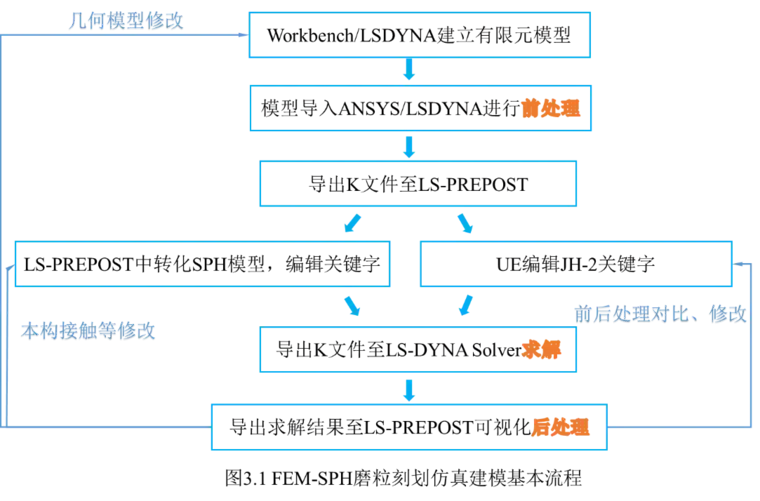
至此,磨粒划擦模型分析基本结束,为了后期方便对模型修改,本文中的关键字修改可采用UE编辑器替代LS-PREPOST对K文件的编辑工作,其优点是避开繁琐的多次软件的打开、关闭及保存操作,直接在软件底层对关键字命令编辑,省时高效。建模流程如图 3.1所示。
3.3仿真难点
1)网格化工件到SPH工件的粒子化转化与粒子间隔的控制(前后模型尺寸不变、材料相同(包括本构替换和密度替换)、粒子间隔可控制)
对于磨粒仿真,一般采用分部建模法:在ANSYS软件中建立磨粒的有限元模型,在LS-PREPOST软件中建立工件的SPH模型,但此种建模方法不利于后期模型尺寸的对比修改,故本文采用集中替换法,即直接在ANSYS WORKBENCH中建立磨粒和工件的有限元模型,之后在LS-PREPOST软件中进行SPH转化与替换。这样处理的优点是:便于在同一建模环境下(ANSYS 建模环境)对几何模型尺寸的对照修改与集中编辑。在ANSYS中建立好磨粒、工件系统模型后在LS-PREPOST中进行FE-SPH转化,如图3.2所示。
为了仿真计算的准确性,在FE-SPH转化过程中,应满足:前后模型尺寸不变、材料相同(包括本构替换和密度替换)、粒子间隔可控制3个条件。对应软件操作:在LS-PREPOST中编辑SPHGEN关键字创建SPH模型,并选择Solid Nodes创建方法;之后在密度(Den)一栏填入单晶碳化硅的真实密度(g-mm-ms单位制下)完成材料密度的替换;
最后通过UE编辑器编辑保存的K文件,将预设的弹塑性材料修改为*MAT_110号材料(JH-2本构)完成本构替换。另外,为保证SPH粒子间隔的可控性,SPH粒子间隔h0与替换前的有限单元网格大小应具有确定的对应关系,图3.2给出了一种对应方法(即上文提及的Solid Nodes创建SPH法):有限网格单元的4个节点(分别表示为1、2、3、4)对应转化为4个SPH粒子,同时网格大小等于粒子间隔长度h0。
那么在ANSYS进行网格划分时就可以通过设置不同尺度的网格来控制SPH粒子间隔h0(l=h0),这极大方便了本文仿真模型中对于切深的设置(见本文表1所示)。

2)单晶碳化硅的损伤参数如何输出、裂纹的云图后处理如何显示
JH-2本构模型包含有关于硬脆材料的损伤失效模型算法,因此无需另外定义单元失效准则就用模拟出单晶碳化硅的损伤及裂纹扩展现象。这也是JH-2本构能够模拟单晶碳化硅加工裂纹扩展的本质原因。
为了更好地输出损伤参数,在仿真计算中首先识别非损伤区与损伤区,将断裂应变满足D1[P*+T*]D2
≥Efmin的SPH粒子标红,以示区别,这部分区域就表示加工过程中的损伤。之后将输出裂纹的损伤参数定义附加写入D3PLOT文件的时间历程变量数目(history #2)。软件操作步骤:用UE编辑器编辑关键字*DATABASE_EXTENT_BINARY,将第2个时间历程变量修改为2(即NEIPH=2),该参数就表示陶瓷材料的损伤参数。对应的关键字编辑如下:
*DATABASE_EXTENT_BINARY
$NEIPH,NEIPS,
2,0
3)SPH工件边界的处理(“虚粒子约束”法)
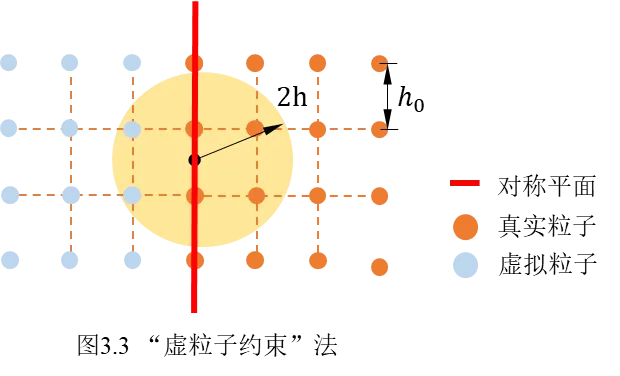
SPH算法是模拟大变形、防止网格畸变的重要手段,但相对FEM算法,其计算效率较低,同时SPH粒子的边界条件较难处理。对于此种问题,文献中[5]通常采用“虚粒子约束”法来定义SPH模型的工件,本文亦采用“虚粒子约束”法处理单晶碳化硅SPH工件的边界问题。
图3.3给出了“虚粒子约束”算法的基本原理:“虚粒子约束”法是对工件可能移动方向进行约束,靠近SPH粒子边界处2h(h为粒子光滑长度)范围内设置出虚粒子。对于靠近边界的SPH粒子,通过对自身的映射,自动创建具有相同质量、压力、绝对速度的虚粒子,使得真粒子能正常进行邻域搜索,以达到约束边界的目的。与之对应的关键字是*BOUNDARY_SPC_SYMMETRY_PLANE。
4)有限网格磨粒与SPH粒子化工件的耦合接触
不同于FE算法,本文中SPH模型以粒子代替网格,相当于有限网格的磨粒与粒子化工件的不连续加工过程。因此,FE的面面接触算法已经不再适用。本文对于有限元单元与光滑粒子接触界面的相互作用(磨粒与工件),则是通过罚函数算法来定义,耦合接触算法采用自动点面接触算法,主面设为磨粒,从面设置为SPH工件(MSTYP=3,SSTYP=4),其对应的关键字为*CONTACT_AUTOMATIC_NODES_TO_SURFACE。
本文针对接触算法经过多次仿真实验验证,得出结论:自动点面接触算法、侵蚀点面接触算法(*CONTACT_ERODING_NODES_TO_SURFACE)均可应用于FEM-SPH耦合模型的接触设置中,但自动点面接触算法的计算效率更高且计算不易报错。故本文最终选用自动点面接触耦合算法。
4.仿真参数
仿真参数的设置原则一般遵循三点[6]:一是计算时间合适,二是结合实际工艺参数,三是适当放大来凸显作用规律。
4.1加工参数的设置
本文中磨粒的变切深刻划是通过磨粒的运动完成,工件底面设为全约束。根据实际研磨实验中磨粒相对工件的速度、研磨盘直径及加工深度[7],并适当合理放大,设定磨粒的初始速度为50m/s,最大切深设为30μm,磨粒从切入工件到离开工件切深的变化范围为0-30μm。具体仿真参数的设置如下表1所示。
表1 仿真参数设置
| 参数 | 数值 |
| 工件尺寸 | 2×1×0.3mm |
| 切深(ap) | 0μm-30μm-0μm |
| 模型粒子数量 | 371280 |
| 粒子间隔 | 0.012mm |
4.2材料本构参数的设置
磨粒的本构设置较为简单,磨粒为金刚石,设为刚体(密度3560kg/m3、泊松比0.2、杨氏模量1000GPa),工件为单晶碳化硅材料,在碳化硅材料的变切深刻划过程中,材料的应力应变呈现非线性关系,这种情况下通常使用的弹塑性材料本构模型已经不再适用,目前针对陶瓷、碳化硅等硬脆性材料的研究,学者们普遍使用 Johnson 和 Holmquist 提出的 JHC(Johnson-Holmquist-Ceramic)本构模型(JH-2)来进行表征[7]。
此模型能够较为准确反映碳化硅加工过程中的动态损伤及裂纹扩展情况,适合本文的仿真要求。单晶碳化硅的 JH-2 材料本构模型参数是在查阅文献的基础上,通过多次模拟与实验验证获得的。表2给出了单晶碳化硅的本构参数。
表2 SiC的JH-2本构参数[6][9][10]
| 参数 | 取值 | 参数 | 取值 |
| R(kg/m3) | 3215 | EPSI | 1 |
| G(GPa) | 193 | T(GPa) | 0.75 |
| A | 0.96 | SFMAX | 0.11 |
| B | 0.35 | HEL(GPa) | 11.7 |
| C | 0.009 | PHEL(GPa) | 5.13 |
| M | 1 | BETA | 1 |
| N | 0.65 | K1(GPa) | 220 |
| D1 | 0.48 | D2 | 0.48 |
| K2(GPa) | 361 | K3(GPa) | 0 |
5.结果分析
5.1材料去除状态分析
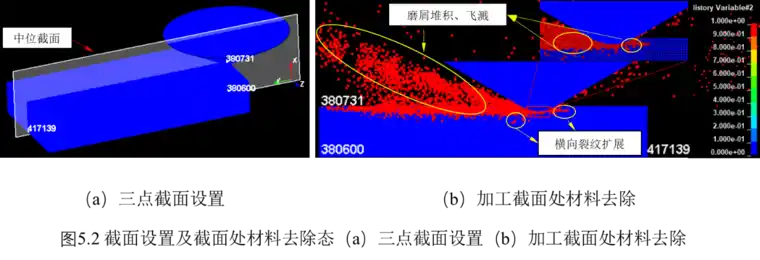
磨粒从0μm切深位置切入工件到工件的最大深度30μm处,之后做返程运动切出工件,在整个变切深刻划过程中(刻划距离50×0.04=2mm),材料的去除形态为“槟榔”形沟槽,由图5.1材料去除状态图可知:材料的去除方式主要为脆性断裂,磨屑的形状主要是粉末状。这主要是由于加工材料为单晶碳化硅,其高硬度和低断裂韧性导致材料很容易发生脆性断裂,加工磨屑因此呈现粉末形态,这也是其不同于加工铸铁等弹塑性材料形成的条状切屑的本质原因。在LS-PREPOST通过三点截面设置法(选取417139、380731、380600三点)观察磨粒加工截面[如图5.2(a)所示]发现:工件破碎深度大于最大切深30μm,磨粒两侧出现磨屑堆积。磨粒刻划过的区域磨屑堆积严重,磨粒未刻划区域也有少量磨屑堆积。这是因为工件以脆性断裂方式去除材料时,在Z向不断的压力作用下,裂纹向下扩展; 而X向磨粒两侧对工件的挤压效应是导致材料产生横向裂纹的原因,磨粒两侧的挤压使得工件内外产生应力差,工件受拉后在靠近磨粒侧面处产生横向裂纹,横向裂纹扩展到工件表面形成破碎,便产生磨屑堆积在磨粒两侧,具体如图5.2(b)所示。


5.2刻划力分析
在ANSYS对模型进行前处理时定义输出 RCFORC,即可用 LS-PREPOST 提取出单颗磨粒在变切深刻划过程中受到的切向力、法向力和轴向力。刻划力如图5.3所示。
分析:由图5.3(b)可知,X/Z始终小于1,法向力远远大于切向力;变切深加工过程中磨粒的切向力和法向力先随着位移的增大而增大,当位移为1.0mm左右时,两者力的大小开始减小,直至为0;而轴向力大小始终在0左右上下波动,基本不变。
这主要是由于磨粒刚与工件接触时刻划力为零,随着磨粒逐渐进入工件,切深不断增大,磨粒与工件的接触面积也随之增大,从而导致了切向力和法向力的增大,当磨粒切深减小时,磨粒逐渐向上运动离开工件,切向力和法向力又开始对称减小。划刻划力的波动则是由于磨屑的产生和飞溅所造成的。从图中也可看出,当位移为0.3mm左右时,法向力急剧增大,这表明工件已经出现脆性断裂。
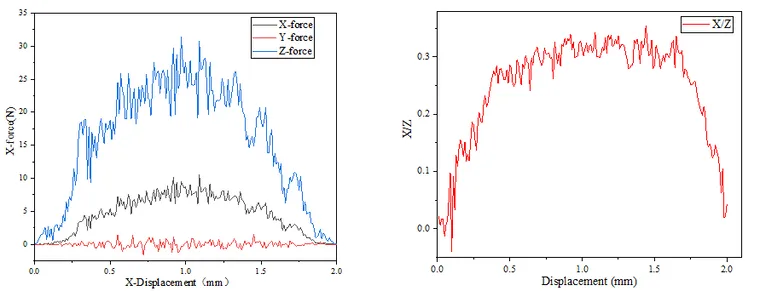

 图5.3 刻划力及力比(a)刻划力(b)力比
图5.3 刻划力及力比(a)刻划力(b)力比
5.3裂纹扩展分析
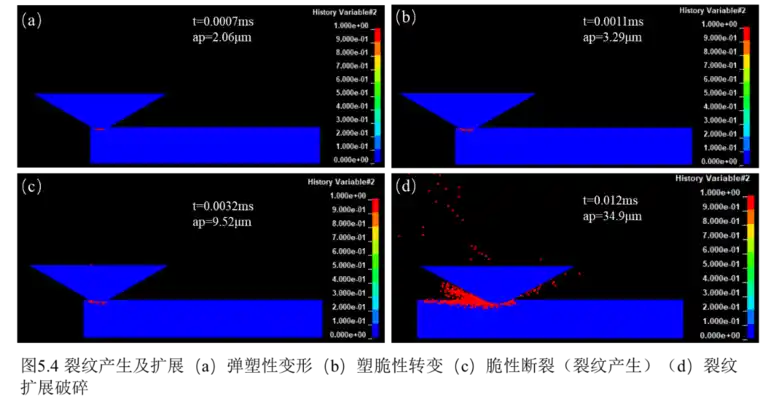
图5.4为不同切深下单晶碳化硅衬底的裂纹产生及扩展情况。从沿刻划方向(X向)的中位剖面图中可以看出,在t=0.7μs,磨粒切入工件2.06μm,可以看到工件表面刚刚开始出现相连的红色粒子,此时单晶碳化硅还处于弹塑性变形阶段,并没有出现裂纹;但t=1.1μs,磨粒切入工件3.29μm,红色粒子继续增加,而当t=3.2μs,磨粒切入工件9.52μm,红色粒子开始飞溅,表明工件表面开始出现脆性断裂,即裂纹开始产生;在这之后,工件进入脆性破碎加工阶段,磨粒下方的 SPH 粒子存在大量致密的且相连的红色粒子,说明出现明显的裂纹扩展现象。裂纹不断扩展、加深如图5.4(d)所示。
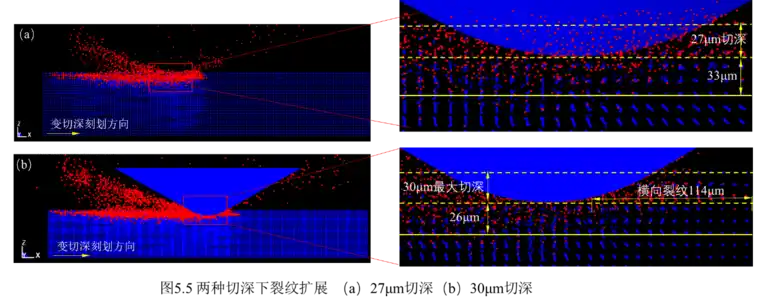
为了计算在不同切深下(27μm、30μm)裂纹扩展的深度,自t=3.2μs后(裂纹产生),对裂纹深度进行统计分析,如图5.5所示。
分析:从图5.5(a)中可以看出,在27μm切深范围内,可以发现大量相连的致密的红色 SPH 粒子,说明工件加工面存在明显的损伤。在 27μm切深下方约 33μm深的范围内也存在大量的红色 SPH 粒子,说明此时单晶碳化硅工件的亚表面损伤深度约为 33μm。虽然沿深度方向继续往下也能发现少量红色 SPH 粒子,但原本位置上的蓝色SPH 粒子并没有发生明显的位移,所以这部分区域没有发生明显损伤,而此区域的少量红色 SPH 粒子则是由于去除的SPH粒子飞溅溢散导致的。而在最大切深30μm范围内,大量红色SPH粒子致密相连更加明显,且工件表面出现114μm左右的横向裂纹,说明工件表面损伤愈加严重。此时损伤深度为26μm,有所减小,说明损伤深度并不是随着切深增大而增大的。
6.仿真结果验证
为了验证本论文中所建立的变切深刻划FEM-SPH 仿真模型准确性,应该进行仿真实验与理论分析和实际实验中的结果进行比较,当仿真实验结果与实际实验结果在规律和量级上保持一致时,认为本文中的仿真模型具备一定的准确性。
1)从材料能量变化上来分析材料去除变形及损伤的大小是在仿真中独有的优势和特点[10]。在LSPP中通过定义matsum可以查看SPH工件的能量变化。文献[11]指出,工件出现划痕是首先磨粒对材料挤压做功,使材料内部能量逐渐积累,当材料内部增加的能量难以维持平衡,材料开始对外做工,即出现材料变形和去除,而由于变形出现,对外做功,使材料内部能量下降。由图5.6可以得出:磨粒在开始与工件接触后,材工件内部能量迅速增长,形成尖峰,表明在研磨初期,磨粒能量完全被工件吸收且工件没有对外做工,因此表现为塑性变形,没有损伤和脆性断裂出现,之后工件能量急剧下降,表明此时脆性断裂出现,能量释放转化为磨屑动能、工件变形能、热等形式。这与前文通过损伤云图分析所得结果基本一致,同时验证了仿真结果的前后一致性。
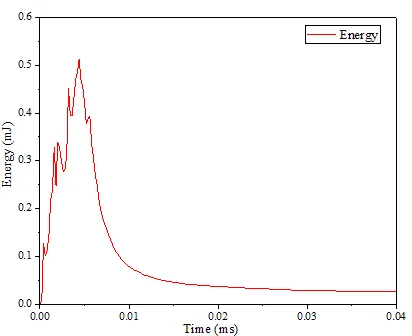
图5.6 工件能量变化图
2)法向力、切向力对比验证
对于磨粒的变切深刻划仿真中的法向力,可以通过金刚石磨粒划擦试验输出法向力、切向力与其对比来验仿真力的准确性。文献中[12]实际实验所得到的稳定状态下法向力最大为20N左右,切向力最大为5N大小左右。图5.7为本文仿真得出的力-时间曲线图。对比可以发现仿真中的法向力最大为25N左右,切向力最大为10N左右,与文献中的实验结果数值处于同一量级,且数值上较为接近。由此验证了本文仿真仿真模型的准确性。
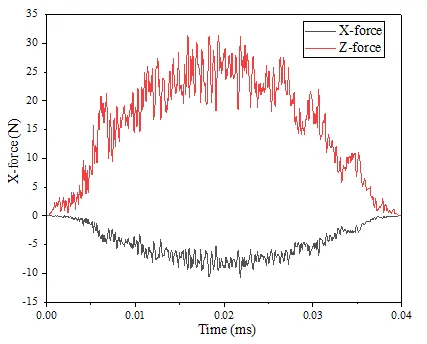

图5.7 仿真刻划力
7.结论
1)由 FE-SPH 仿真结果可知,当磨粒切深为30μm 时,单晶碳化硅以脆性去除为主,工件存在明显的亚表面裂纹和破碎现象,损伤深度约为26μm;当磨粒切深小于9.52μm 时,单晶碳化硅工件不存在明显的亚表面裂纹。因此可以通过控制磨粒切深来实现工件的塑性加工,减小损伤从而提高表面质量。
2)损伤深度与磨粒的切深并非呈正相关规律,在一定范围内,随着切深的增大,工件损伤深度增大,但切深超过一定值时(30μm)损伤深度有可能减小。
3)仿真所用本构为JH-2理想模型,虽然能够用于模拟单晶碳化硅材料,但实际实验中材料内部不可避免存在缺陷,如空隙、微裂纹等,因此仿真结果与实际实验不可避免存在一定的误差。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删