超高音速飞行时会在物体头部形成弓形脱体激波,激波后会发生各种化学反应,空气组分发生离解、复合和电离,飞行器表面的防热烧蚀材料在高温、高热流作用下烧蚀,形成化学组分多样、化学反应复杂并且热力学状态剧烈变化的复杂流场。典型的高超音速绕流流场如图1所示。

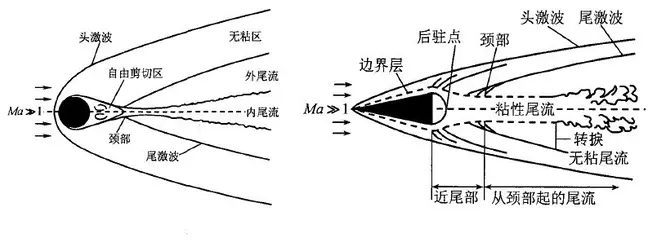
图1 高超音速钝体典型绕流流场
当超高音速流场中空气电离度达到一定程度时,电离气体表现出等离子体所具有的集体行为而成为等离子体,称为等离子体鞘套。通常所说的等离子体鞘套是指位于激波与再入体之间的等离子体,除等离子体鞘套外,在后方,还会形成范围更广的强度较低的等离子体尾迹。等离子体套鞘使得电磁波传播的功率衰减,且使电磁波产生反射、折射及散射。等离子体鞘套对飞行器与地面站之间的无线电通讯产生极大的影响,影响飞行器的导航制导严重时会造成通讯中断(即黑障)。
本文采用某典型战略导弹头部外形为模型,对再入飞行高度为H =61km,飞行马赫数为11.5即(3621.496m/s),攻角为0度攻角,壁面为完全非催化壁面的情况进行了数值模拟,得到了该模型绕流流场和等离子体的分布情况。
1.控制方程组
高超音速等离子体流场的控制方程组,为具有化学反应源项的Navier-Stokes方程组,包括质量守恒方程、动量守恒方程、总体能量守恒方程和组元相关补充方程。采用数值计算的方式可以得到近似解,但由于高温所引发的分子输送、化学反应、振动激发、辐射等多种非平衡过程的物理化学机理尚未完全掌握,要得到满意的结果模拟结果,必须先由试验确定一些控制参数,如定压比热,化学反应速率等。
控制方程组为四组守恒方程,即质量守恒方程,动量守恒方程,能量守恒方程以及组分质量守恒方程,具体形式见参考文献1
2.高温空气化学反应
2.1 化学反应的分类,
一般情况下化学反应按照反应速率可以分为三类:
2.2 Arrhenius有限化学反应模型
具体模型见参考文献2。 任何不直接参与化学反应但确实由于它的存在影响了反应速率的组分称之为第三体。第三体系数是一个关于反应速率的放大系数,若其值小于 1 表示延迟反应,其值大于 1 表示加速反应。
2.3 再入体化学反应模型
再入体化学反应模型主要有Dunn-Kang模型,由于不同的再入高度和速度,化学反应的组元和反应方程有许多中(见图2)。常见的有5组元、7组元和11组元模型。5组元模型一般用于速度较低无电离的高超声速流动,而7组元和11组元模型常用于计算高超声速非平衡流。
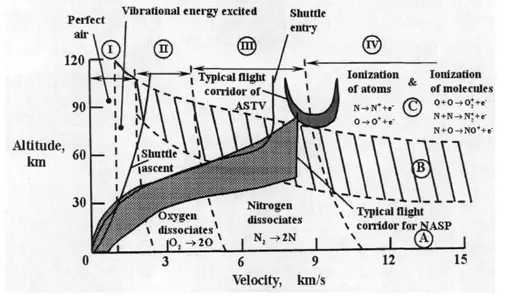
图2 不同速度和高度时再入体化学反应模型
3.定界条件
对于超高音速数值模拟问题来说,仅有上述控制方程组还是不能求解,需要补充定解条件。定解条件包括初始条件和边界条件。
3.1 初始条件
初始条件即计算开始时的流动条件。定常问题,需要从某种初始条件出发,通过迭代,收敛到定常解一般定常解是唯一的,与初始条件无关。假定无穷远处流动为均匀自由流,通常流场计算的初始条件取为自由来流值,进而合理地处理边界条件,就能收敛到定常解。
3.2 边界条件
边界可分为两种:物理边界和人工边界。物理边界是由问题的性质决定的。如固体壁面和进口边界、出口边界都是物理边界。人工边界是针对无限或半无限区域,以及我们感兴趣的范围永远小于实际区域时而人为引入的。边界条件可分为入流边界条件、出流边界条件、远场边界条件、传值边界条件和物面边界条件、奇性轴边界条件等。对于高超声速计算,人工边界和物理边界都存在。压力远场条件为人工边界,取自由来流条件;物面边界为物理边界,需要考虑气动加热和对化学反应催化作用,需要具体问题具体分析。气体与壁面的气动加热是壁面附近气体由于粘性的作用而使得气体动能转换为热能的物理现象。与壁面的温度直接相关,将不出现对流交换时的壁面温度称为绝热温度,壁面对气流加热,则壁面温度必须将高于绝热温度;反之壁面被气流加热。持续受热的特征决定了飞行器在某一时刻的受热环境情况不仅与这一时刻的飞行条件有关,还与这之前飞行器自身热环境所经历的时间历程紧密相关。从气动加热角度来看,高超声速飞行器经历的受热过程是一个持续、非稳态过程。
4.计算模型与结果
4.1 计算模型
某战略导弹头部半径R 为0. 1m ,半锥角12.5°,长度2344.4mm(如图3所示),对应再入飞行高度H =61km ,来流速度均为3621.5m/s(马赫数11.5) , 迎角α= 0°,来流空气由79 %的氮气和21 %的氧气组成,边界条件为模型壁面为绝热壁面,温度为600K,无催化作用,流场边界为压力远场,压力为21.7Pa,温度为247K。化学模型采用7组元7反应的Dunn-Kang模型(见参考文献[1],P243),反应速率遵守Arrhenius 模型,见参考文献[2]。插值格式采用压力权函数修正的迎风型矢通量算法(AUSM格式)。流场如图4所示,13.36m*6m,整个流场网格为结构化的四边形网格组成,网格总数为25.9万,整体网格如图5所示,头部局部网格如图6所示。
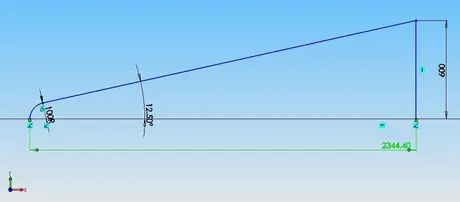
图3 模型尺寸示意图

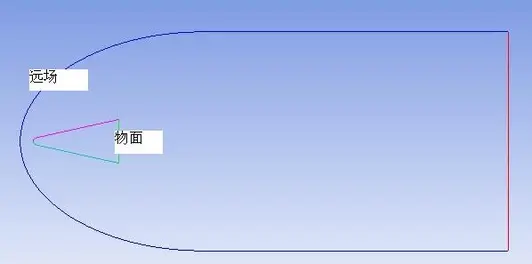
图4 流场示意图


图5 流场网格示意图


图6 模型头部网格示意图
4.2 计算结果
流场压力分布如图7所示,从图中可以看到,弹体的头激波已正确捕捉到。最大压力值为3.78kPa,位于头部驻点处(图8为弹体头部区域的压力分布)。流场的温度分布如图9所示,可以看到,弹体头激波和尾激波都已正确的捕捉到,流场内最大温度为5115.16k,位于头部驻点处,(图10为弹体头部区域的温度分布),图11为整个流场总温的分布云图。图12和图13是流场和弹体头部区域的速度分布云图(以马赫数显示),可以看到和温度分布是一致的。

图7 流场压力示意图

图8 模型头部区域压力示意图
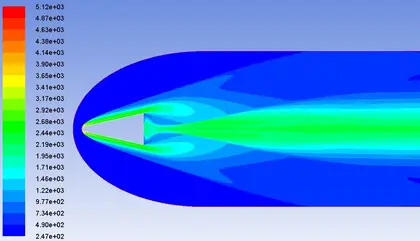
图9 流场温度示意图

图10 模型头部区域温度示意图
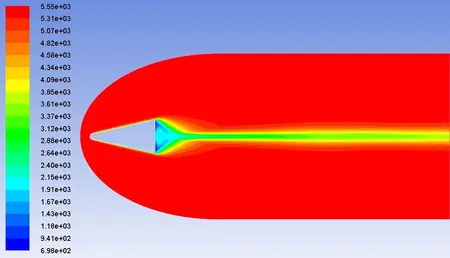
图11 流场总温示意图
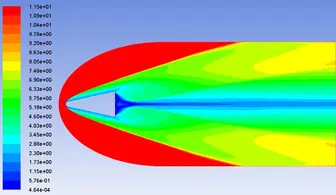
图12 流场速度示意图

图13 模型头部区域速度示意图
图14显示的是轴向各点的电子密度峰值,可以看出头部电子密度比弹体后部高2个数量级,这与参考文献[3]图15是一致的。(由于参考文献马赫数极高为28.3,流场温度也高,所以电子密度也高,本文马赫数为11.5,流场温度较低,模型头部到尾部的电子密度变化趋势和参考文献[3]一致)。
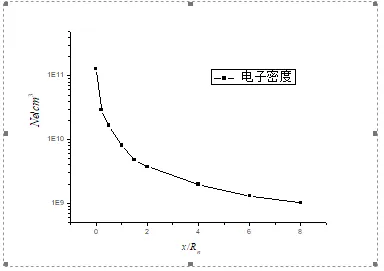
图14 轴向各点电子密度峰值
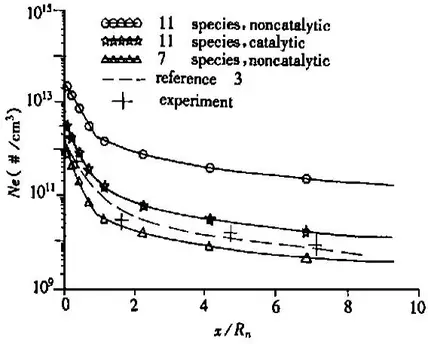
图15 RAM-C轴向各点电子密度峰值
等离子体的计算结果如图16-19所示,图16、18为等值线图,图17、19为云图,显示的是弹体绕流流场的等离子套鞘的电子摩尔组份数(即每摩尔空气中电子所占的比例)。
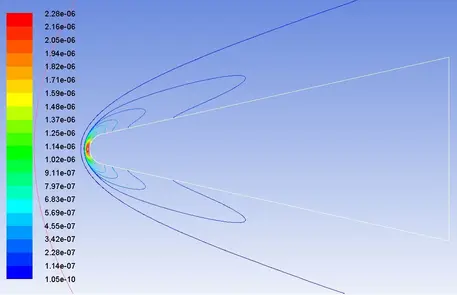
图16 绕流流场电子摩尔组份数等值线图
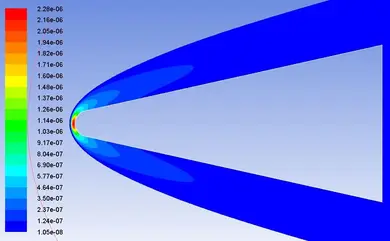
图17 绕流流场电子摩尔组份数云图
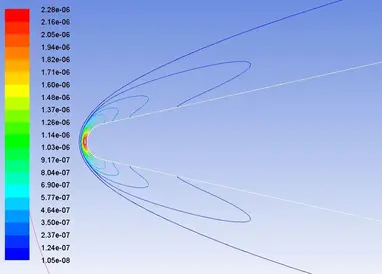
图18 模型头部区域电子摩尔组份数等值线图
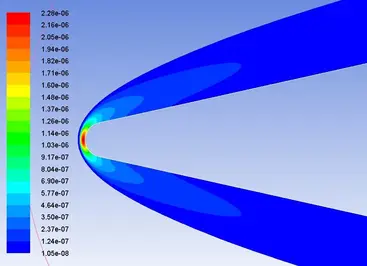
图19 模型头部区域电子摩尔组份数云图
等离子体的电子密度采用空气密度除以空气的摩尔质量29g/mol,得到每立方米的空气分子摩尔数,再乘以电子的摩尔组份数,并乘阿伏加德罗常数(6.02*1023),得到每立方厘米的电子数(电子密度,单位个/cm3)。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删