整车气动模拟新纪元：极大规模数字风洞构建

摘要

本应用基于神威·太湖之光超级计算机与自研自适应加密网格框架（SAMR[1]）完成了某真实汽车模型的气动仿真数值模拟。为提高计算精度与效率，采用了8层网格加密，网格规模约10亿量级、并行规模在50万核并行规模。流场数值求解器则是采用了自主研发的非定常格子玻尔兹曼流场求解器（LBM[2]，Lattice Boltzmann Method）与采用简单的Smagorinsky湍流模型。所计算的Ahmed标准车模阻力系数与实验高度吻合，具备了工程应用能力。

一、背景

在汽车设计和改型中，数值计算和风洞试验是评估气动性能的两大手段。风洞试验模型制作和试验实施的周期长，成本高，因此如何减少风洞实验次数，提高汽车设计效率，一直是汽车设计及空气动力学领域研究的重点。

数字风洞即风洞的数字化，是遵循数字孪生理念，通过高保真数值计算、机器学习等技术手段，将物理风洞试验设施和试验过程1:1还原到数字世界，从而具备实施高置信数字风洞试验的能力。通过数字风洞试验，可以取代部分早期风洞试验车次和部分风洞试验，从而缓解风洞试验成本高、周期长与旺盛试验需求之间的矛盾。

国家超级计算无锡中心神工坊团队，依托我国最先进的国产自主超级计算机神威·太湖之光，自主研制了结构网格自适应框架（SAMR[1]）与格子玻尔兹曼流场求解器（LBM[2],Lattice Boltzmann Method)，形成了自主数值风洞软硬件基础框架，可以高效地为汽车气动仿真赋能。

二、方法

下面对40m/s(或144km/h)速度下的Ahmed标准汽车模型（25°后背角）与某实车模型进行数值模拟。

1）网格生成: 采用国家超级计算无锡中心自主开发的结构网格自适应加密框架，可对汽车中复杂几何表面以及流场变化剧烈的地方进行自动加密。

2）流场求解器:采用国家超级计算无锡中心自主开发的基于多层加密格子玻尔兹曼方法的流场求解器，具有并行效率高且易于处理复杂几何等优点。

3）湍流模型：选用Smagorinsky模型，它是一种简单的大涡模拟模型，且易于在格子玻尔兹曼方法中实现。

三、结果

1）汽车模拟验证

1.1 网格规模：

网格规模6.2亿，采用了8层网格加密。并行规模约13万核（含主核与从核)。注:这里采用6亿网格主要是为了验证大规模计算能力，在小规模网格的算例中我们也得到了与实验基本吻合的阻力系数。

1.2 速度场：

图1 Ahmed车模瞬时速度云图。后背角为25°，来流速度40m/s。

图1中给出了流场完全发展后的速度场瞬态云图，可以看到车模表面进行了更为精细的网格加密。

1.3 阻力系数：

图2 Ahmed车模阻力系数随时间的变化。后背角为25°，来流速度40m/s。

可以看到，我们的计算结果与实验结果吻合的很好。表1给出了我们的阻力系数与Fluent、PowerFlow等商业软件的比较，可以看到我们的计算误差最小。同时也可以看出，PowerFlow与我们的结果明显好于Fluent计算结果，这也间接说明LBM方法在车模计算中是优于FVM方法的。

表1 Ahmed车模阻力系数比较。后背角为25°，来流速度40m/s。

2）实车仿真

2.1 网格规模：

网格规模6.7亿，采用了8层网格加密，其中汽车表面附近做了3层网格加密，能更好的捕捉汽车几何特征以及汽车前后缘的大速度梯度等特征。并行规模约46.8万核（含主核与从核）。

2.2 速度场：

图3 某实车模型瞬时速度云图。来流速度40m/s。

图中给出了流场完全发展后的速度场瞬态云图，可以看到车模表面进行了更为精细的网格加密。

2.3阻力系数：

图4 某实车模型阻力系数随时间的变化。来流速度40m/s。

可以看到，流场完全发展后，某实车模型阻力系数约为0.258。

四、特点

1）结构网格自适应：

网格自适应加密是本应用的主要特点。通过网格自适应，可以对几何外形复杂的区域以及流场变化剧烈的地方着重加密。在我们的结构网格自适应加密框架下，只需要读入汽车几何外形信息，会自动在外形复杂以及流场变化剧烈区域自动加密（如图5自适应网格效果图），在提高计算精度的同时大大节省了人力成本。另外值得一提的是，我们生成的网格是分布式的，这非常适合大规模并行计算。

图5 某车模算例中的网格自适应效果图

2）众核加速二级并行：

本应用的另一个特色是大规模并行效率高。为了适配国产神威太湖之光超级计算机，本数值求解体系从设计之初就融入了主从核异构并行体系，在进行流场数值求解时能充分发挥异构计算机的主核与从核性能。例如，本次汽车模拟算例就采用了7200核组（包含7200*64=46.08万从核）。此外通过测试，发现7200核组相对3600核组，算例获得了几乎翻倍的性能，表明当前的算例大规模并行效率非常的优异。

3）求解器代码精简：

求解器代码精简也是本应用的主要特色。此次求解器采用的LBM流场求解器只涉及几百行代码。由于求解器是基于我们自研的SAMR框架，该框架底层封装了异构并行，对离散层开放了“迭代器+算子”接口，用户只需要设计自己的求解器算子，代入对应的迭代器（空间遍历器）即可完成空间迭代计算。这里算子结构往往十分精简（如图6，复杂的空间遍历与异构并行都被封装到迭代器内部，因而基于这种模式开发的求解器代码往往非常精简易用。）

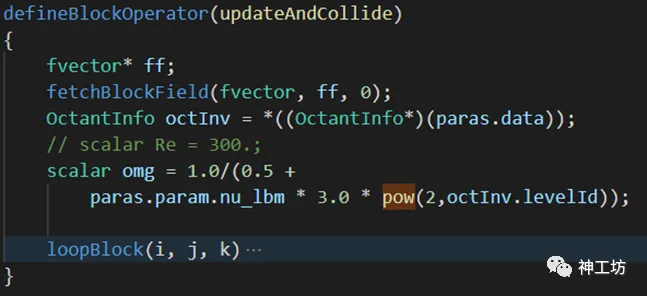
图6 格子玻尔兹曼流场求解器碰撞算子示意图。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删