圣杯问题新解：全纯微分的深度探讨

图1. 波士顿三一教堂（姜健摄）。

2016年感恩节前夕，11月22日，老顾应邀在哈佛大学数学科学中心，既黑洞研究中心，做了一场报告；向丘成桐先生，诸多数学家和物理学家汇报了近期研究成果。许多新朋老友参加了报告会，特别是哈佛大学统计系的刘军教授。报告涵盖了离散曲面里奇流的理论【4】，最优传输问题的凸几何解法【5】，泰西米勒映射的计算方法【6】，以及这些理论方法在工程和医学方面的应用【3】。比如几何数据压缩，医学体数据的虚拟放大镜，动态人脸曲面的表情捕捉等。老顾着重介绍了最近有关圣杯问题的突破【2】：应用全纯二次微分（holomorphic quadratic differentials）诱导曲面叶状结构（surface foliations），进而构造实体（solid）的六面体网格化（hexahedral meshing）。

丘先生对于全纯二次微分计算方法的突破倍感欣慰，其实丘先生早在十五年前就要求老顾探索这一方向。那时的老顾知识储备不够，对于共形几何的理解不够透彻，理论功力和工程技巧不足以解决这个基本问题。更大的原因在于当时无法看清这一理论的实际应用前景，因而缺乏由衷的动力。虽然理论上全纯二次微分在整个共形几何中起到了支柱性的作用，但是在工程领域没有任何人提出这一理论可能的应用前景。当时，老顾也不知道圣杯问题的确切提法，更无法想象圣杯问题和全纯二次微分之间迂回曲折，却又至关重要的内在联系。但是丘先生一再坚持让老顾加强这方面的理论修养，同时亲自在哈佛数学系开课讲授曲面叶状结构理论，瑟斯顿（Thurston）的Teichmuller空间紧化理论，和McMullen运用叶状结构研究动态系统的理论。多年之后，老顾终于意识到这些理论对于实际工程问题的指导作用，对于丘先生的高瞻远瞩无比钦佩。

全纯一形式

2001年左右，依随图形处理器GPU (Graphics Processing Unit)技术的兴起，纹理贴图（Texture Mapping）技术极大地提高了动画渲染的质量。纹理贴图技术依赖于所谓的曲面参数化(Surface Parameterization)技术，亦即寻求曲面到平面区域的映射，要求此映射是微分同胚，同时尽量减小映射带来的畸变。在计算机图形学领域中，许多学者开始尝试用共形映射（conformal mapping）来解决曲面参数化问题。当时人们只能计算拓扑圆盘到平面区域间的共形映射，例如经典的黎曼映照，即所谓的局部参数化方法。所谓的全局参数化，即计算拓扑复杂曲面间的共形映射成为万众瞩目的核心问题。

丘先生指导老顾一举解决了这一问题，其方法的核心就是全纯一次微分（holomorphic One Form）【1】。全纯微分是黎曼面理论中的核心概念，其定义佶屈聱牙，隐晦抽象，很难令初学者领悟，也很难向别人传达精神实质。在日常生活经验中，并没有显而易见的范例。历史上，这一概念只存在于数学家头脑之中，没有任何人真实地看到过拓扑复杂曲面上的全纯一形式。对于数学家如何发现这一深刻的几何概念，令人大惑不解，对于人类智慧能够到达的深邃程度，当时的老顾只有惊叹。

丘先生指导老顾做出的算法使得全纯一形式这一神秘概念变得随意可算，平易近人。通过可视化技术，人们可以直接看到这一抽象概念，从而轻而易举地建立直觉。全纯一形式提供了计算曲面间共形映射的强有力方法。后来，众多合作者们将这一方法打磨提炼，拓展推广，逐步向许多工程和医疗领域渗透。十数年后，这种方法已在工业界和医疗界被广泛采用，西门子，通用电气，MathWorks，暴雪等很多公司都采用了全纯一次微分的算法，应用于癌症诊断，科学计算和动漫动画等实际问题。

图2. 亏格为二的曲面上，调和一形式群的基底。

我们先从物理角度入手来理解全纯一形式。考察空间中在远离电荷处的静电场，电场强度是一个矢量场。如果我们将一个带电粒子沿着一条封闭曲线移动一周，则电场对带电粒子所做的总功为零，粒子的电势不发生改变。这意味着矢量场的旋量处处为零。同时因为矢量场内部没有电荷，因此散度处处为零。旋量和散度处处为零的矢量场被称为是调和场（Harmonic Forms）。

调和场对加法和数乘运算封闭，因此曲面上所有的调和场构成线性空间。霍奇定理（Hodge Theory）断言，调和场构成的线性空间，或者阿贝尔群，和曲面的上同调群同构。调和场满足椭圆型偏微分方程，上同调群是拓扑结构，因此霍奇定理连接了分析和拓扑两大领域，其自然推广是指标定理。图2显示了一个亏格为二的曲面上，调和场所构成的群的基底。

图3. 亏格为二的曲面上全纯一形式的基底。

给定曲面上的一个调和场，我们将切矢量逐点围绕法向量旋转90度，得到的另外一个矢量场也是调和场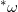，这里*被称为霍奇星算子，代表旋转90度的操作。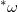称之为是的共轭调和场。我们将一对共轭的实调和场配对，得到复的全纯一形式。

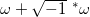图4. 亏格为一的曲面上的全纯一形式。

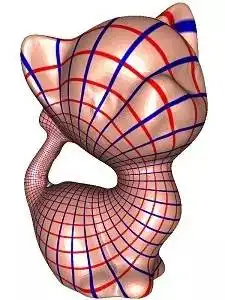
图5. 全纯一形式诱导的水平和铅直轨线。

共形映射 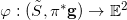平面上的水平线和铅直线拉回到曲面上，得到所谓的水平轨迹和铅直轨迹，如图5所示。

图6. 黎曼面。

经典的教科书定义全纯一形式如下。给定带度量的可定向曲面，对于任意一点，存在一个包含该点的邻域，在此邻域上存在所谓的等温坐标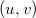（isothermal parameters），使得黎曼度量的局部表示为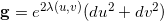。我们可以用等温坐标构成整个曲面的图册，如图6所示，那么所有局部坐标之间的变换函数都是复数值的全纯函数（holomorphic function）。这样的图册被称为是共形图册，具有共形图册的曲面被称为是黎曼面。有了共形图册，角度可以被定义。通常，共形图册也被称为是共形结构。

全纯二次微分

图7.全纯一形式的轨线和全纯二次微分的轨线对比。

图7显示了全纯一形式的轨线和全纯二次微分轨线的对比，我们看到在正常点附近，两者区别不大；单是在零点附近，两者性状差异较大。全纯一形式的零点是8个方格粘在一起，全纯二次微分的零点是6个方格贴在一起。实际上，全纯一形式整体平方后也是全纯二次微分，因此全纯二次微分是全纯一形式的自然推广。

 图8. 共形映射和拟共形映射对比。

全纯二次微分在拟共形映射(Quasi-Conformal Map)和泰西米勒理论(Teichmuller Theory)中起到了核心作用。共形映射将源曲面上无穷小圆映成目标曲面上的无穷小圆，如图8上面一行所示；拟共形映射将无穷小椭圆映成无穷小圆，如图8下面一行所示。

图9. 带有特征点的拓扑圆盘曲面间，一般不存在共形映射。

叶状结构

图10. 亏格为3的曲面上的叶状结构。

全纯二次微分的水平轨迹构成了曲面的一个叶状结构（Foliation），同样的，其铅直轨迹也构成了曲面的另一个叶状结构。所谓叶状结构就是将曲面分解为曲线的并集，每一条曲线被称为是一片叶子。每片叶子没有自相交，任意两片叶子没有交点。局部上看，相差一个微分同胚，叶子们彼此平行。每片叶子有可能是有限的圆，也有可能是无限的螺旋线。如果一个叶状结构的所有叶子都是有限圆，则这一叶状结构被称为是有限的。

未来展望

当晚，丘先生在麻省理工附近的五月花餐馆宴请大家，龙虾石斑，牛蛙刀蚬，异常丰盛，足见丘先生的欣慰之情。席间，丘先生郑重叮嘱老顾团队：“全纯二次微分对于共形结构的模空间至关重要；下一步，我们应该探索高阶全纯微分的计算方法，以及射影结构的模空间。”

一句话再度令老顾血脉贲张，为未来十年指明了努力方向。虽然目前没有人能够看出射影结构模空间的实际应用前景，但是老顾相信历史会再度重演。只要我们能够算出大自然内在几何结构的一部分，那么迟早人类的技术能够追赶上来，使得这一结构在实际领域中发挥根本的作用！

感恩

一年来的奔波劳顿，使得心灵又磨出一层老茧。感恩节降临，终于有时间和灵魂独处，内心也变得些许柔软。回顾十数年来的求索历程，宛若一名孤独的朝圣者，跋涉在优胜美地，虽然历尽艰辛，但是领略了大自然的雄奇壮丽。从数百年前黎曼开创的黎曼面理论，到阿尔福斯创立的拟共形几何理论，再到泰西米勒发展的泰西米勒空间理论，直至Strebel的全纯微分理论，一路走来，领悟了历史上许多大师的深邃哲思，既到达过人迹罕至的原始山林，也直面过峥嵘万仞的绝壁。为了将这些精美绝伦的抽象数学转化为平易近人的算法程序，只是追随前人数学家的足迹是远远不够的，绝大多数的时候需要辗转腾挪，独辟蹊径。生活的常态就是经年累月的殚精竭虑，冥思苦想。在抵御外在物质世界诱惑的同时，更为困难的是抵抗自身犹疑畏惧，轻言放弃的心魔。这种精神上的苦修，如人饮水，冷暖自知。当看到一个个以前只能用思想触及的几何结构，渐渐可以用计算机程序来把握，一个个数学定理渐渐融入计算机科学，那种精神上的满足，无法用语言来形容。

这条朝圣之路非常艰辛，这种苦修的学术之路和当代社会盛行的价值观念背道而驰。首先这需要纯粹数学和计算机科学两方面的知识结构，理论证明和工程实现两种不同的技巧，因此需要更长时间的学习和磨炼，而这是以青春为代价。其次，目前在学术标准日益被商业准则同化的氛围下，理论的深刻性和严格性让位于含混唯像的实用性。在过去，我们花了两年提出了高效的算法，却花了五六年来证明这一算法的严格性，这在当今工程领域被视为是保守迂腐的做派。特别是目前青年学者的生存压力空前巨大，在浮躁高压体制下花费五六年来完善一套理论无异于学术自杀。很难想象会有年轻人为了美学价值而置身家性命于不顾，为了科学的纯洁崇高而主动殉道。对于青年学生而言，研习抽象深刻的几何理论无异于学习屠龙之术，青春耗尽而市场并无需求。相反的，有人只学习了表象的算法，虽然知其然却不知其所以然，却可以迅速创业，融资千万。更有很多学者学生，苦心孤诣，不懈求索，但却不被人理解。尤其是朋友家人用世俗的观念来衡量他们付出的心血，埋怨责骂，嘲笑讥讽。在强大的世俗压力下面，他们承受着难以想象的折磨和愤懑。这一切，每天都在老顾身边的朋友中发生。

在过去的一年中，依然有许多学者学生认同老顾的理念，主动和老顾合作，与老顾一同不改初衷，苦苦求索。更有很多长辈师长，对于老顾的研究工作大力支持，无私帮助。对于这些志同道合的师长和朋友，老顾诚挚地感激他们的学术支持，更由衷地敬佩他们的人格力量。对于那些依然在苦苦支撑的青年学者学生，老顾相信他们艰苦卓绝后终成大器。沧海横流，方显英雄本色！

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删