根据提供的卡扣几何模型、材料数据、载荷数据,对其进行卡扣滑动计算。采用ANSYS建立卡扣的有限元模型并施加载荷,获得卡扣的滑动力曲线。
关键字:ANSYS;非线性接触;卡扣;滑动力;
1 问题来源与分析目的
根据提供的卡扣与导轨几何模型、材料数据、载荷数据,对其进行卡扣滑动计算。采用ANSYS建立卡扣的有限元模型并施加载荷,获得卡扣滑动时的滑动力的大小。

图1 卡扣与导轨的实际模型

图2 计算目的
本次分析模型由微软某中心提供,如下图所示。根据分析目的和模型特点,可以采用二分之一模型,并根据边界处理条件对模型进行一定的简化,以达到减少计算规模的目的
根据分析目的,需要获取卡扣滑动时的滑动力大小,直接进行滑动力的施加,不容易得到准确的计算结果,而且对计算过程中的数值稳定性有一定的影响,所以将载荷加载改为位移加载,提取支反力大小,最终确定滑动力与滑动距离的关系,获得最终的计算结果。实际约束和加载如下图所示,导轨(蓝**域)底面进行固定约束,卡扣尾端(红**域)施加位移载荷,大小为11mm。
整个计算过程中所采用的单位系统为:长度-毫米(mm);质量-吨(t);力-牛顿(N);时间-秒(sec);导出单位:密度-吨/毫米3 ( t/ mm3);弹性模量-牛/毫米2 (N/mm2),即MPa;应力-牛/毫米2 (N/mm2) ,即MPa。
卡扣和导轨的材料(Ticona)参数如下表所示
表1 材料力学参数
| 材料名称 | 弹性模量(Gpa) | 泊松比 | 屈服极限(Mpa) |
| 摇臂 | 15 | 0.35 | 12 |
由于卡扣在滑动过程中会发生较大变形,并产生较大的应力,会发生塑性变形,所以需要输入塑性区域的材料参数,采用各向同性的多线性材料本构,输入其应力应变曲线,如下图所示:
图6 材料的应力应变曲线
表2 塑性区域的应力—应变数据
| 应变 | 0 | 1e-3 | 4e-3 | 5e-3 | 6e-3 | 8e-3 | 1.6e-2 |
| 应力(Mpa) | 12 | 46 | 136 | 149 | 154 | 158 | 162 |
根据模型的结构特点,生成高质量的网格。选择不同单元类型进行网格划分:由于卡扣在滑动过程中会与导轨相互挤压,导致网格的扭曲变形,所以需要对接触区域进行六面体(Solid186)网格划分,其他区域进行四面体(Solid187)网格划分,导轨其他部分为不关心区域,所以采用较粗网格,卡扣区域需要得到较好的应力结果,所以采用四面体网格加密,总体单元数为66557个,节点数为112923个。最终形成的整体有限元计算模型如下图所示:

图7 有限元模型
对于卡扣与导轨之间的接触关系处理是本次分析的重点,根据实验获得的摩擦系数,导轨与卡扣之间的摩擦系数为0.2,导轨为目标面(蓝色),卡扣为接触面(红色),接触算法为Augmented Lagrange算法,罚刚度因子为0.2。

图8 接触设置
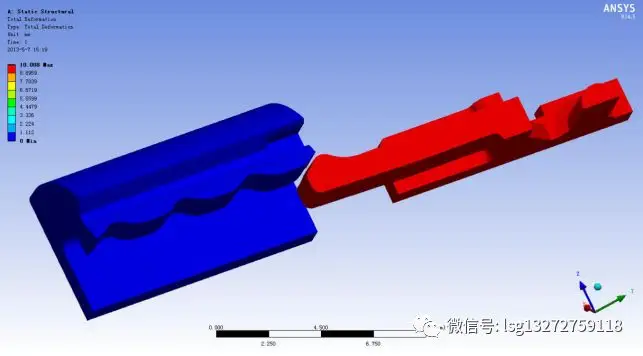
图9 计算完成后的卡扣位置
图10 卡扣滑动后产生的残余应力
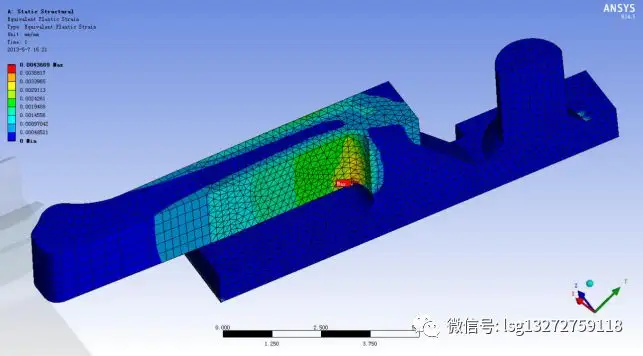
图11 卡扣滑动后产生的塑性变形
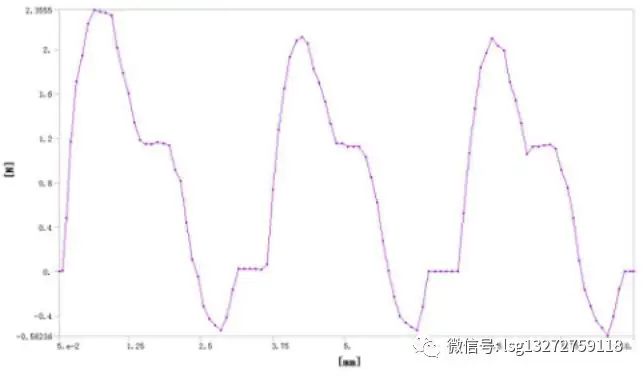
图12 卡扣滑动位移与滑动力的变化曲线
根据上述计算结果可知,卡扣在初始滑动中的最大滑动力为4.7N,因为采用的是1/2模型,所以在原有数值上需要乘以2。后续滑动需要的滑动力为4.2N,原因是卡扣发生了较小的塑性变形,产生了不可恢复的变形。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删