网格划分差异解析：专家观点汇总

前言

有限元网格划分是有限元分析前处理的重要环节，有限元单元类型的选择、单元尺寸大小控制、网格划分方式都对分析结果的准确性有很大影响。不同的分析人员网格划分的结果都不一样，这也直接导致应力分析的结果不唯一。

有限元网格概述

对于结构有限元应力分析，最常用的是四面体网格和六面体网格。在ANSYS中的四面体推荐使用10节点高阶的Solid187单元，该单元具有一下特点：

1) 产生网格容易；

2) 对模型的适应性强；

3) 基于四面体单元可以进行自适应网格加密。

如图1给出了四面体187单元的示意图，该单元为ANSYS单元库中的10节点高阶四面体单元，也是ANSYS Workbench环境中对复杂模型优先使用的单元。

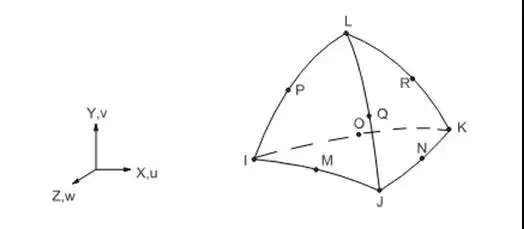
图2给出了四面体Solid285单元的示意图，该单元为ANSYS单元库中的4节点低阶四面体单元。

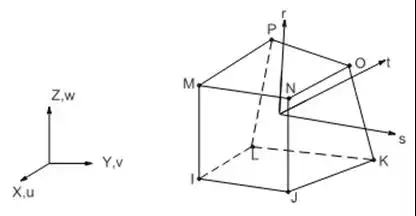
在ANSYS中高阶六面体结构单元就是Solid186单元，如图3所示，六面体单元的特点：

1) 适合简单模型进行网格划分；

2) 对于复杂模型，需要在前处理耗费较长时间，对复杂模型的适应性差；

图4给出了六面体Solid185单元的示意图，该单元为ANSYS单元库中的8节点低阶六面体单元。

不同行业专家的观点

总体来说，对于空间物体而言，我们应当尽量使用六面体网格。

当对象是一个简单的规则体时，使用扫掠网格划分是合适的；当对象是多个简单的规则体组成时，使用多域扫掠网格划分是合适的；接着尽量使用六面体主导的方式，它会在外层形成六面体网格，而在心部填充四面体网格。

四面体网格是最后的选择。其中如果要忽略一些小细节，如倒角，小孔等，则使用patch independent算法;如果要要考虑一些小细节，则使用patch conforming算法。至于自动网格划分，是最傻瓜化的方式，一般对于初学者适用。

Fangzhenxiu专栏作者张老师在“ANSYS空间”发表的文章《四面体单元与六面体单元的选择建议》中给大家的使用建议：

1) 如果使用自动方法不能产生六面体单元的模型，建议使用四面体；

2) 通过提升四面体单元的密度，来提升计算精度，这样处理可以大大减少模型前处理的时间，来实现仿真的时效性优势，关于计算精度对比，后面会通过实例进行对比。

另外，在《ANSYS有限元网格划分的基本原则》一文中写道：单元质量评价一般可采用以下几个指标：

1) 单元的边长比、面积比或体积比以正三角形、正四面体、正六面体为参考基准。理想单元的边长比为1，可接受单元的边长比的范围线性单元长宽比小于3，二次单元小于10。对于同形态的单元，线性单元对边长比的敏感性较高阶单元高，非线性比线性分析更敏感。

2) 扭曲度：单元面内的扭转和面外的翘曲程度。

3) 疏密过渡：网格的疏密主要表现为应力梯度方向和横向过渡情况，应力集中的情况应妥善处理，而对于分析影响较小的局部特征应分析其情况，如外圆角的影响比内圆角的影响小的多。

4) 节点编号排布：节点编号对于求解过程中的总体刚度矩阵的元素分布、分析耗时、内存及空间有一定的影响。合理的节点、单元编号有助于利用刚度矩阵对称、带状分布、稀疏矩阵等方法提高求解效率，同时要注意消除重复的节点和单元。

不良的单元形状会导致不准确的结果，然而到目前为止，还没有一个比较通用的标准来判定单元形状的好坏。一种单元形状在一个分析中可能会带来不正确的结果，但在另外一个分析中又可能是完全能接受的，因而单元形状的好坏以及结果的准确性完全由用户根据经验或者相关行业规范进行判定和分析。所以平时我们在采用ANSYS进行有限元分析时，一个很重要的步骤便是查看网格质量，有时即使网格划分成功了，若质量太差，结果也不一定具有可信性，故而好的网格质量是保证分析结果精确的首要条件。

其总结的网格质量评价指标如下：

1) Aspect Radio（网格纵横比）：其值越接近1，说明网格质量越好。

2) Parallel Deviation（对边偏角差）：其值越接近0，说明网格质量越好。

3) Maximum Corner Angle（单元最大内角）：三角形，越接近60度越好；四边形，越接近90度越好。

4) Jacobian Ratio（雅克比比率）：其值越接近1，说明网格质量越好。

5) Wraping Factor（翘曲系数）：其值越接近0，说明网格质量越好。

6) Element Quality（网格质量系数）：其值越接近1，说明网格质量越好。

7) Skewness（偏斜系数）：其值越接近0，说明网格质量越好。

8) Orthogonal Quality（正交质量系数）：其值越接近1，说明网格质量越好。

有时想要划分出六面体，却怎么也实现不了，一部分是六面体，一部分却只能是四面体，不敢给外人展示，好尴尬。报告里面如果给出漂漂的六面体网格，那是计算结果真实准确的体现，客户也会相信你的计算结果。网格质量的好坏是计算结果能否被接受的重要因素，如果网格质量很粗糙，那么这个计算很可能被否掉，直接拉回去毙了。

我们做了很多整体分析设计，网格划分质量99%都是六面体，只有一个或两个体实在是无法划分出六面体，就像钻石的纯净度一样，只有很少很少的污点，瑕不掩玉。

对于有些结构很难划分出六面体，常常会出现很奇葩的问题，比如体上的线都是断的，让划分网格变得很困难，自由划分也不行，多区域划分也不行，扫略更不行了，弄了一上午都划分不出来，哦，疯掉的感觉。

陆明万、徐鸿在论文《分析设计中若干重要问题的讨论》中对压力容器分析设计网格划分提出一下建议：

1) 板壳结构采用实体单元进行模拟时，厚度方向应有4层线性单元或2层二次单元。

2) 1/4圆弧一般分为6~8个单元。

3) 四边形单元的长宽比一般在1:1到1:3之间。在板壳结构中，均匀的薄膜应力和弯曲应力区可以取1:5~7，最多可以放大到1:10。

4) 三角形单元的锐角一般不小于30°，最小到15°。四边形单元的最小夹角一般不小于45°。

5) 应力梯度大的地方网格要加密。在主要的递减（或递增）区间内至少3~4个单元。

6) 疏密网格的尺寸比一般不大于2。

7) 对尚无经验的算例，需要论证网格尺寸大小的合理性。做基本网格和尺度加密1倍的网格两个算例，若两者计算结果只差在3%~5%以下，则基本网格是可用的。

在北京希格玛仿真技术有限公司发布的压力容器局部开发应力分析软件NSAS：选择高阶单元时，厚度方向2层，选择低阶单元时，厚度方向4层，均采用六面体单元。

ANSYS软件网格质量评判指标

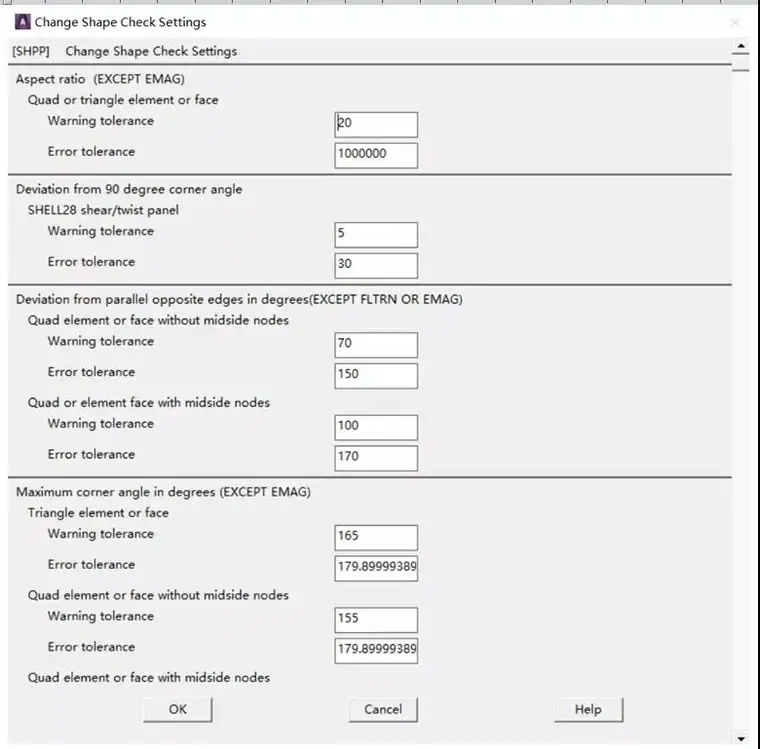
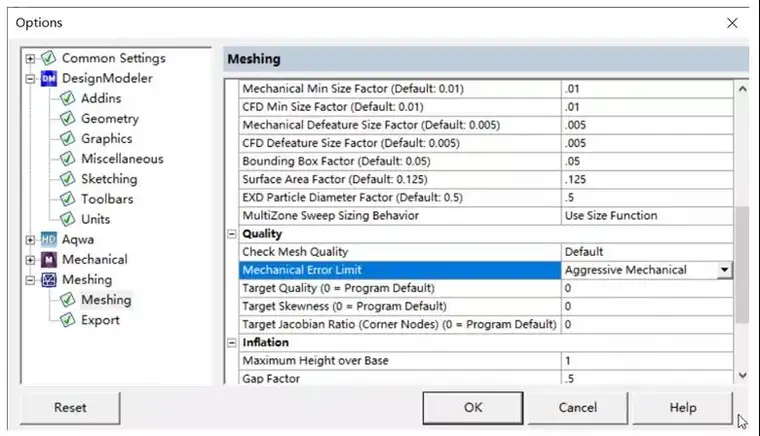
ANSYS经典中单元形状检查默认设置如下。

ANSYS Workbench

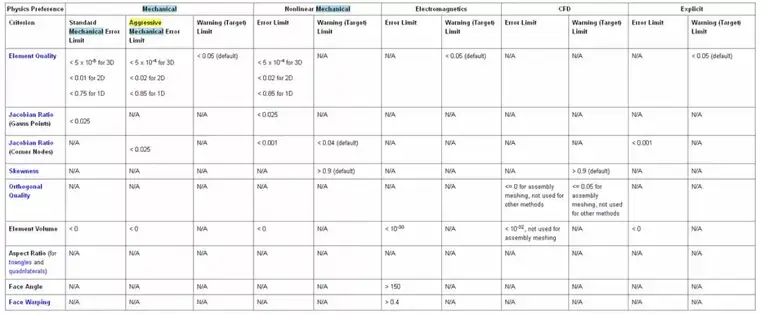
ANSYS Workbench中单元质量评价指标如下，其类别和含义即为前文中所描述。

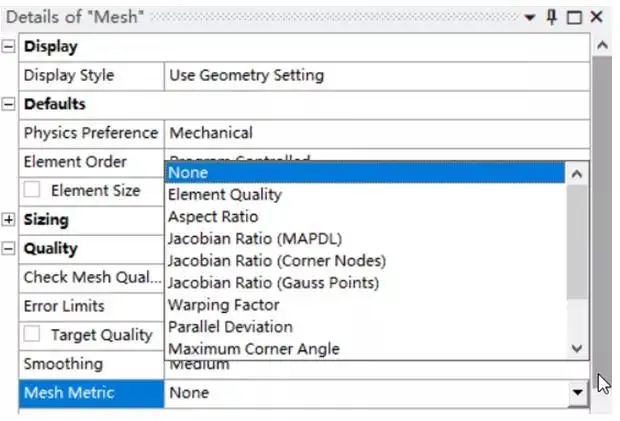
默认的限制值如下（来源于ANSYS帮助文件）。

Workbench中增加了单元质量显示功能，如下图所示，能看到对应质量单元的数量及分布位置。

各规范对网格的要求

GB/T33582-2017

GB/T33582-2017《机械产品结构有限元力学分析通用规则》对于7.4条网格划分要求如下：对于实体单元网格，在结构厚度方向上应确保三层以上。

另外在附录B.3中提出网格控制指标如下：

SYT7403-2018

SYT7403-2018《油气输送管道应变设计规范》对于管道有限元应力分析单元尺寸的要求主要有以下两点：

1) 当采用管单元时，直线段单元划分的长度不宜大于管径。弯管段单元划分长度不宜大于0.5倍管径且划分节点数不应小于3个；

2) 当采用壳单元时，应根据管道各部分变形特点进行网格划分，包括单元密度、大小和形状。划分的单元边长不宜大于0.3倍管径。

BS7910-2013

BS7910-2013《Guide to methods for assessing the acceptability of flaws in metallic structures》在对管道局部腐蚀减薄分析计算程序中，给出了建模、单元及网格的要求。G.9.4 网格设计相关内容及对应中文翻译如下：

单元类型应该适合正在进行的分析。三维连续单元优于壳单元，应使用二阶、二十个节点的缩减积分六面体单元。应该避免严重的单元变形，特别是在 LTA 的最小韧带处。如果使用壳单元，它们应在公式中包括可变壁厚，并允许截面偏移以表示 LTA 处的内部或外部材料损失。整个厚度至少应使用 11 个积分点。（5层高阶单元）

DNV GL RP C208-2016

DNV GL RP C208-2016《Determination of structural capacity by non-linear finite element analysis methods》对有限元网格要求做了比较详细规定，主要条款对应原文和中文翻译如下：

1) 一般来说，焊接在一起的的结构件应该采用连续网格进行网格划分。

2) 除非验证了应力和应变结果的准确性，并在评估结果时对其进行了说明，否则相关区域的焊接细节不应使用粘结接触或运动耦合等连接。

3) 单元类型和公式的选择与分析问题密切相关。

要考虑的项目是：

• 壳单元或实体单元
• 基于常数、线性或高阶形状函数的元素
• 完全vs缩减，v. 混合积分公式
• 贯穿厚度积分点的数量（壳）
• 体积锁定、膜锁定和横向剪切锁定

推荐做法

• 沙漏控制/人工应变能（用于缩减积分单元）
• 旋转刚度/人工应变能（对于壳单元）。
• 翘曲刚度（壳单元）。

4) 一般来说，精确应力估计应该首选高阶单元；如果采用低阶单元，将需要更多数量的单元才能达到高阶单元相同的应力精度。不建议在感兴趣的区域使用低阶应力单元。

5) 对于大位移和大旋转分析，与高阶单元相比，低阶单元提供了更稳健的数值模型和分析。

6) 某些类型的单元用作过渡单元，以便更容易生成网格，尽管已知其性能较差。通常，三节点板/壳和四节点四面体通常用作过渡单元。如有可能，应避免在感兴趣的区域使用这些类型的单元。

7) 如果在同一模型中使用了不同阶的单元，则应确保相邻单元之间的适当连续性。

8) 单元网格应足够详细，以捕获相关失效模式：

• 对于韧性评估，最好在屈服区中存在几个单元，以便进行良好的应变估计。
• 对于稳定性评估，应使用足够数量的单元和自由度来捕获相关屈曲模式，通常应根据每个预期半波的单元类型至少使用3到6个单元。
• 单元纵横比应符合感兴趣区域内选定单元算法的要求。通常，在变形较大的区域及其附近需要接近1的纵横比。
• 在网格密度过渡时需要小心，差异太大会引入数值性质的错误。
• 载荷分布和载荷类型也会对网格密度产生影响。施加荷载的节点需要正确定位，在这种情况下，可以至少在局部修改网格设计。

9) 通常有必要进行网格敏感性研究，以验证分析结果是否足够准确。分析员应确保单元网格足以表示所有相关故障模式。在一般情况下，可以通过检查结果是否收敛来进行网格细化研究，例如，通过使用一半的单元大小重新运行分析来证明结果是合理稳定的。请注意，几何尖角表示永远无法收敛的奇点。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删