ANSYS Mechanical 2022 R1新功能揭秘：模态综合法(CMS)

通过两个不同的音叉本体及相同的音叉把手子结构，讲述了如何在Ansys Workbench中快速完成基于模态综合法的动力学分析。2022 R1中的这个新功能比起传统在经典界面下的操作，要方便很多，这为大规模动力学计算提供了更加便利快速的方法。

传统有限元方法求解结构动力问题，面对复杂大型结构进行求解时，通常存在下列问题：网格数量大、计算时间长、高度依赖计算机资源。例如飞机、车辆、船舶、高层建筑、工程机械等结构通常模型规模宏大，为了获取较准确模态参数，往往要求结构划分较多单元，直接求解耗费大量资源，效率低下。

模态综合法（Component Mode Synthesis）就是在这样的背景下发展起来的一种缩减自由度方法。通过将复杂模型分解成若干个较简单的子结构，对每个子结构分别进行模态分析，然后通过一定的模型组装规则进行模态综合。所谓综合指的是将彼此分开独立的结构组合成一个整体，综合过程中需要满足各个子结构间的兼容性和平衡约束条件。

Ansys中采用三步法处理模态综合问题：1、超单元的生成(Generation pass)；2、超单元的使用(Use pass)；3、超单元的扩展(Expansion pass)。

以往在Ansys经典界面下，完成CMS三步法有着严格的操作步骤，其过程极其繁琐。如今在Ansys Workbench 2022 R1中新增了Substructure Generation功能，我们可以通过Workbench便捷性的操作，快速完成基于模态综合法的动力学分析。接下来我们以音叉结构自由模态分析为例，具体讲述如何通过Workbench平台建立模态综合完成模态分析。

音叉结构分为两部分，上部Y型结构为音叉本体，下部结构为把手（见图1）。为了作对比测试，我们同时进行完整模型的自由模态分析。

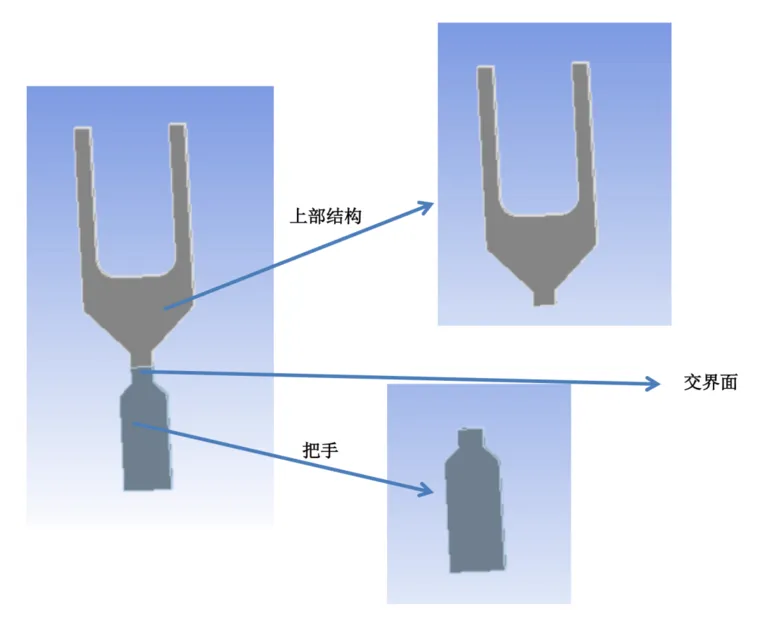
图1：音叉结构示意

我们将把手部位作为子结构，上部结构作为非子结构。

操作过程如下：

1、拖入Substructure Generation模块，搭建把手超单元生成过程。

2、进入model。将把手与上部结构交界面上的节点建立named selection，命名为n。

3、在Substructure Definition内选择相应几何作为子结构本体（本例就是把手部件），在worksheet内插入刚才建立的n，定义主节点。然后右键generate，生成超单元。（图2）

4、设置超单元内固定界面法模态分析阶数，本例为6，完成模型缩聚求解。

5、求解完成后，可以得到子结构固有频率及振型（图3），并且可以导出以.cpa为后缀的超单元文件（图4），本例命名为handle.cpa。

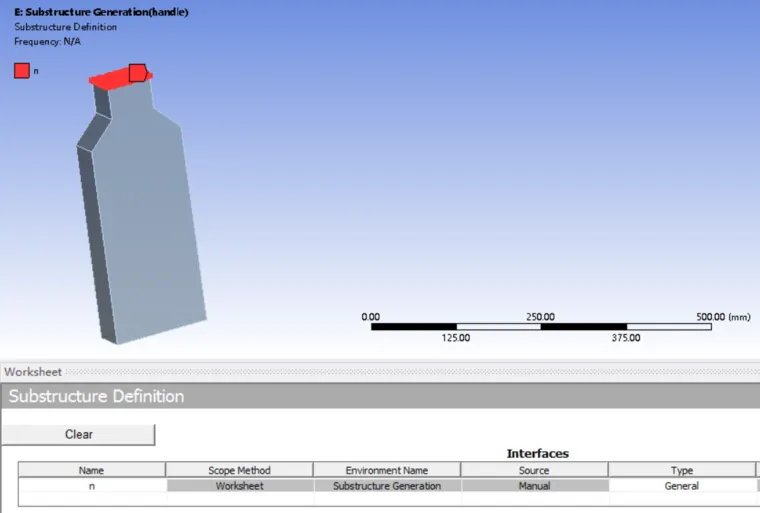
图2：使用named selection方式定义主节点

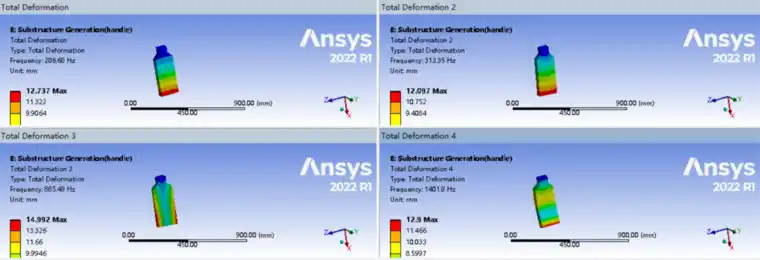
图3：前四阶子结构固有频率及振型

图4：导出CPA文件

通过上述步骤，我们完成了超单元的建立，并导出了超单元CPA文件。该文件就像CAD里的块，可以反复调用。接下来我们以相同的音叉把手作为“块”，分析不同的音叉本体（长音叉、短音叉）的模态。

1、完成长音叉（除把手外）的网格划分、即完成非超单元的网格划分。（图5）

2、右键model>Condense Geometry。

3、右键Condense Geometry>Imported condensed part，导入外部超单元。

4、从Condensed Part file路径中选择之前生成的超单元Handle.cpa。（图6）。可以发现程序自动进行了节点偏移。此时主界面生成了所有结构，其中超单元部分以红色线框表示。（图7）

5、在完成常规模态分析之前，还有一步很重要的工作要做，就是定义超单元与非超单元之间的连接，此处我们采用耦合自由度的方式完成连接。在Modal界面插入Command，输入如下命令流：cpintf,all ，即耦合交界面上所有自由度。

6、完成模态分析，提取前六阶非零模态。见表1。

图5：非超单元网格划分

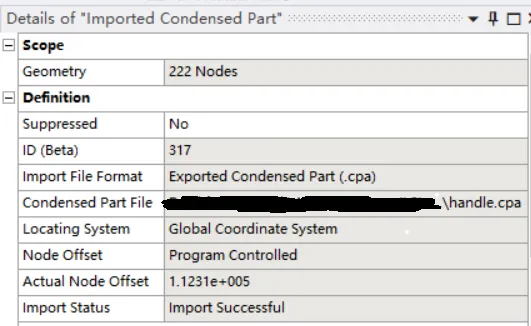
图6：导入外部cpa文件

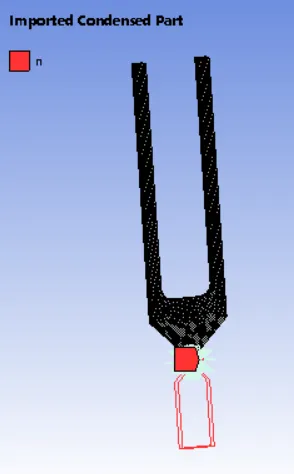
图7：长音叉整体结构（红色线框为超单元）

表1：长音叉前六阶非零固有频率(Hz)（CMS法）

重复上述步骤1~6，我们可以完成短音叉的网格划分，超单元的导入和组装，耦合界面自由度，模态分析等（图8），得到短音叉基于CMS法的前六阶非零固有频率，见表2。

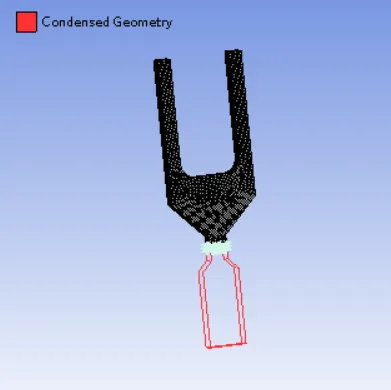
图8：短音叉的整体结构（红色线框为超单元）

表2：短音叉前六阶非零固有频率(Hz)（CMS法）

从前文可以看到，通过CMS法可以很方便地完成子结构的生成，子结构的导入并完成相应的动力学分析。为了进一步验证CMS的计算效率和精度，我们同时做了长音叉结构和短音叉结构全模型的模态分析，提取了前12阶非零模态，统计了计算时间，得到对比结果见表3。

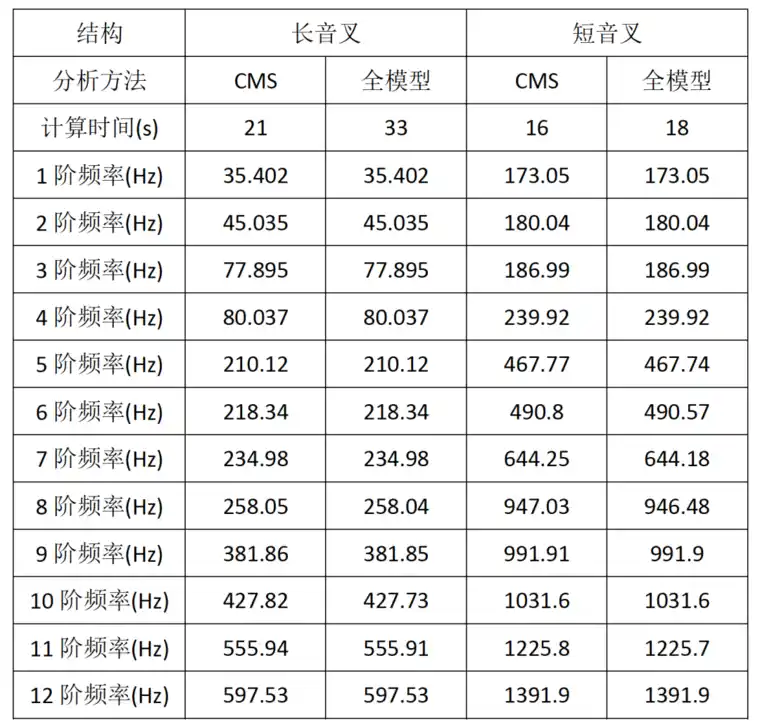
表3：音叉结构基于CMS和全模型前12阶非零固有频率结果对比

从表3的结果，我们可以得到如下结论：

1、采用CMS进行模态分析，在低频阶段几乎与全模型完全一致，仅仅在高频阶段与全模型略有差异，且误差非常小。

2、从求解时间上看，采用CMS法可以缩短求解时间。虽然长音叉的非子结构部分单元数明显大于短音叉非子结构部分单元数，但是长音叉模型的计算时间的节省量却大于短音叉模型的计算时间节省量，这是因为长音叉结构提取的固有频率比短音叉结构偏低，CMS在分析低频结构上会更有效率，这是模态综合法特有的优势。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删