计算机辅助工程,简称CAE,对于经验丰富的CAE分析工程师或学者而言,结合功能强大的CAE程序,大多数结构的数值模拟分析基本上可以做到仿真的地步。现代大型CAE分析程序,如ABAQUS,ADINA,ANSYS,MARC等,无论在荷载条件的输入、边界条件的设置以及非线性算法的准确性上基本已经做到精确模拟的程度,甚至连很多参数性试验都已经可以通过计算机模拟来代替。

近几年,大型CAE分析程序均已渗入传统设计行业,提高了工程设计水平,但纯粹的有限元分析并不等同于结构设计,将结构设计的一些重要参数和概念引入通用分析过程,实现分析与设计的统一,才是使用通用程序进行工程分析的关键之处。本文旨在结合这些程序在工程设计中使用的一些经验进行总结探讨。
1 大型商用程序的一般技术特征
大型通用分析程序起源于20世纪70年代有限元分析方法的建立,在20世纪70年代末和80年代初,一批功能强大的有限元程序先后出现,如SAP,ALGOR.ANSYS,ADINA,MARC,ABAQUS等。程序吸纳了固体力学领域最新的算法技术,将求解的固体力学问题通过离散的有限单元来近似模拟,使得由于复杂的边界和构造带来无法用函数求解的固体力学问题可以采用数值方法的手段获得较为准确的模拟结果,这些程序为土木、机械、航空领域带来了革命性的变化与推动。经过近40年的发展与完善,分析程序均已经具备完善的构架与功能,求解的问题也随着理论算法的改进获得更新与完善,求解的问题也已经由早期的单场问题扩展到多场问题。
国内较早引入CAE分析程序源于20世纪80年代初,主要集中在机械设计领域。20世纪90年代,这些程序逐步引入到土木工程行业,解决了很多传统手段无法解决的结构分析问题,也创造了形式丰富的设计作品。这期间,国内的研究人员也加快了开发步骤,一批能够解决特定问题的有限元程序也先后涌现。
程序大致分为3类,一类主要面向工程设计,如STADPRO,ETABS,GTSTRUDL,STRAP和3D3S等,程序具备基本的静力和动力分析模块,同时内嵌该区域的设计规范,依据分析结果,可进行设计校核,对以杆系单元为主的结构工程,基本能够胜任,但其单元库较少,可设置边界条件较少,总体计算能力一般。第二类程序也主要面向工程设计,兼具了部分通用程序的特征,如Sap2000,MIDAS系列等,这类程序单元库相对较多,能够设置一些复杂的结构边界,同时具备线性和非线性求解能力,能对几何非线性问题、材料非线性问题以及过程非线性问题进行基本求解,因此,适应面较广。但这一类程序主要面向杆系单元为主的结构工程,面向壳体和实体分析时,由于不具网格划分能力,因此,限制了其使用范围。第三类程序便是以ADINA,ABAQUS,MARC,ANSYS等程序为代表的大型通用CAE程序,这类程序具备了较为完善的前处理、计算、后处理能力,单元库丰富,边界设置适应范围广,算法先进,几乎可以求解土木工程领域现阶段的任意工程问题,因此,也获得了工程师们的青睐。但这类程序对工程师的力学分析能力和结构概念要求较高,因此,其使用人群主要还是局限在高校为主。
现代大型有限元分析程序,大都具备如下几个基本的技术特征:
1)CAE的一个发展方向便是和CAD无缝集成,现代CAE程序大都已经具备一定的几何建模能力,几何模型格式一般采用国际主流的PARASOUD格式,便于后期几何模型的编辑运算。但其建模能力往往难以应付复杂的工程问题,因此,这些程序一般都具备较好的几何模型导人接口,常用的X_T,SAT,IGES,STP格式几何一般均能导入CAE,这样便可以采用专业的三维CAD程序完成计算用几何模型的建立。但由于CAD软件几何建模的尺寸误差,这些模型在导入CAE程序以后,均需要进行修复处理,如骨架线框形成交叉点、实体的连续过渡、曲面的修补、重复几何点的合并等。可以这样说,几何模型的编辑修改能力,是CAE前处理能力的一个重要标志。
2)形成结构离散的直接方法便是几何网格的划分,对于杆系为主的单元划分,所有的CAE程序都不在话下,CAE程序网格划分能力主要体现在对自由曲面的四边形网格划分以及由自由曲面包围形成的实体六面体单元网格划分上,大多数CAE程序均采用结构化网格和自由网格两种划分思路,对于复杂的工程节点分析,如铸钢节点、球杆相贯节点,往往难以采用结构化网格,因此,需要程序具有较强的自由网格划分能力。网格质量好坏的基本判断,便是网格与几何模型的贴体性,实际工程的几何边界非常复杂,往往难以与结构整体坐标相符,因此,需要用数学构造方法构成贴体坐标系。目前,CAE程序的贴体坐标系生成方法,主要是代数法和微分方程法。
3)有限元仿真的难处在于对边界的模拟,主要包括结构边界、单元边界,传统设计认为,地面就是刚形体的假定在某些大型复杂工程中并不准确,因此要求采用各种连接单元模拟单元与边界的耦合作用,边界单元库以及其设置是CAE程序求解能力的一个重要反映。
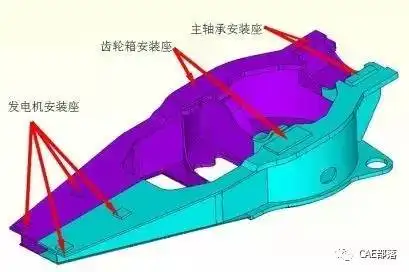
4)快速高效的非线性与线性算法对现代大型工程越来越重要,虽然依托电子计算机的高速发展,上千万个自由度的大规模问题求解已经能够在PC机上实现,但工程设计的不同,便是在于设计方案调整的反复性,因此,往往需要CAE程序高效快速的计算能力满足反复试算、方案调整等,现代大型CAE程序往往都已经具备快速高效的计算方法,常用的如NR法、M-NR法、AL法、BFGS法等,都能够满足高效快速准确的计算要求。
5)现代工程设计已经从固体力学领域逐渐渗入到温度场、流场等领域,如厚钢板焊接的温度残余应力模拟、风一结构耦合作用、屋顶水箱制振耦合作用等,主流的大型CAE程序一般都已经具备这些问题的耦合计算能力,在单一的计算平台下,能够实现多场单次耦合或者多次耦合计算。
这些技术特征直接反映了CAE程序的求解能力,要充分驾驭这些技术特征,对工程师无疑是一个艰巨的挑战,需要使用者具备宽泛的知识结构与深入的专业概念。下面,就CAE程序与土木工程结合使用的几个重要环节,对一些关键概念进行论述。
2 几个数学概念
工程结构分析中广泛应用到一系列数学工具,典型的如离散与集合、变分原理、随机过程、富利叶变换、张量分析等,对这些数学概念的理解与应用,将直接关系到结构分析的质量。因此,就这几个概念问题并结合笔者的认识与体会进行论述。
2.1 离散与集合
离散与集合是有限元方法的精髓。有限元法把求解区域看成由许多小的相互连接子区域或单元构成,即它是利用一组离散单元的集合体来代替求解区域,其性态由若干个参数来表达。
这些参数所表达的离散体的数学方程称为形函数,再将全部离散体的形函数集成,组集成一组高阶的线性或者非线性方程组,从而求解作为单元集合体的整个系统。由于单元的剖分是任意的,并且可以按照不同方式组合在一起,所以能够灵活地表达非常复杂的几何形状。随着数值计算技术的发展,即使离散体或者自由度的数目非常大,也较容易实现。这种由离散体近似表述整体问题的方法,可以是传统的数学近似或者是工程上的直接近似。
于是在有限元法中,离散的概念包含两个方面的内容:其一是结构的单元划分,用有限个单元体来近似代替整个结构,每个单元的力学特性可以通过实验或者数学上的推导来完全确定;其二是单元的集合,即对每个单元所确定的特性关系进行求和,这是一个很有规律且非常简便的过程,因为每个单元的刚度系数可以直接存放到整体刚度矩阵中对应的位置上。需要注意的是,由于不同的单元具有不同的特性,因此,在集合单元刚度矩阵时,应该满足矩阵求和的规则,只有阶数相同的矩阵,才能够相加,因此,要相加的各个子矩阵,必须由力或者位移分量数目相应的项组成。离散与集合的思想,使得许多复杂的结构问题的求解成为可能。
2.2 有限元与随机分析
随机分析与有限元方法的结合便是所谓的随机有限元,或者称为概率有限元法,这种分析方法结合了有限元的离散集合与概率随机过程的数学思想。
在工程领域,存在许多不确定因素,如结构的物理参数、几何参数及其承担的外荷载(例如风荷载、地震作用等)。由于人们认识的局限性和这些参数(现象)本身的不确定性,这些因素被描述为空间或者时间的随机函数或者随机过程,同时,这些随机因素的影响是不可忽略的,致使结构行为不再是确定的,而具有偶然性,表现为随机的场函数和时间函数,经过确定性的结构分析之后,人们还需要了解结构行为函数的概率分布,而随机有限元分析,正好能够解决这样一个问题,随机分析求得的结果因此不再是具体的结构响应量(如力、位移),而是力或者位移的概率统计量。
一般地,随机分析可以分为两类:一类是统计方法,就是通过样本试验收集原始的数据资料,运用概率和统计理论进行分析与整理,然后做出判断。这种方法需要进行大量的样本试验和数据处理,且计算工作量巨大,目前高速计算机使得模拟法成为最通用的统计逼近法,如蒙特卡洛法。
另外一种方法是非统计法,这种方法在本质上是利用分析工具找出结构系统(确定性系统和随机系统)输出信号和输入随机信号之间的关系,这种方法无需进行大量的样本试验,而是采用随机分析与求解系统控制方程相结合的方法得到输出信号的各阶随机统计量的特征,如各阶原点矩(或者中心矩),这个方法最大的优点是不需要完全了解输入随机信号的数值特征,仅仅需要知道一定阶次的信号数值特征,运用解析或者数值的方法,便可以得到一定精确度的解。
目前所谓的随机有限元方法,包括摄动随机有限元法、纽曼随机有限元法和蒙特卡洛随机有限元法,其中摄动有限元法采用最多。CAE程序大都采用的是蒙特卡洛随机有限元法。
2.3 富利叶变换与拉普拉斯变换
积分变换是求解数理方程的有力工具。其中,富利叶变换和拉普拉斯变换常用来求解常系数偏微分方程,通过变换,将原函数的微积分运算化为变换函数的四则运算,以便于方程的求解。富利叶变换常用到动力学或者结构振动的问题中,原函数是时间T的函数,变换函数是谱量ω(工程上便是频率域)的函数,因此,富利叶法在工程上也称为谱分解方法。
它不仅能够使方程的求解更加方便,而且可以确定振动问题的谱密度,这是振动问题中一个重要的测度,利用谱密度可以直观地看出振动能量在频率域上的分布,从而找出工程结构有效的抗振措施。拉普拉斯变换是考虑振动体在T=0时开始受到外界影响,如施加荷载以后结构的各种物理变化,特别适用于如土壤的固结理论和混凝土的徐变理论。
富利叶变换有两种形式:一种是三角函数形式,另外一种是指数函数形式。一些数学文献将拉普拉斯变换从富利叶变换的理论推导出来,不过从解决实际问题来看,拉普拉斯变换绝非富利叶变换的一个变种,富利叶变换的原函数自变量从-∞到+∞,而拉普拉斯变换自变量仅从O~+∞,这一点非常重要。物理世界中的各种动力激励绝对不会在宇宙中至始至终、恒存在,而是从某一个相对时间T=0开始作用,求解这个激励引起的动力响应,拉普拉斯变换恰好符合这样一个要求。在预应力混凝土设计和建筑物基础设计中,人们希望知道预应力的长期损失和建筑物的最终沉降,这些问题便是一个典型的拉普拉斯变换问题。
2.4 变分原理
在物理与力学中有很多问题需要采用变分原理,如弹性静力学中的最小势能原理,动力学中的哈密顿原理,塑性力学中的变分原理。变分原理在计算力学中特别重要,一方面,按照变分原理可以用李兹法或者伽辽金法获得结构近似解;另一方面,变分原理也是有限元法的基础。变分原理的几个经典理论是虚功原理、最小势能原理和最小余能原理,具体原理的推导,可以参考一般的有限元理论专著。
在弹性力学中一般可以找出一个变分泛函,使泛函取极值,得出全部控制方程和边界条件,这是变分原理的优点。用变分原理求取近似解和虚功原理是等效的,但是具有更统一的形式。不过需要注意,在一些情况下,不能找到一个变分泛函,但是仍然可以采用类似虚功原理设法求解。最小势能原理和最小余能原理以及余虚功原理,实质上是相通的,不再赘述。
3 CAE程序结构设计的几个概念
CAE程序实际上是数学原理和力学理论结合的产物,其大多数关键设置、参数输入、求解方法,均可以在数学和力学理论上找到其影射点。因此,一套计算方法可以应用于不同的行业,结合专业,灵活使用这些基本的概念,对提高分析适量、结果判定,具有举足轻重的意义。下面,就CAE在结构分析中的几个概念进行论述。
3.1 单位系统选择
建立物理模型的一个基础,便是模型单位系统的选择,大多数CAE程序都没有规定专门的单位系统,仅要求参数所设定时对应的力学单位和几何单位必须封闭,即单位必须统一。
1)对静力问题,只涉及到3个单位系统:长度、力、弹性模量,因此,只要作到这3个单位统一就行了,如长度的单位用m,力的单位用N,则弹性模量的单位为N/m2,而应力的结果自然也就是N/m2。
2)考虑重力时,必须输入密度和重力加速度的值,对于静力问题,输入密度和重力加速度的作用就是为了让程序根据其输入值计算重力,因此,对同一问题,在其他输人参数完全相同的情况下,只要保证密度和重力加速度乘积相等,则计算结果完全相同,此时需要协调的就只有长度、力和弹模,但对于动力问题,由于单位不协调,这个结论不成立。
3.2 几何连接关系
建立几何模型需要定义单元之间的连接关系,这不仅影响到结构分析结果的正确性,有时候还会直接导致后续分析无法进行。结构有限元分析中,常遇到的两个问题如下。
1)单元之间形成了多余的连接节点,主要体现在两个方面:
其一为单元在连接处生成重复节点,单元表面上交接在一起,实际上节点并不连续,导致单元内力无法传递,严重的时候,还会导致单元产生刚体运动,后续计算出现刚度矩阵奇异的错误提示,解决办法为消除多余节点即可;
第二种情况常出现在非线性单元交叉处,以钢结构工程中常用的柔xing交叉支撑为例,通常用索单元模拟。如果计算模型中将索单元在交叉处打断形成共享节点,则将导致单元在交叉点处约束不足,形成刚体运动,计算出现刚度矩阵奇异错误。其解决办法为将交叉节点消除,单元直接连通即可。
2)单元之间没有形成连通域,这种情况主要反映在精细化局部实体分析的时候。根据CAD建立的几何模型通常为多个零件(PART)组装而成的组件(ASSEMBLE),零件之间的交界面仅在几何上接触,并无共享的接触面、线、点,即零件之间没有形成连通域,其直接后果便是单元划分以后,网格完全不连续或者局部不连续,单元零件之间无法传递力学响应结果或相互的约束,甚至造成刚体运动,求解失败。其解决办法是在CAD程序里面进行布尔运算,通过切割、交集、并集等手段实现几何体的连通。
3.3 单元选择
CAE分析中广泛使用到一系列单元,如梁单元、桁架单元、索单元、实体单元、壳体单元、平板单元等。选择不同单元的原则有两点:其一为分析所需要考查的信息,比如混凝土梁,当仅关心的单元宏观的内力响应指标,如弯矩、剪力、轴力时,则采用杆系梁单元,即可以采集到工程所需的力学指标。
但是,当需要考察混凝土梁的裂缝开裂、应力沿断面的分布状况时,则需要采用实体单元,再比如混凝土板,当需要考查其带裂缝工作性能时,则需要采用实体单元,否则无法获得裂缝在板厚度方向上的分布情况。
当然,个别CAE程序采用在壳单元厚度方向上增加积分点的方式来近似模拟板厚度方向的力学响应结果,则另当别论。其二为根据具体工程单元主要工作特性,在工程分析中,有些时候工程师容易犯形而上学的错误,以索单元和梁单元为例,当结构分析需要考察的是构件的受拉特性,或者说构件实际工作特性主要以受拉为主的时候,这时候可以采用索单元模拟,但是,当需要考察柔性构件的垂度效应时,则可以采用降低抗弯刚度和抗剪刚度的梁单元来分段模拟拉索,从具体构件的工作特性抽象出对应的力学模型,是单元选择最重要的原则。
再比如桁架单元和双向铰接梁单元的选择,当铰接构件主要呈现拉压特性时,可以采用桁架单元模拟,但是,当铰接构件还需考察横向变形特性时,则应该采用铰接梁单元模拟,开口薄壁型钢构件,由于其截面翘曲作用有时候会增加很大的额外附加应力,此时,则需要考虑采用带有翘曲自由度的梁单元模拟,否则,分析结果在工程上存在不安全因素。

3.4 单元划分与荷载传导
和一些专业的设计程序不同,CAE程序形成结构物理模型最关键的一步,便是单元网格划分,有限元的所有力学响应指标,均是通过单元节点进行传递,并保持位移连续。
工程中常见的一个错误,便是梁系框架没有单元划分而造成错误结果,其问题主要在于单元划分和荷载传递的问题:大多数情况下,为了提高计算效率,CAE程序默认的单元均采用线性积分单元,这样,在一个单元体内,其输入激励和响应指标呈线性分布,因此,当输入荷载后,最终通过节点传导,单元体中间区域并没有传导荷载,造成节点受力,单元并没有受力的现象。
一个简单的例子便是计算楼盖结构,假定梁单元划分数量为1,其包围的板壳数量也为1,则最终计算的时候荷载均传递到了梁柱节点处,板和梁均处于空载状态,这样的分析结果无疑是错误的。解决办法很简单,细化梁单元和板单元网格,并保持网格连续。
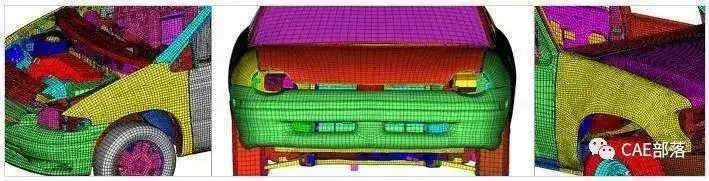
3.5 节点自由度连续
CAE程序中各种单元都有其对应的自由度,比如梁单元每个节点为6个或者7个自由度(除了常用的平动和转动自由度以外,薄壁构件还有翘曲自由度),桁架单元每个节点有3个自由度,壳体单元每个节点有6个自由度,实体单元每个节点有3个自由度。
当结构分析混合使用这些单元的时候,需要注意其自由度的连续问题,比如采用实体单元模拟基础,壳体单元模拟剪力墙,由于单元节点自由度的不连续,会造成剪力墙根部无法和基础实现转动协调,如果剪力墙处于悬臂工作状态,还会引起墙体单元转动约束不足,形成刚体运动。解决办法是根据力偶的概念,将墙体根部交接区域两侧实体单元的节点和墙板根部节点进行自由度耦合。类似的例子,如梁单元和实体单元的连接,也存在相同的问题和处理手段。
3.6 边界模拟
现阶段CAE程序对杆系模型的分析已经达到了一个相当的精度,杆系单元的模拟和实际工程单元工作性能的比较精度很高。但是,现代CAE模拟的一个难题,便是边界处理。传统的工程分析,假定地面为无限刚,则可以将结构边界约束点按工程构造简化为铰接或者刚接,这对大多数工程是有效的。但是,现代结构的体量越来越大,上部结构传递到柱脚的内力很多时候达到了惊人的程度,因此,传统的假定在这些情况下应该慎重对待。同时,由于构造处理和分析假定的误差,在边界区域,节点的受力往往远远比按照杆系结构分析得到的结果危险。
没有精细分析的设计,往往在这些区域形成设计真空,留下安全隐患。在此,主要谈一下上部结构—基础耦合计算的问题。这个课题包含的内容很多,包括基础—地基耦合,基础—结构耦合,结构—基础—地基耦合等。其仿真分析的难处,主要在于各个部分接触面的有限元模拟,根据笔者的工程实践,以钢结构一基础耦合计算为例,提出3种适合工程的模拟方法。
1)在柱脚和基础顶接触面上设置桁架单元,桁架材料属性设置为只受压特性,即在受拉的象限内,应力为零的时候,应变很大。这种方法的特点是:适应性较广,多数具备非线性求解能力的程序均能胜任,且计算结果较准确。但该方法无法考虑初始间隙,其实质是无初始缝隙的间隙单元。
2)直接采用间隙单元,功能强大的CAE程序均有此功能。该方法的特点是:方便、结果较准确、可以考虑初始间隙,但求解参数设置多一些。
3)直接采用接触分析,具体过程很简单,在上下两个面之间设置接触对就行了。该方法的特点是:结果最准确、假定少、但设置较麻烦,一般设计工程师操作困难。
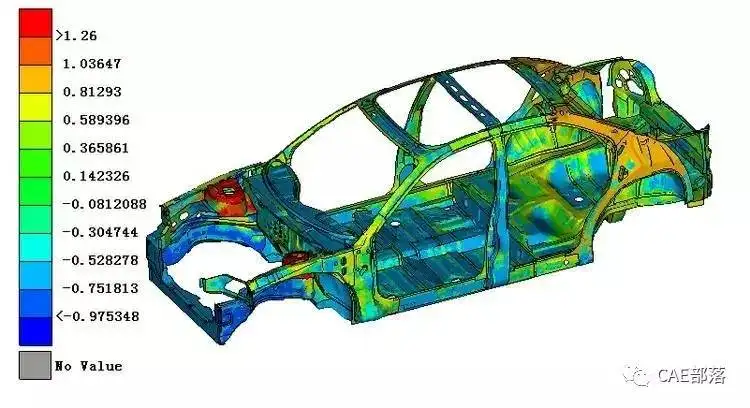
3.7 动力分析
对于复杂的结构工程,动力分析是必不可少的一个环节。动力分析的方法,一般可以采用频域的反映谱迭加法和时域的瞬态动力积分法。除了直接积分法以外,动力分析常要求以模态分析为基础。下面,就动力分析中的几个常见问题进行探讨。
3.7.1 模态质量的选择与判断
大多数专业的设计程序均能按规范的规定将全部恒荷载和部分活荷载按照等效质量集中在结构质量对角矩阵中,但是,CAE程序往往需要人为干预,CAE程序一般提供了质量单元。因此,为了充分考虑质量在振动过程中的动力效应,需要按照荷载的分布特性,将以荷载形式出现的等效质量转换为质量单元参与结构动力计算。否则,CAE程序将仅仅按照模型单元的自重进行动力计算,显然,这样的计算结果对动力响应估计过小,会造成安全隐患。
大多数设计规范均要求结构振动有效参与质量不低于等效总质量的90%,这是为了保证充分估计结构的动力效应,CAE程序一般都提供了这样一个功能,可以在模态分析结束以后提取质量参与系数来判断模态数量是否满足要求。
3.7.2 周期折减系数的模拟
周期折减系数是工程设计上的一种近似处理手段,其原因有二:其一为考虑结构围护构件对整体结构刚度的增大作用;其二为地震反应谱的峰值段主要集中在高频阶段,折减自振周期可以使结构在振动中获得更多高频振动激励,从而达到偏安全的作用。绝大多数CAE程序都不提供自振周期折减设置,解决该问题的办法有二:其一为CAE程序提供了广泛的模拟能力,围护构件可以整体建模参与整体振动分析,因此,无需再对其刚度增大作用进行假定;其二为将主结构弹性模量同时放大1.2倍左右,考虑围护构件刚度增大作用,但是,这种方法对内力分析结果有诸多不利影响,需斟酌使用。
3.7.3 重力加速度的处理
瞬态动力分析的初始条件有两种:其一为直接在零时刻开始进行瞬态动力计分计算,然后将瞬态动力分析的结果和其他荷载的分析结果进行迭加组合,这种方法对线性结构有效;其二为以前期荷载分析的结果作为初始状态,进行后续瞬态动力分析,这种方法适用于非线性和线性结构,具有广泛的适应性。这一过程需要注意的是,由于瞬态分析在数学上为一个三维数值积分过程,其初始条件对后续积分结果有直接影响,瞬态分析的初始时刻,结构加速度为零,如果以重力加速度作为初始条件,等同于积分初始过程引入了很大的初始值,这样得到的结果往往不是一个平稳结果,而是衰减曲线。因此,重力加速度只能作为一个贯穿瞬态过程的稳态量来处理。简言之,重力加速度在瞬态分析中,没有加速度意义。其解决办法,只需要在时程激励初始时刻强制将加速度设置为零即可。
3.7.4 行波效应的处理
在大跨度工业与民用建筑中,需要考虑地震波的时滞问题,即通常所说的行波效应。在现有CAE程序中,除了ABAQuS和LSDYNA以外,绝大多数CAE程序均不具备直接的行波效应设置能力,但是可以通过变通的手段来解决,其方法如下:
1)在结构基地设置大质量单元,单元质量一般在结构总质量le6数量级以上,然后,将加速度激励放大le6倍,直接以力时程施加在结构基底;
2)将加速度时程转换为位移时程施加在结构基底。
两种方法需要注意的是:其一,结构基底在激励方向不能约束;其二,分析得到的分析结果是数学意义上的绝对结果,要采集结构响应结果,还得将结构响应直接积分结果减去基底响应结果。
3.8 结果应用
分析结果正确性判定需要工程师具备丰富的结构概念,数值模拟计算,由于其建模分析始终带有各种各样的计算假定,因此,无论单元划分如何精细,边界处理多么完善,荷载激励取值多么准确,其计算结果始终是近似结果。总体而言,有限单元位移的连续性假定,保证了其位移分析结果相对精度更高,而内力和应力计算结果,则容易受边界假定、单元积分模式、网格划分等的影响。从工程的角度出发,笔者对数值分析结果选用进行说明。
1)杆系单元由于其假定相对较少,单元对网格划分精细程度不敏感。因此,其内力分析一般均可以直接采用,准确程度较高。
2)板壳单元和实体单元受单元积分模式影响,结果震荡相对较大。一般来说,四边形单元比三角形单元结果准确,六面体单元比四面体单元结果准确。
3)数值分析结果为单元积分点上的数值,即单元响应结果,以积分点结果为基础,向外插值以后得到节点上的结果,因此,数值精度上积分点结果比节点结果更高。同时,由于CAE程序一般对节点积分进行了均化处理,因此,节点平均值往往比单元积分结果小,从工程的角度来说,采用单元分析结果偏安全。
4)对于混凝土等脆性材料结构的分析结果,一般采用第一强度理论进行结果判断,而对于钢结构等塑性材料结构,则采用Von.mises屈服准则进行结果判定。
5)混凝土类结构分析的内力结果,可以直接作为后续配筋计算的依据,而钢结构分析得到的应力,则不能直接作为构件安全性能的判断依据,还应根据其内力计算结果结合规范进行构件强度校核。
6)由于使用有限单元划分,力学计算单元和工程单元在尺度上存在差异,因此,工程意义上的构件计算长度在CAE分析中得不到体现,特别是在钢结构工程中,工程师对构件的稳定计算更不能直接依托CAE杆件应力分析的结果,根据CAE内力分析结果进行稳定校核,是必须的工作。
4 结语
CAE分析引入工程建设,无疑将在很大程度上提高工程结构的设计水平,但对于力学分析和依据行业规范的参数调整,则是保证分析结果准确性的基本前提,灵活的应用力学概念和结构概念,则是工程师提高分析水平的关键。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删