技术范例：周期性振幅的模拟与分析

前言：

在仿真当中，外力及边界条件经常透过振幅Amplitude来控制，在Static, General分析步经常用Ramp振幅(斜直线)来控制；在Dynamic, Explicit使用拟静态手法时，会搭配Smooth step平滑加载曲线。本文介绍另外一种常见的週期性振幅Periodic Amplitude如何使用。

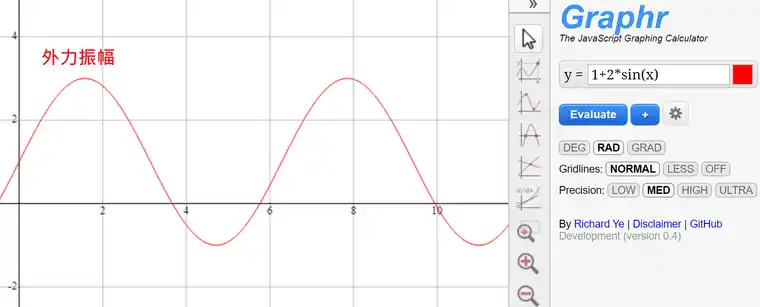
週期性函数：

週期性函数都可以用傅立叶函数(Fourier series)形式展开，在此不特别介绍，直接看帮助文档对其定义以及在Abaqus需要给定的参数。如下图所示，透过圆频率、时间偏差、上下偏差以及An, Bn来定义週期性函数。

范例：

An, Bn分别对应馀弦与正弦函数的振幅，以首张图片的週期性函数为例子，是以单纯正弦函数形式，傅立叶展开只需要取一项n=1，因此给定B1项次，A1=0，圆频率先量测週期T(波峰与波峰间距)，透过公式w=2pi/T得到圆频率w=1，时间偏差用来描述这个图形的左右偏移，先假设是0，后面会针对这个部分做调整，上下偏移即是图形的上下移动距离，可以理解成原点到平均值的距离(原函数向上或向下移动的距离)，以本范例来说，移动的距离是1，最后给定的参数如下图。

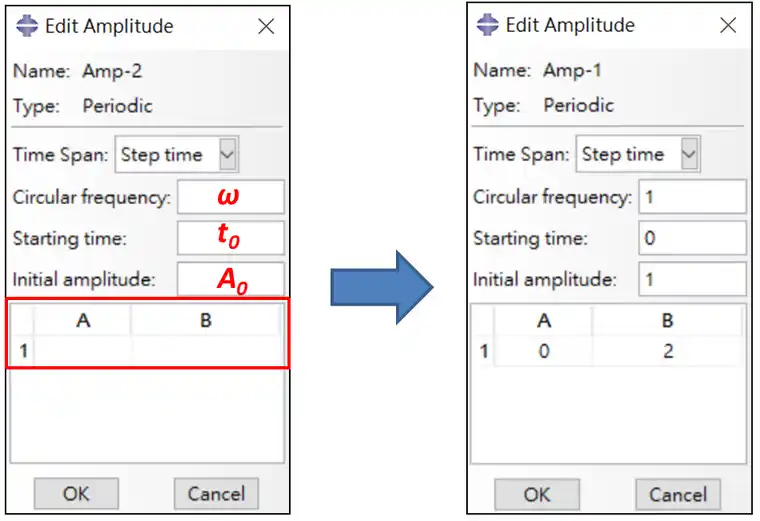
实测：

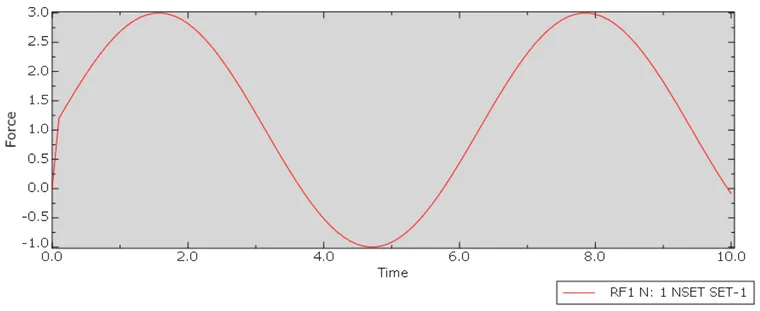
採用truss元素进行实测，给定一端週期性外力，量测另外一端反力作验证，在Static, General分析步下回得到的是静力平衡的结果，模型设定在此不多赘述，结果如下图。

对时间偏差修正：

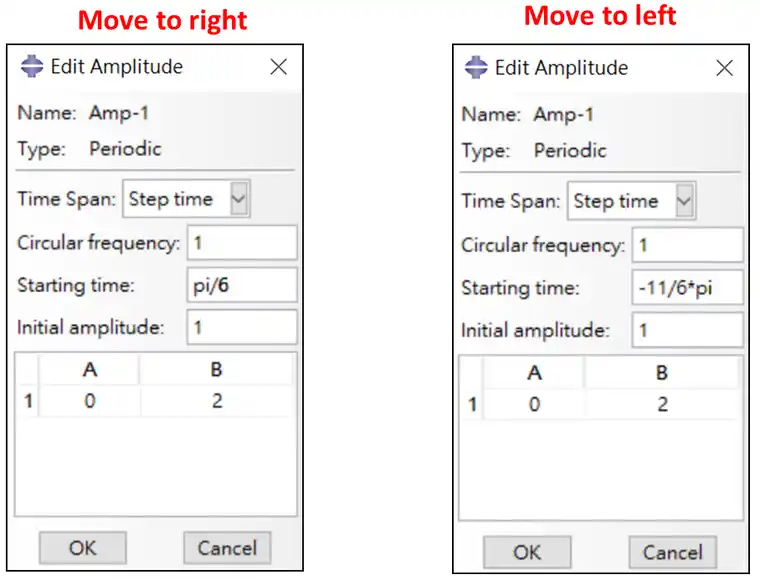
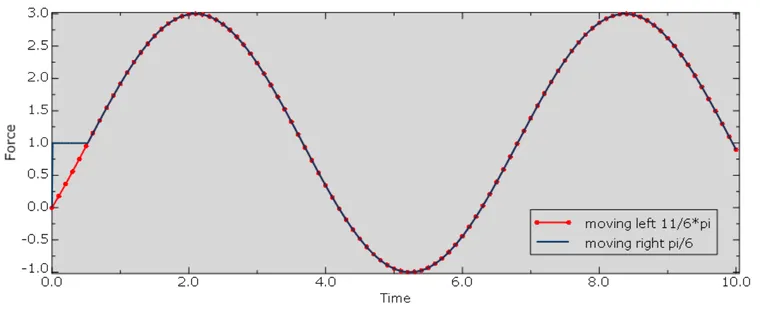
在初始的时间，因为从原点开始，会有一小段偏折，大多数情况会以平滑的方式加载，因此可以透过时间偏差来修正，但是特别注意，根据帮助文档的定义，若t<t0，则函数会等于A0。继续以上面的范例，假设希望初始时间的函数值等于零，可以对图形左右偏移来调整，下图显示向左向右移动的结果，向右移动pi/6跟向左移动11/6*pi的图形完全一样。

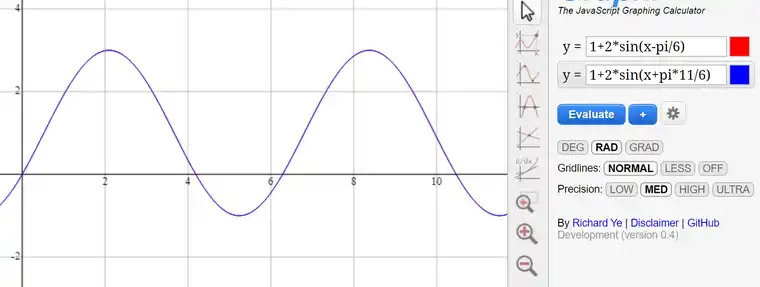
结果比较：

振幅设定与结果比较如下图，儘管在週期性函数上两者的定义都是相同曲线，但在设定上必须注意其定义，t<t0的时候，a0=A0。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删