不同切削深度下的二维岩石切削模拟分析

线性切削广泛应用于岩石的数值试验中，在线性切削过程中切削刀具以设定的速度划过岩石表面，同时以不同深度切削岩石，切削破坏表层部分岩石材料。使用ABAQUS有限元软件建立单刀线性切削岩石材料仿真模型，研究切削深度对岩石切削中切削力的影响。

1.计算模型

运用有限元显示动力学分析方法进行仿真模拟计算。在有限元模型中，岩石材料模型的长度为20mm，高度为5mm的长方形，刀具为长3mm，宽1mm，倾角为15°。

如图所示为岩石单刀线性切削模型示意图。将切削刀具视为刚体，岩石材料剖分为6000个单元，岩石采用平面应变四节点双线性减缩积分单元(CPE4R)，且将被切削部分的岩石进行网格细化，保证精度的同时提高计算效率。

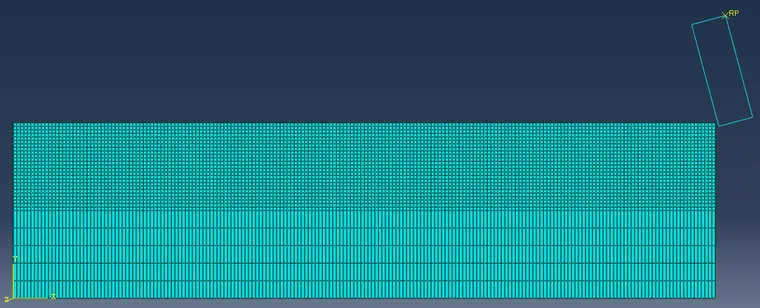
单刀线性切削岩石材料的仿真计算十分复杂，为了提高计算效率和便于分析，忽略次要影响因素，对该模型做出如下假设：

1)当岩石材料单元失效后即从模型中删除，忽略其失效后对后续切削的影响。

2)切削刀具的强度和刚度远高于岩石材料，将刀具假设为刚体，且在切削过程中不发生磨损。

3)不考虑温度对切削过程的影响。

2.计算参数

密度：2600kg/m3

弹性模量2000000000pa

泊松比0.3

断裂应变0.002

内摩擦角41.84°;

剪涨角5°;

屈服应力10900000pa

失效位移0.0001

3.计算工况

切削速度为15mm/s，切割时间为0.5s，质量缩放为10000。

建立切削深度为0.1 mm -1.8mm共18个工况。

将切削刀具视为刚体，在切削刀具上设置参考点RP来约束其运动，这样不仅便于切削力的提取，也便于对刀具施加约束条件。本模型中岩石材料与刀具之间的接触采用Node-to-Surface接触，即在每一个增量步都重新定义接触，从而实现切削过程中岩石与刀具的动态接触，法向接触为硬接触，切向接触面采用罚函数来定义摩擦，取摩擦系数为0.3。

4.云图分析

选取切削深度分别为0.1mm、0.5mm、1mm、1.4mm、1.8mm的mises应力图如下。

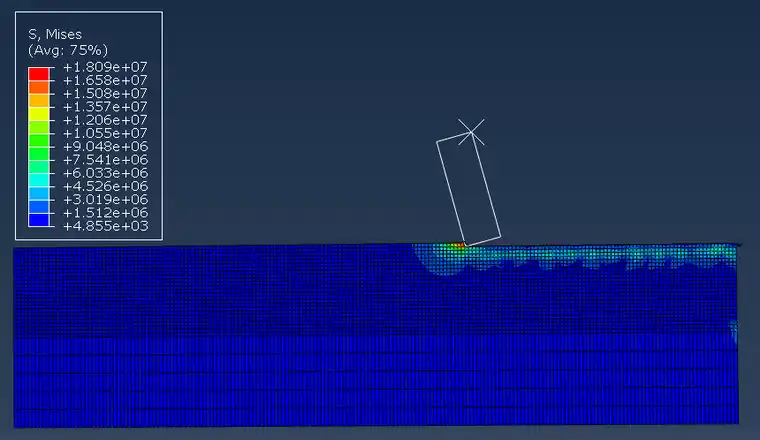
图1切削深度0.1mm

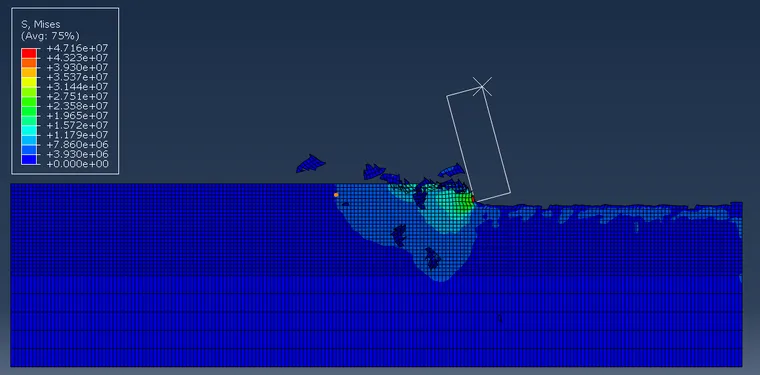
图2切削深度0.5mm

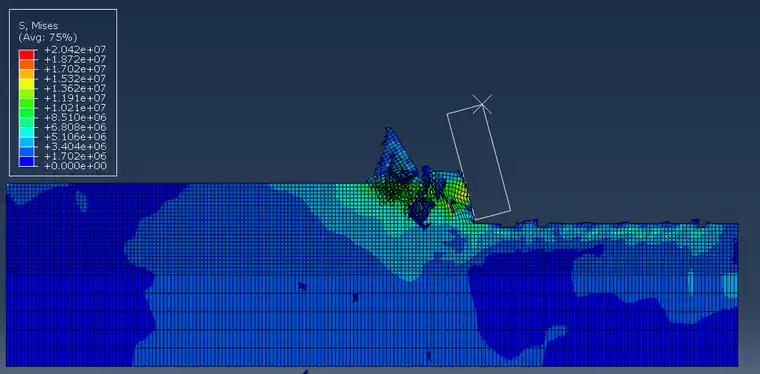
图3切削深度1mm

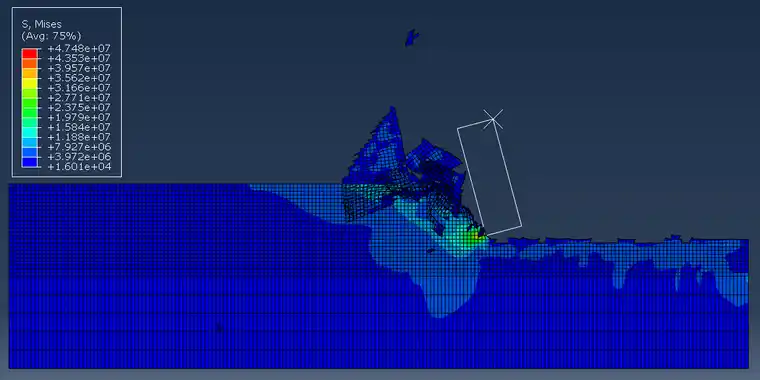
图4切削深度1.4mm

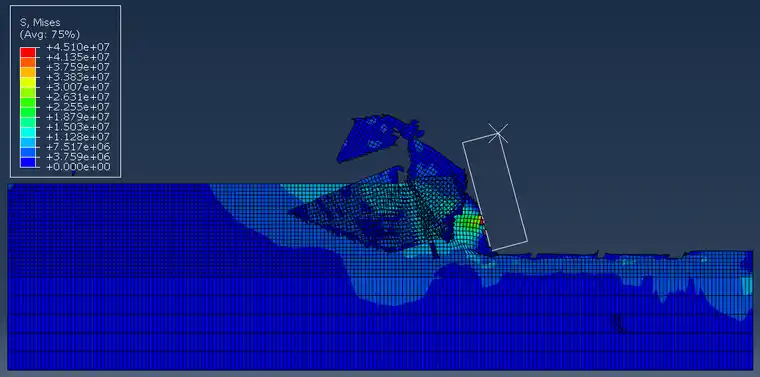
图5切削深度1.8mm

选取切削深度分别为0.1mm、0.5mm、1mm、1.4mm、1.8mm的mises应力图。我们可看出随切削深度的增大，应力分布区域增大，切削碎屑形状增大。

5.切削力分析

岩石在刀具切削作用下的破坏形式不仅可以从碎屑形状和应力分布云图来判别，也可用切削力来描述，实际切削过程中切向切削分量和法向分量并不是一个恒定值，并且在切削初段和末段有较大的波动，所以它们的合力也不是一个恒定值，因此本文通过截取一段较为平稳的刀具力学反馈数据来计算切削力合力的平均值。如图所示为岩石材料在不同切削深度下切削力与切削深度的关系曲线。

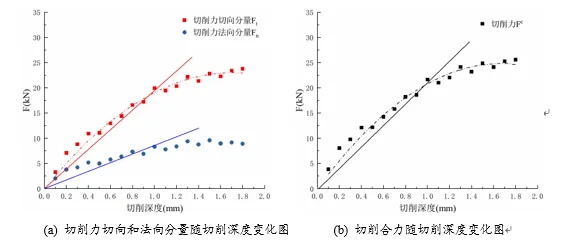
由图可知，切削力与切削深度的变化规律基本上可以分为两个阶段，即线性段和非线性段。当切削深度小于0.9mm时，切削力以及切削力的切向分量 、法向分量均和切削深度呈线性关系；当切削深度大于0.9mm时呈现出非线性关系。

6.结论：

1）当切削深度较小时，岩石的破坏主要是以表层的岩石材料为主，特征主要是被破碎的岩石碎屑在切削刀具前端不断的堆积和塑性流动，且切削碎屑比较碎小，切削面相对平坦。当切削深度较大时，主要是应力区域在切削刀具的前端不断积累，应力向自由表面扩散较为明显，且切削碎屑比较大，切削面更为粗糙。

2）由切削过程中的应力云图及切削碎屑的大小可知，随着切削深度的增加，应力区域逐渐向切削刀具前端累积，切削形成的碎屑也不断增大，切削面的粗糙度逐渐由平坦转变为粗糙。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删