工具路径-网格交叉模块
工具路径-网格交叉模块计算增材制造过程中使用的各种工具路径和被制造零件的有限元网格之间的几何交叉点。
1工具路径-网格交叉工具路径表示
刀具轨迹表示机床的一个给定部件的运动,例如激光源、重涂辊或送丝喷嘴。工具路径是由附着在沿着路径移动的参考点上的几何形状定义的。路径是通过连接空间和时间上的点集合来定义的。事件系列定义了点的集合。事件系列中定义的第一个字段描述了该工具的状态,例如激光功率、重涂辊的“开/关”状态或送丝喷嘴。这个字段在两个连续点之间假定为常数。值为零的字段表示工具的“关闭”状态。
工具路径-网格的交点考虑了三种形状:一个点,一条无限的线,和一个盒子(见图1)。这些形状提供了不同的抽象层次来描述工具的形状,这取决于特定的应用。除了这三种形状之外,还可以使用扫描样式来描述工具的理想运动,而不是运动的实际路径。下面的主题列出了由工具路径-网格交叉模块为每个形状和扫描样式计算的一些数量。有关模块计算的数量的完整列表,请参阅数据检索功能程序中的表。
| 形状 | 点 | 无限长的线 | 盒子 |
| 样式 | |||
| 机器工具例子 | 粗糙网格的点激光 | 粉末床制造中的重涂辊 | 细化网格中的聚合物拉伸,线材供给,激光的材料沉积喷嘴 |
2点形状工具路径-网格交叉
当工具的行动区域相比较于网格尺寸,非常小时,工具形状的点表示是有用的,此时可以将工具形状理想化为一个点;例如,当激光束的半径与单元的尺寸相比,非常小的时候。
图1描述一个点工具路径与一个有限元网格E的交叉点。工具路径通过时间(t1,t2,t3,t4…..)时的路径连接点(X1,X2,X3…….)定义。假设工具在连接路径上两个连续点的线段上以恒定的速度运动。事件系列中定义的第一个字段表示工具的状态,比如激光功率。为点Xn定义的字段,在连接Xn和Xn 1的分段上,保持固定。工具处于“on”状态的路径分段必须与全局Zg方向垂直。对于一个给定的单元,工具-网格交叉点模块计算工具路径交叉点的数量,开始点和结束点的坐标(分别是ζs,和ζe,在单元参考坐标系中表示),每个交叉的起始和结束时间(ts,te)。
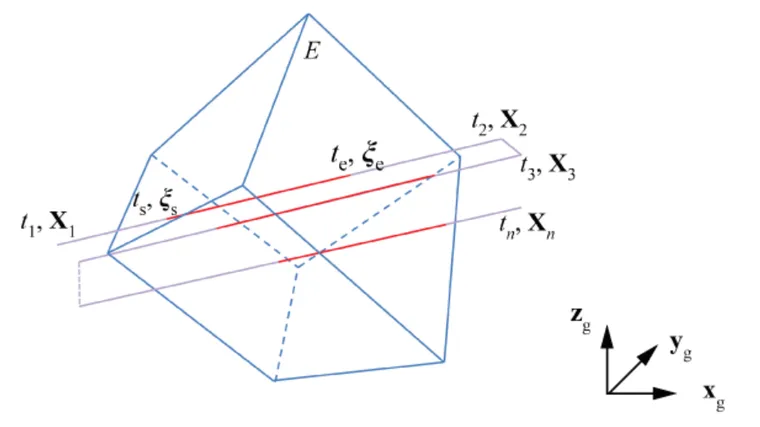
3无限长的线表示的工具路径-网格交叉
刀具形状的无限长的线形状表示,对于描述材料逐层沉积的过程是有用的,例如重涂辊在粉末床加工中的操作。
图1描述了无限长的线形状工具路径与有限单元E的交叉点。工具轨迹被定义为连接到一个沿着轨迹连结点(X1,X2, X3,…,Xn)移动的参考点的无限长的线,例如在时间ti,Xi位置的参考点。假设工具在路径上连接两个连续点的线段上以恒定的速度运动,而无限长的直线垂直于线段。事件序列中定义的第一个字段表示工具的状态,例如重涂辊的“开/关”状态。为点Xn定义的字段在连接Xn和Xn 1的线段上保持固定。当工具处于“开”状态时,所有路径线段必须垂直于全局Zg方向。对于给定的单元,工具路径-网格交叉点模块计算工具路径交叉点的数量m,每个交叉点的体积分数vf。体积分数等于z平面(由沿该路径运动的无限直线定义)以下部分单元的体积与单元总体积的比值。该模块还计算面积A;z平面与单元的交叉部分的中心的坐标Xa,参考于单元参考坐标系,以及面积分数af(对于每个交叉,在z平面下的所有边(i=1到单元边面的数量))。
4盒子形状工具路径-网格交叉
当工具的动作最好描述为空间变化分布的情形时,盒子形状功能是最适合的。例子包括建模Goldak的双椭球热源和聚合物挤压材料沉积时使用细网格。
一个盒子的工具路径和一个网格的交叉可以使用两种不同的算法或方法计算;即子分段法和子单元法。对于子分段和子单元方法,可以将局部xl方向的盒子长设置为0,以获得长方形的工具路径。
4.1使用子分段方法
图1描述了使用子分段方法,盒子工具路径与有限元单元E的交叉。使用依附在一个沿着路径连接点(X1,X2,X3……)的参考点(例如时间Ti时的参考点Xi)上的盒子定义工具路径。使用矢量x1,y1,z1定义一个特定分段的局部坐标系。矢量1沿着连接两个连续点的分段,z1是一个用户指定的矢量。局部坐标系的原点是分段的起始点。盒子沿着局部坐标系方向定位,中心位于分段参考点固定用户指定的偏离F。盒子被分割成用户指定数量的小盒子。假设子分段从每个小线段的中心开始,并与主线段平行。用户定义的权重与每个子段相关联。权重值与与主线段相关的字段相乘,得到与子线段相关的字段。所有子线段的权值之和通常等于1。对于给定的单元,工具路径-网格交叉模块计算子线段与该单元的交叉点数量,以及每个交叉点的起始点和结束点的坐标(ξs和ξe分表表示单元的参考坐标系)以及起始和结束时间(分别是ts和te)。

4.2使用子单元方法
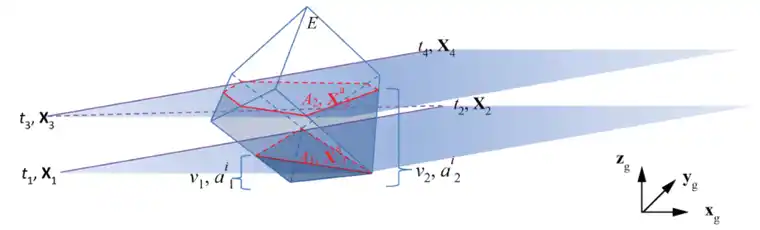
在子单元方法中,盒子不被分割成小盒子。而是,单元按照相同的拓扑分割成子单元(如图2)。模块根据单元的大小和盒子的最小尺寸自动设置单元分割成的子单元的数量。工具路径-网格交叉模块计算中心位于盒子路径内的子单元的数量、子单元中心的坐标、子单元的体积,以及盒子通过子单元中心的开始和结束时间。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删