Abaqus线性动力学分析：频率响应研究

前言：

藉由共振頻率的提取，可以初步評估結構動態行為。如果荷載是以简谐運動的方式施加，初期會是瞬态响应，但是穩定後會以简谐方式呈現。頻率响应分析即是計算掃頻區間內，改變荷載頻率探討其對結構的影响。延續兩層三跨屋架的例子，常見的荷載形式有兩種，分別為人群在樓板上跳舞以及工機具的振動，本文說明如何在提取共振頻率後，進行頻率响应分析。

模型說明：

模型設定及提取共振頻率請參考前一篇「Abaqus線性動力分析－提取共振頻率」，在此不贅述，直接進行頻率响应分析的相關設定。如下圖紅色標記處，考慮樓板上正在舉行舞會，並評估其對結構之影響。

分析步設定：

接續在提取共振頻率之後，新增 Steady-State dynamics, Modal 分析步。

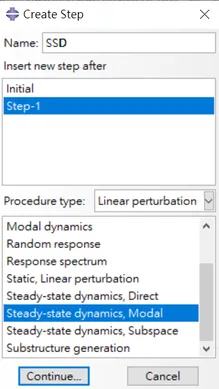
Steady-State dynamics, Modal 是基於提取共振頻率得到的振態進行疊加來求解，其優勢為速度快，缺點為不適用大阻尼、黏彈性材料。對於大阻尼、黏彈性材料等問題，建議採用 Steady-State dynamics, Direct，此方法直接對運動方程式積分計算，能夠將振態阻尼以外形式的阻尼及黏彈性材料納入考慮，相對而言，計算時間較 Steady-State dynamics, Modal 來得慢。

Basic 頁面：

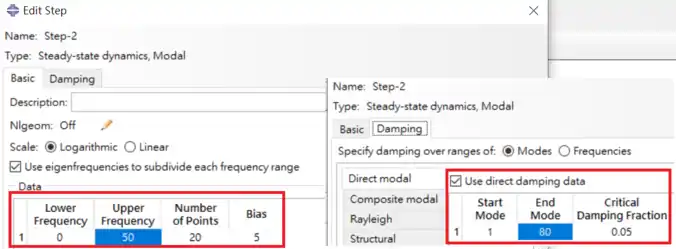
1) Scale：掃頻間隔可以為對數或是線性形式。

2) Use eigenfreq. to subdivide each frequency range：用特徵值所推算的頻率當作

間隔點，代表我們關心這些頻率點上的行為。

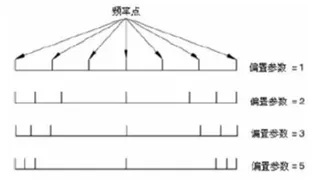
3) 輸入頻率的上下限，前述例子提取 80 個頻率後，最高頻率約為 51.057，因此這裡的區間輸入 0 至 50。Number of Points 為間隔之間打點數目，Bias 為偏置參數，如下圖所示。

Damping 頁面：

1) Specify damping over ranged of：選擇由振態或是頻率來定義阻尼比。

2) 輸入振態區間的阻尼比，前述例子提取了 80 個頻率，因此這裡定義 1 至 80個振態的阻尼比為 0.05。定義阻尼比有很多種方式，可以由振態、Rayleigh、Structural 及材料參數定義阻尼。

輸出設定：

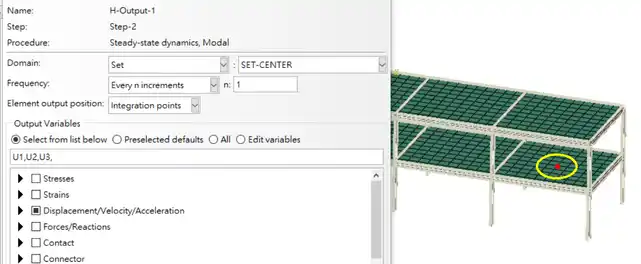
選擇樓板中央之節點建立集合，於 History Output 內輸出該集合的位移。

邊界條件設定：

1) 底部延續前一分析步之完全固定條件。

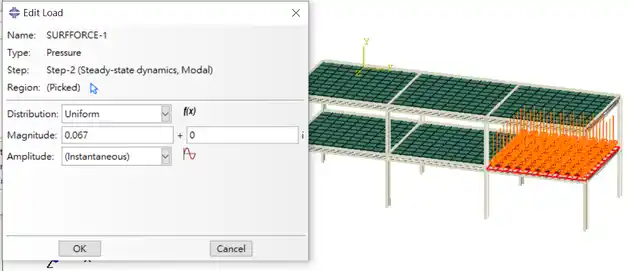
2) 考慮參加舞會的人數為 25，每位成人平均重量 70kg，計算後可得總重量為17167.5N，再轉換成英制單位 3859.41lbf.，依據樓板尺寸可計算壓力約為0.067psi，將壓力施加在樓板上，如下圖所示，將數值輸入到實部。

結果與討論：

先從 Result Options 功能內，把 Complex Form 切換成 Magnitude。

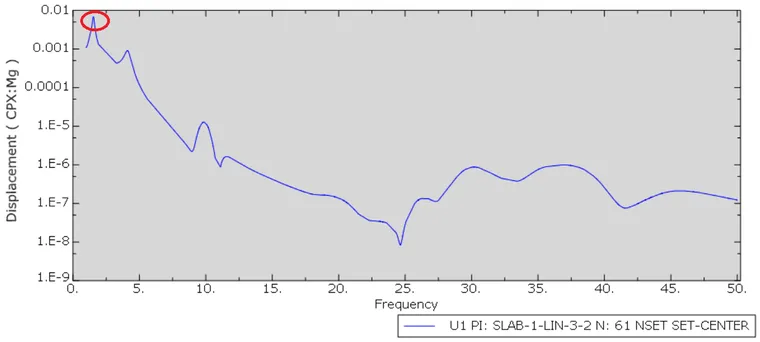
根據前面共振頻率的結果，第一個頻率主要貢獻在 x 方向，因此先觀察 U1 之結果，第一個峰值出現在頻率 1.57Hz，位移是 0.006317in，換算後約為 0.156mm，此位移量極小，不會對結構造成危害。接著觀察 U2 之結果，在頻率 9.45Hz 時有位移 0.16in，換算之後約為 4.06mm，即便此結果較 U1 大，但是未經訓練的一般民眾，要將舞步採到每秒 9 步是有難度，因此可以忽略此情況造成的影響。

延伸討論：

在線性動力學的範疇內，輸入與輸出為比例關係。如考慮小型機具運轉對樓房造成的影響，假設機具重量為350kg，為先前求得人群總重1750kg的0.2倍，機具穩定转速為3000rpm (50Hz)，可以根據U1在靠近50HZ的結果1.23E-7 in乘以倍率0.2，再換算得到3.12E-6 mm，因此在本問題中，機具運轉對樓房的影响極小，不足以構成危害。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删