非等温线弹性UMAT子程序实现与Abaqus内部机制解析

将拉梅常数看做是温度的函数，则非等温弹性张量方程为：

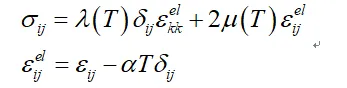
其中，l和m是拉梅常数，a是线膨胀系数，T是温度。对方程两边取材料时间导数，得到Jaumann率形式：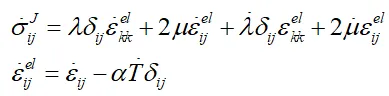

写成增量形式为：

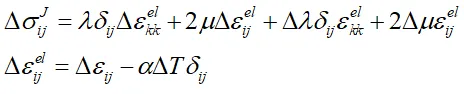
Abaqus Standard采用增量法逐步施加载荷/位移，每步增加的应力即可按上式进行计算。材料的切线刚度矩阵（雅克比矩阵）为应力对应变的偏导数，采用voigt记法写成6*6的二维矩阵为（引用知乎@Learning STRB）：

简单介绍了一下理论，下面是UMAT程序：

     SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,

    1 RPL,DDSDDT,DRPLDE,DRPLDT,

    2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,

    3 NDI,NSHR,NTENS,NSTATEV,PROPS,NPROPS,COORDS,DROT,PNEWDT,

    4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,KSTEP,KINC)

C

     INCLUDE 'ABA_PARAM.INC'

C

     CHARACTER*8 CMNAME

     DIMENSION STRESS(NTENS),STATEV(NSTATEV),

    1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),

    2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),

    3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3)

C     LOCAL ARRAYS

C     ----------------------------------------------------------------

C     EELAS - ELASTIC STRAINS 弹性应变（不含热应变）

C     ETHERM - THERMAL STRAINS 热应变

C     DTHERM - INCREMENTAL THERMAL STRAINS 增量热应变

C     DELDSE - CHANGE IN STIFFNESS DUE TO TEMPERATURE CHANGE 雅克比矩阵增量

C     ----------------------------------------------------------------

     DIMENSION EELAS(6), ETHERM(6), DTHERM(6), DELDSE(6,6)

C

     PARAMETER(ZERO=0.D0, ONE=1.D0, TWO=2.D0, THREE=3.D0, SIX=6.D0)

C     ----------------------------------------------------------------

C     UMAT FOR ISOTROPIC THERMO-ELASTICITY WITH LINEARLY VARYING

C     MODULI - CANNOT BE USED FOR PLANE STRESS

C     ----------------------------------------------------------------

C     PROPS(1) - E(T0)

C     PROPS(2) - NU(T0)

C     PROPS(3) - T0

C     T0温度下的弹性模量和泊松比

C     PROPS(4) - E(T1)

C     PROPS(5) - NU(T1)

C     PROPS(6) - T1

C     T1温度下的弹性模量和泊松比

C     PROPS(7) - ALPHA

C     PROPS(8) - T_INITIAL

C     线膨胀系数和参考温度

C     ELASTIC PROPERTIES AT START OF INCREMENT

C     技术邻@snowwave02 大神的方法，配合他自研的isolver求解器可以实现断点调试，这一步可以定位到第*次进入UMAT程序。

     integer,save::number=0

     number=number+1

     if(number.eq.3) then

        number1=0

     endif

C     初始温度下的拉梅常数

     FAC1=(TEMP-PROPS(3))/(PROPS(6)-PROPS(3))

     IF (FAC1 .LT. ZERO) FAC1=ZERO

     IF (FAC1 .GT. ONE) FAC1=ONE

     FAC0=ONE-FAC1

     EMOD=FAC0*PROPS(1)+FAC1*PROPS(4)

     ENU=FAC0*PROPS(2)+FAC1*PROPS(5)

     EBULK3=EMOD/(ONE-TWO*ENU)

     EG20=EMOD/(ONE+ENU)

     EG0=EG20/TWO

     ELAM0=(EBULK3-EG20)/THREE

C

C     ELASTIC PROPERTIES AT END OF INCREMENT

C     增量温度下的拉梅常数

     FAC1=(TEMP+DTEMP-PROPS(3))/(PROPS(6)-PROPS(3))

     IF (FAC1 .LT. ZERO) FAC1=ZERO

     IF (FAC1 .GT. ONE) FAC1=ONE

     FAC0=ONE-FAC1

     EMOD=FAC0*PROPS(1)+FAC1*PROPS(4)

     ENU=FAC0*PROPS(2)+FAC1*PROPS(5)

     EBULK3=EMOD/(ONE-TWO*ENU)

     EG2=EMOD/(ONE+ENU)

     EG=EG2/TWO

     ELAM=(EBULK3-EG2)/THREE

C     ELASTIC STIFFNESS AT END OF INCREMENT AND STIFFNESS CHANGE

C     求解雅克比矩阵和雅克比矩阵的增量（简单说是T1温度和T0温度的雅克比矩阵差值）

     DO K1=1,NDI

     DO K2=1,NDI

     DDSDDE(K2,K1)=ELAM

     DELDSE(K2,K1)=ELAM-ELAM0

     END DO

     DDSDDE(K1,K1)=EG2+ELAM

     DELDSE(K1,K1)=EG2+ELAM-EG20-ELAM0

     END DO

     DO K1=NDI+1,NTENS

     DDSDDE(K1,K1)=EG

     DELDSE(K1,K1)=EG-EG0

     END DO

C

C     CALCULATE THERMAL EXPANSION

C     计算热膨胀应变和热膨胀应变的增量（热应变仅有主应变，没有切应变）

     DO K1=1,NDI

     ETHERM(K1)=PROPS(7)*(TEMP-PROPS(8))

     DTHERM(K1)=PROPS(7)*DTEMP

     END DO

      DO K1=NDI+1,NTENS

     ETHERM(K1)=ZERO

     DTHERM(K1)=ZERO

     END DO

C

C     CALCULATE STRESS, ELASTIC STRAIN AND THERMAL STRAIN

C     按应力的增量公式计算应力增量，进而计算应力。

     DO K1=1, NTENS

     DO K2=1, NTENS

     STRESS(K2)=STRESS(K2)+DDSDDE(K2,K1)*(DSTRAN(K1)-DTHERM(K1))

    1 +DELDSE(K2,K1)*( STRAN(K1)-ETHERM(K1))

     END DO

     ETHERM(K1)=ETHERM(K1)+DTHERM(K1)

     EELAS(K1)=STRAN(K1)+DSTRAN(K1)-ETHERM(K1)

     END DO

C

C     STORE ELASTIC AND THERMAL STRAINS IN STATE VARIABLE ARRAY

C     存储弹性应变至状态变量SDV1-SDV12

     DO K1=1, NTENS

     STATEV(K1)=EELAS(K1)

     STATEV(K1+NTENS)=ETHERM(K1)

     END DO

     RETURN

     END

建立单个单元的热力耦合有限元模型。

有限元材料参数为（Model-1）：E(T0)=200GPa，NU(T0)=0.3，T0=293K；E(T1)=300GPa，NU(T1)=0.3，T1=393K；ALPHA=1e-5，T_INITIAL=293K。另外设置密度、比热容、热导率。为了排除传热因素的影响，我在后续载荷步里采用直接指定温度的方法，因此上述参数可任意设置。

作为对照，采用Abaqus自带的材料设置Model-2：

几何模型为1m*1m*1m的立方体，采用C3D8T绘制1个单元。

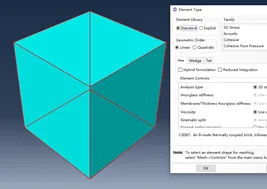
设置两个分析步：初始状态设置域温度为293K；分析步1约束X负方向上四个节点X方向位移，X正方向上四个节点加载X方向位移0.1m；分析步2设置整个域温度为393K。

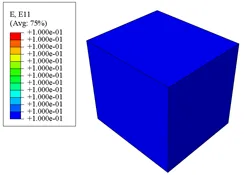
经过对比，Model-1和Model-2的计算结果完全一致。下面仅展示Model-1的计算结果：前两个图是分析步1的X方向应力和总应变，后图为分析步2的X方向应力和弹性应变（采用位移加载，分析步2的总应变不变）。

下面对计算结果进行讨论。笔者经过有限元计算，如果不考虑热膨胀，分析步2计算完成后应力为3e10Pa。由于自由热膨胀不产生应力，因此线膨胀系数的引入造成了应力的减小。

特别注意的是，在有限元建模过程中，自定义的材料并未使用Abaqus自带的热膨胀项，完全是通过编写的UMAT来计算材料的热膨胀贡献。那么，如果我们额外增加Abaqus自带的热膨胀项（材料属性里的expansion项），那么弹性应变会变为0.098，应力为变为2.94e10MPa。也就是说我们计算了两次热膨胀系数。笔者做出了如下猜想：一旦设置了热膨胀属性，进入Abaqus的应变就从总应变张量变为了弹性应变张量。因此，如果需要编写含温度参数的UMAT子程序，我们要么使用Abaqus自带的expansion项，要么在UMAT中将热膨胀贡献考虑，切勿重复。

上述讨论仅针对了应变和应变增量，许多本构模型采用的是变形梯度描述的，后续有时间笔者会对此再做一次验证。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删