ABAQUS网格控制全解析：三种网格划分技术详解

ABAQUS网格控制属性详解（三种网格划分技术）

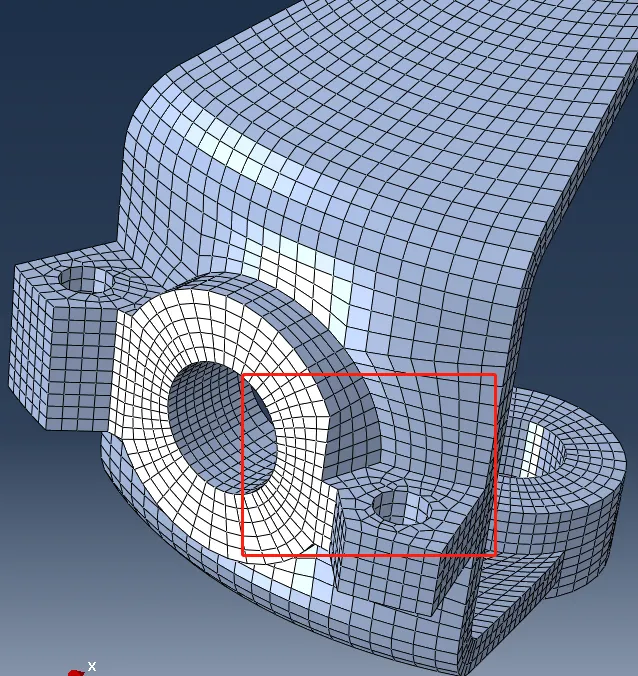
理解ABAQUS中重要的网格划分工具原理，尤其是理解ABAQUS里面的网格控制属性设置，这对于复杂网格划分尤其有用。

如图1，是ABAQUS中网格控制属性中的网格划分“技术”选项，它ABAQUS是决定采用何种策略划分网格的选项。

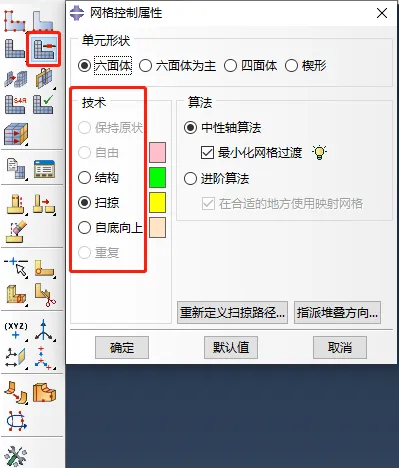
图1 ABAQUS网格控制属性对话框

这几个选项看着挺简单，却很重要。然而，关于这里的ABAQUS网格划分“技术”的解读，恰恰是很多教程缺失的内容。理解这背后的技术原理直接影响着我们对复杂实体网格划分的切分策略！

ABAQUS重要而常用的三种“自顶向下”的网格划分技术是：自由网格技术、结构网格技术、扫掠网格技术。

1）自由网格技术，对于二维面几何来说，任何形状的面都能选择四边形、四边形为主和三角形；对于三维实体几何，只能生成四面体网格。这很简单，如图2所示。

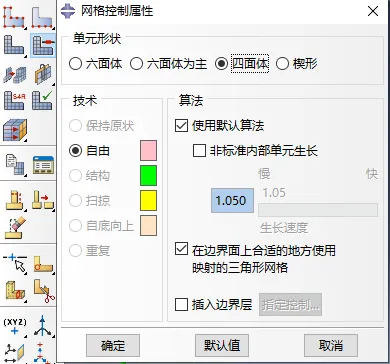
图2 ABAQUS自由网格划分技术

2）在ABAQUS的网格划分技术中，扫掠网格技术扮演着十分重要的角色。首先是来自官方《ABAQUS文档》中的定义（翻译）：扫掠网格先创建源网格，然后沿着扫掠路径的边，一次次地拷贝源网格节点，直到到达目标区域；后边还补充说明，如果扫掠路径的边是直线或样条线，称为拉伸扫掠，如果扫掠路径是圆（弧）线称为旋转扫掠。这个定义显得有些笼统。然而我们在实际使用中已经知道，这里的所谓“拷贝”是广义的，这里的所谓“沿着一条路径”也是广义的。

《ABAQUS文档》中分为二维和三维的场景，讨论了哪些形状可以扫掠，哪些形状不可以，这些内容才是对我们划分网格有指导意义的。

注意一个重要的要求是：对三维实体，目标面必须是单一的面。这里我们引用ABAQUS官方文档的图例简单解释，如图3，图左边可以，而右边不行。

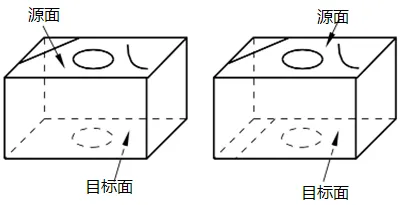
图3 ABAQUS扫掠网格的源面和目标面

然而上述这个事实却不是针对曲面网格的，针对曲面网格必须是四边形才能做扫掠网格（并且不管四边形的边是直边还是曲边）；而曲面网格对划分结构网格的几何要求反而放得更松一些，实际上，只要没有孔，几乎所有的连续面都可以是结构网格，有孔也没关系，做一下切分就可以。这一事实似乎有些反常规认识。但是，由于二维网格的简单性，这些概念上的困扰几乎没有影响到我们的工作。ABAQUS文档中把这个事情描述得稍微复杂，我们这里放上几个例图看，不作过多解释。

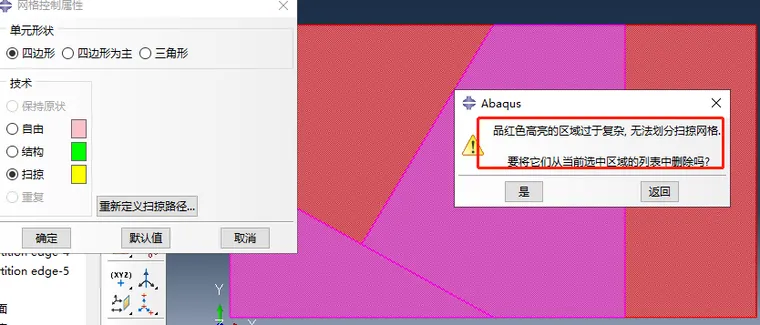
图4 三角形和五边形可以划分结构网格，但不能划分扫掠网格

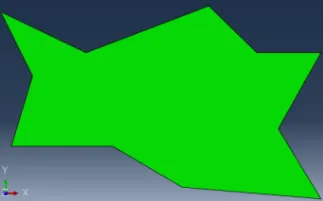
图5 这样的任意多边形可以划分结构网格，但不能划分扫掠网格

图6 曲边的四边形能划分扫掠网格，也能划分结构网格

我们继续来讨论三维情况的扫掠。关于扫掠网格的连接源面和目标面的侧面，要求：它们或者是单一的表面；或者表面由四边形面组成，并且这些四边形是呈行列布置的。引用文档中的例子如图7和图8，图7是允许的情况，图8是不允许的情况（图8的右图的四边形不是行列布置）。

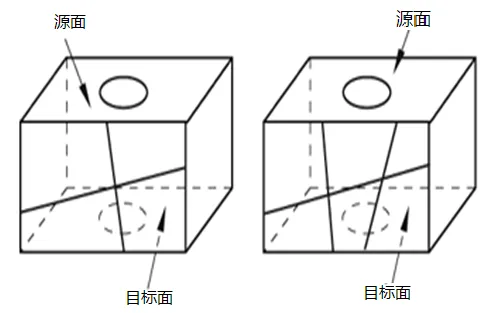
图7 允许扫掠网格

图8 不能生成扫掠网格

在早期版本的文档中提到，旋转轴上是一个尖点的旋转体不能生成扫掠网格，如图9所示。目前这个规则仍然有效。容易理解，在尖点位置是个五面体金字塔形状，而ABAQUS里没有金字塔单元。这种情况只能切一部分出来做四面体单元；或者把金字塔分成两个四面体几何形状（后面我们即将要讨论结构网格技术时也将谈到：ABAQUS中，一个四面体几何形状可以划分结构化的全六面体三维网格！）。

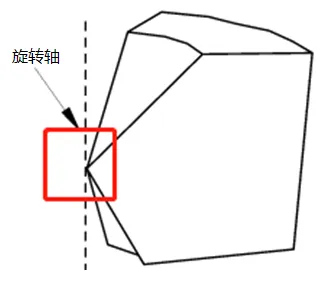
图9 尖点不可做扫掠网格

类似地，实心的旋转体（如实心轴）可以作旋转扫掠，但中心是楔形单元。如图10所示。当然楔形单元没问题，也可以通过切分修改扫掠方向为轴向，此时的阶梯轴必须从阶梯位置断开，这样可以在轴的圆截面上划分自由四边形网格或者在圆截面上画分割线（比如蝶形网格样式的线）来改善单元形状。

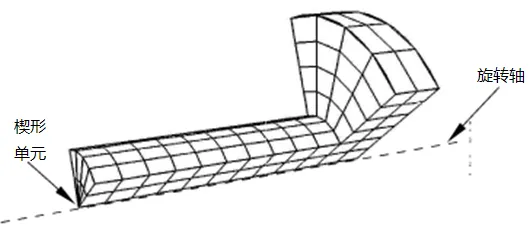
图10 实心旋转体扫掠网格

还有就是，文档中提到，类似于图11这种复杂的图形也是可以生成扫掠网格的。理由是：源面虽然是两个，但目标面只有一个，而且各个连接面都是单一的表面。

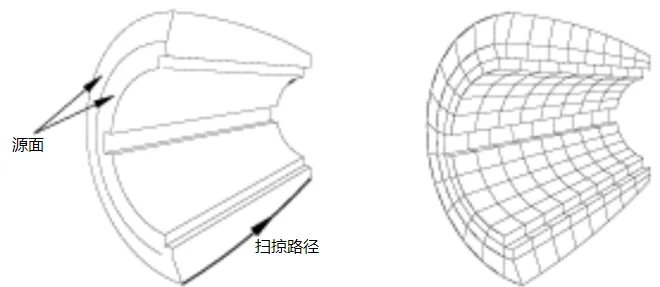
图11看起来复杂却可以生成扫掠网格的例子

另外，利用虚拟拓扑工具合并目标面，使得满足扫掠网格划分的要求。这种利用虚拟拓扑合并面或者忽略边来满足扫掠网格划分要求的手法是我们经常需要用到的技术。

关于扫掠网格，有一个经典的例子：它是关于多个源面的夹角问题。ABAQUS要求（多个）源面之间的夹角是“接近”180°的。如图12所示，左边是可以生成扫掠网格的，而右边是不可以的。像这种形状类似的几何体，网格划分却存在巨大区别。它们与尺寸相关，尤其是角度尺寸相关。这样的例子在实际项目中经常会遇到。

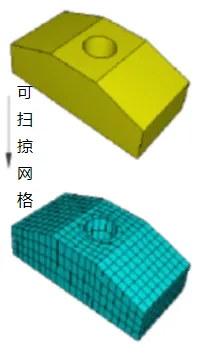
图12 与角度相关的源面

但是，如图13右图所示，可以通过虚拟拓扑连接面来实现扫掠网格。通过虚拟拓扑操作，把三个面合并，当作一个面，自然就忽略了角度问题，但划分出的网格在原来连接边线上往往比较难看。

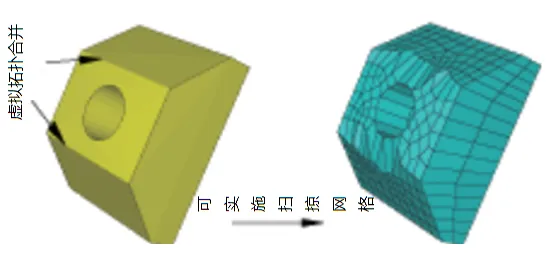
图13 通过虚拟拓扑实现扫掠网格划分

对于欲划分六面体网格的工作来说，我们打交道最多的就是扫掠网格，其次才是结构网格。从概念上来说，三维情况的结构网格相对清楚简单一些，但也有些反常识的特例！这些特例对某些特殊情况特别重要！

3）ABAQUS的三维实体的结构化网格在网格划分中同样扮演着十分重要的角色。由于结构网格的重要特性，它们在一些关键连接位置有着重要作用。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删